3.Используя теорему Остроградского-Гаусса, получить формулу для расчета напряженности в произвольной точке поля заряда q равномерно распределенного по поверхности сферы.
6 Дифференциальная форма теоремы остроградского- гаусса
Пусть в некоторой области пространства известна объемная плотность зарядов x,y,z и эта функция непрерывна аналогично представлению о непрерывном распределении вещества.
Рассмотрим в этом пространстве вблизи некоторой точки с координатами x,y,z настолько малый объем dV=dx·dy·dz, что объемная плотность зарядов в нем практически постоянна. Тогда заряд этого объема равен dq=(x,y,z)·dV
Найдем поток через поверхность граней перпендикулярных оси ОХ:
Аналогично можно рассчитать поток через две пары других оснований.
Тогда поток через поверхность всех граней объема:
РИС.17
-
Физический смысл дивергенции вектора напряженности в том, что она равна числу линий напряженности выходящих (входящих) из единичного объема, т.е. характеризует расходимость (сходимость) линий напряженности.
Согласно теореме Остроградского-Гаусса
в интегральной форме:
,
- дифференциальная форма теоремы
Остроградского-Гаусса.
Эта форма применима лишь при условии, если объемная плотность зарядов конечная величина, является следствием интегральной формы и констатирует, что заряды являются источниками (стоками) линий вектора напряженности.
Если ввести векторный оператор Гамильтона:
,
Можно записать :
§7 Работа сил электростатического поля по перемещению заряда. Теорема о циркуляции вектора напряженности.
Под действием сил электрического поля свободный пробный заряд начинает двигаться. Рассмотрим поле положительного точечного заряда, в котором под действием сил поля пробный заряд переместился из точки 1 в точку 2.
Проведем радиусы-векторы от заряда, создающего поле, в эти точки. Так как поле неоднородное и сила, действующая на пробный заряд, не постоянна, то найдем работу на малом перемещении:
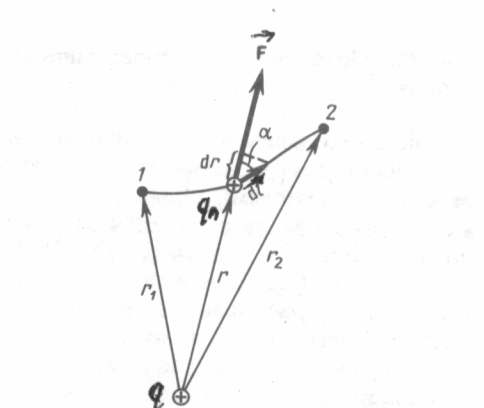
РИС.18
Следовательно, работа сил электростатического поля не зависит от формы траектории, а определяется только начальным и конечным положением пробного заряда.
Поле, работа сил которого не зависит от траектории, называется потенциальным.
Отсюда следует, что если пробный заряд будет перемещаться по замкнутой траектории, то суммарная работа будет равна нулю:
Если поле создается несколькими точечными зарядами, то работу по перемещению пробного заряда можно рассчитать, используя принцип суперпозиции:
Следовательно, любое электростатическое поле потенциально.
Учитывая, что в этом случае:
,
Тогда при перемещении по замкнутой траектории:
Поскольку qn=0 не имеет смысла, то для любого потенциального поля:
- теорема о циркуляции вектора
напряженности.
Циркуляция вектора напряженности электростатического поля по любому замкнутому контуру равна нулю.
Следствием теоремы является то, что линии напряженности электростатического поля не могут быть замкнуты.
Теорема о циркуляции является критерием потенциальности поля.