§ 55.Вынужденные электромагнитные колебания. Резонанс напряжений.

Как уже обсуждалось в § 50, рассмотренная цепь из последовательно соединенных индуктивности, емкости и активного сопротивления может рассматриваться как колебательная система, так как в ней возможно возникновение электромагнитных колебаний с собственной частотой

при .

Эти колебания являются затухающими, так как энергия, сосредоточенная в контуре в момент возникновения колебаний выделяется в виде тепла на активном сопротивлении во время колебательного процесса.

Тогда, при включении в контур источника переменной ЭДС, его можно рассматривать как элемент, инициирующий в контуре вынужденные колебания с частотой . Следовательно, уравнение

представляет собой уравнение вынужденных электромагнитных колебаний под действием внешней периодически изменяющейся ЭДС.

Используя введенные в § 50 физические величины: собственную частоту и коэффициент затухания это уравнение можно представить и в виде .

Как известно, для вынужденных колебаний характерно явление резонанса, которое заключается в возрастании амплитуды вынужденных колебаний при приближении частоты внешнего воздействия к резонансной частоте, зависящей от параметров колебательной системы.

В рассматриваемой цепи - колебательном контуре вынужденные колебания совершают сила тока, заряд и напряжение на конденсаторе, а также напряжение на катушке индуктивности.

Резонансными кривыми называются зависимости амплитудных значений, совершающих вынужденные колебания физических величин, от частоты внешнего воздействия, т.е., в нашем случае, от частоты источника ЭДС.

Закон Ома для рассматриваемой цепи – колебательного контура позволяет проанализировать зависимость амплитуды силы тока от частоты источника ЭДС: .

Если амплитудное значение ЭДС, а также величины активного сопротивления, емкости и индуктивности постоянны, то амплитудное значение силы тока зависит только от частоты.

Максимальная амплитуда силы тока: при . В этом случае частота источника ЭДС совпадает с собственной частотой колебательного контура: ,

т.е. для вынужденных колебаний силы тока наблюдается резонанс.

На рис.155 показаны резонансные кривые для амплитуды силы тока в зависимости от частоты источника при различном активном сопротивлении колебательного контура. Резонанс выражен тем отчетливее, чем меньше активное сопротивление, т.е. чем меньше коэффициент затухания .

Колебания заряда и напряжения на конденсаторе совпадают по фазе. Найдем зависимость амплитуды колебаний заряда от частоты. Как показано в § 51 . Если использовать выражения для собственной частоты и коэффициента затухания, то это выражение преобразуется к виду:

. Максимальное значение амплитуды заряда достигается при минимальном значении подкоренного выражения. Возьмем производную от подкоренного выражения по частоте и приравняем ее нулю: или . Подставив это значение в выражение для амплитудного значения заряда, получим: .

Так как , то максимальная амплитуда напряжения на конденсаторе достигается при том же значении частоты источника ЭДС: .

На рис.156 и рис.157 показаны резонансные кривые для амплитудных значений заряда и напряжения на конденсаторе при различных активных сопротивлениях контура.

Резонансная частота для заряда и напряжения всегда меньше, чем резонансная частота для тока, а резонанс выражен тем больше, чем меньше активное сопротивление контура.

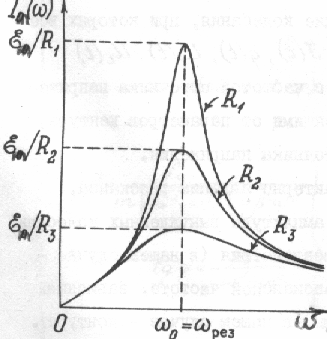
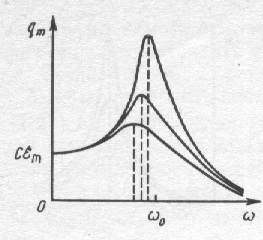
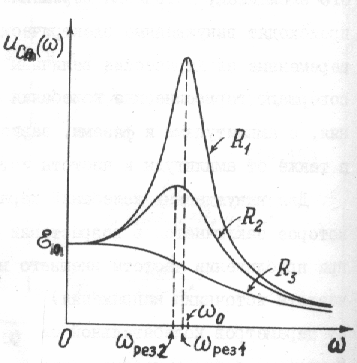
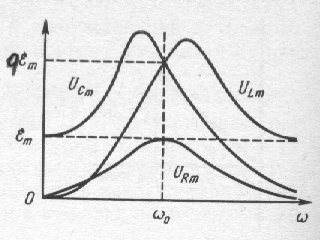
РИС.155 РИС.156 РИС.157 РИС.158

Максимальное значение напряжения на катушке индуктивности (см.§ 51) преобразуем также, используя понятия собственной частоты и коэффициента затухания:

. Резонансную частоту можно найти, взяв производную по частоте от этого выражения и приравняв ее к нулю. Резонансная частота для напряжения на катушке индуктивности равна: .

Если преобразовать и сравнить выражения для резонансных частот на конденсаторе и на катушке индуктивности с резонансной частотой тока: , , , то можно сделать вывод, что , общем случае, резонансная частота для напряжения на конденсаторе всегда меньше, а для напряжения на катушке индуктивности всегда больше, чем резонансная частота для силы тока (и напряжения на активном сопротивлении). Резонансные кривые для напряжений на активном сопротивлении, катушке индуктивности и емкости показаны на рис.158.

Для представляющих практический интерес контуров с малым затуханием, , членом можно пренебречь. В этом случае резонанс для всех переменных электрических величин: силы тока, заряда и напряжения на конденсаторе, напряжения на катушке индуктивности наступает практически одновременно при частоте источника, равной частоте свободных колебаний в контуре:

. При резонансе сдвиг фаз между током и напряжением равен нулю (рис.159).

Для контуров с большим затуханием, если активное сопротивление так велико, что , подкоренное выражение становится мнимым и резонансная кривая не имеет максимума, т.е. резонанс отсутствует. В этом случае, зависимость, например, напряжения на конденсаторе от частоты источника представлена на рис.157 для сопротивления R₃.

Рассмотренное явление резонанса при последовательном соединении источника с элементами контура называется резонансом напряжений. При этом - называется волновым или характеристическим сопротивлением, а максимальные напряжения на катушке индуктивности и конденсаторе равны и противоположны по фазе.

Для контуров с малым затуханием характерен «острый» резонанс и высокая добротность , которая (см.§ 50) характеризует относительную убыль энергии контура за период при свободных колебаниях.

Физический смысл добротности для контуров с малым затуханием при резонансе.

1)Добротность показывает во сколько раз максимальное значение амплитуды напряжения на конденсаторе (и на индуктивности) превышает амплитуду внешней ЭДС (рис.158). .

Следовательно, необходимо учитывать, что при резонансе, даже при небольшой внешней ЭДС, напряжения на индуктивности и емкости могут достигать большой величины, опасной для жизни человека:

2)Можно показать, что добротность характеризует относительную ширину резонансной кривой: . Шириной резонансной кривой, или полосой пропускания называется интервал частот , ограниченный частотами и , на которых амплитуда в меньше амплитуды при резонансе (рис.160).

Следовательно, добротность – величина обратная относительной ширине пропускания или относительной ширине резонансной кривой.

Резонанс используется для выделения из сложного «сигнала» (зарегистрированного напряжения) нужной составляющей. Это имеет практическое значение в радиотехнике при приеме и настойке на определенную частоту радиосигнала. Чем выше добротность контура, тем уже резонансная кривая и тем легче «отстраиваться» от передач, ведущихся на соседних частотах.

На практике добротность контура подбирается и с учетов необходимого качества приема сигнала, так как с уменьшение ширины резонансной кривой уменьшается информация (диапазон частот) «пропускаемый» контуром.

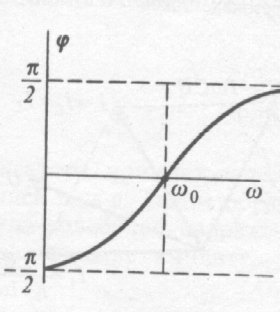
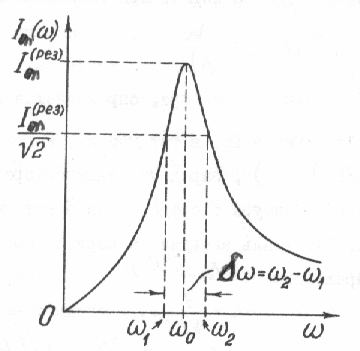
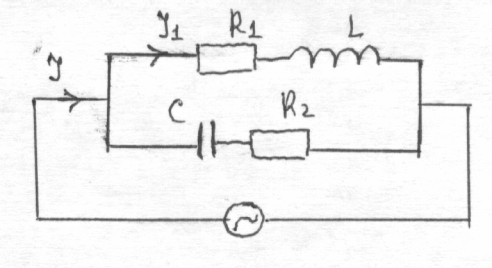
РИС.159 РИС.160 РИС.161