
- •2)Гипотеза кварков.
- •2)Почему трением электризуются только разнородные вещества?
- •3)Почему трением практически невозможно наэлектризовать проводники? §2.Закон кулона
- •§3. Напряженность электростатического поля. Полевая трактовка закона кулона. Принцип суперпозиции.
- •§4 Линии вектора напряженности. Поток вектора напряженности.
- •2)Изобразить поле двух равных по величине положительных точечных зарядов;
- •4)Изобразить качественно поле:
- •§5 Теорема остроградского-гаусса.
- •3.Используя теорему Остроградского-Гаусса, получить формулу для расчета напряженности в произвольной точке поля заряда q равномерно распределенного по поверхности сферы.
- •6 Дифференциальная форма теоремы остроградского- гаусса
- •§7 Работа сил электростатического поля по перемещению заряда. Теорема о циркуляции вектора напряженности.
- •§8. Разность потенциалов, потенциал электростатического поля.
- •§9 Связь напряженности и разности потенциалов.Эквипотенциальные поверхности.
- •§11 Поле электрического диполя.
- •Тема II. Электростатическое поле при наличии проводников. §12 электрическое поле заряженного проводника.
- •13. Электростатическая индукция.
- •§14 Электрическая емкость уединенного проводника и системы проводников.
- •Тема III. Электрическое поле при наличии диэлектриков. §15 классификация диэлектриков.
- •§ 16 Диполь в электрическом поле.
- •17. Вектор поляризации и связанные заряды.
- •§ 18. Теорема остроградского – гаусса для вектора напряженности в диэлектриках. Вектор электрического смещения.
- •§ 19. Диэлектрическая восприимчивость и диэлектрическая проницаемость.
- •§ 20 Граничные условия.
- •§ 21 Сегнетоэлектрики.
- •Тема IV. Энергия электростатического взаимодействия. §22.Энергия взаимодействия системы неподвижных точечных зарядов.
- •§23 Энергия непрерывно распределенных зарядов, энергия заряженного проводника, конденсатора.
- •§ 24 Энергия электростатического поля, энергия взаимодействия заряженных тел.
- •Тема V. Стационарный электрический ток. § 25. Сила и плотность тока.
- •26. Уравнение непрерывности.
- •§ 27. Экспериментальные законы стационарного тока.
- •§ 28 Законы ома и джоуля – ленца в дифференциальной форме.
- •§ 29. Условия существования стационарного тока. Электродвижущая сила.
- •§ 30. Поле постоянного тока.
- •§ 31. Закон ома для замкнутой цепи.
- •§ 32. Правила кирхгофа для линейных разветвленных цепей.
- •§ 33. Квазистационарные токи.
- •Тема VI. Магнитное поле стационарного тока в вакууме. § 34. Закон взаимодействия элементов тока. Вектор магнитной индукции.
- •§ 35. Закон ампера. Сила лоренца.
- •§ 36 Линии вектора магнитной индукции. Теорема о полном магнитном потоке.
- •§ 37. Теорема о циркуляции вектора магнитной индукции. Вихревой характер магнитного поля.
- •§ 38.Контур с током в магнитном поле.
- •Тема VII. Магнитное поле в веществе. § 39. Источники магнитного поля в веществе. Вектор намагничивания.
- •§ 40. Связь молекулярных токов с вектором намагничивания.
- •§ 41. Теорема о циркуляции вектора магнитной индукции в магнетиках. Напряженность магнитного поля.
- •§ 42 Магнитная восприимчивость. Магнитная проницаемость. Источники линий напряженности.
- •§ 43. Граничные условия для векторов напряженности и магнитной индукции.
- •Тема VIII. Нестационарное магнитное поле. § 44. Явление электромагнитной индукции.
- •§ 45 Природа сторонних сил при явлении электромагнитной индукции.
- •§ 46. Явление самоиндукции.
- •§ 47. Взаимная индукция.
- •§ 48 Энергия магнитного поля.
- •Тема IX. Цепи переменного тока. § 49. Колебательный контур. Свободные элетромагнитные колебания в идельном контуре.
- •§ 50 Свободные колебания в контуре с активным сопротивлением.
- •§ 51. Цепь переменного тока с различной нагрузкой.
- •§ 52 Последовательная цепь переменного тока со смешанной нагрузкой.
- •§ 53. Энергия и мощность в цепи переменного тока.
- •§ 54 Разветвленная цепь переменного тока. Метод проводимостей.
- •§ 55.Вынужденные электромагнитные колебания. Резонанс напряжений.
- •§ 56 Резонанс токов.
- •§ 57.Трехфазный ток.
- •Тема X. Магнетики § 58 магнитомеханические явления.
- •§ 59 Диамагнетизм. Ларморова прецессия.
- •§ 60 Парамагнетики.
- •Самостоятельно: §61 ферромагнетики. Тема XI. Электромагнитное поле § 62 . Обобщения максвелла. Ток смещения.
- •§ 63 Полная система уравнений максвелла. Теория максвелла и границы ее применимости.
- •§ 64. Электромагнитные волны и их свойства.
- •§ 65. Закон сохранения энергии электромагнитного поля. Поток энергии.
- •§ 66. Излучение электромагнитных волн.
- •§ 67 Экспериментальные подтверждения теории максвелла: опыты герца и лебедева.
- •Тема XII. Электропроводность веществ. § 68. Классическая теория электропроводности металлов (друде-лоренца) и ее затруднения.
- •§69.Основные понятия зонной теории проводимости твердых тел.
- •§ 70 Собственная и примесная проводимость полупроводников,
- •§ 71 Работа выхода. Контактные явления в металлах.
- •§ 72 Контакт полупроводников с различным типом проводимости.
- •§ 73 Термоэлектрические явления.
§ 52 Последовательная цепь переменного тока со смешанной нагрузкой.
Рассмотрим участок цепи, состоящий из последовательно соединенных активного сопротивления, конденсатора емкостью С и катушки с индуктивностью L (рис.139), по которому течет ток .
В случае квазистационарного тока, согласно закону сохранения энергии, общее мгновенное напряжение на этом участке будет складываться из мгновенных напряжений на каждом из последовательно включенных элементов:
![]() .
.
Так как складываемые напряжения представляют собой гармонические колебания одной частоты, то и мгновенное напряжение также будет изменяться с такой же частотой.
Рассчитать амплитудное значение этого напряжения и сдвиг фаз по отношению к силе тока можно двумя способами: используя тригонометрические формулы для суммы и разности или методом векторных диаграмм (рис.140). Воспользуемся методом векторных диаграмм.
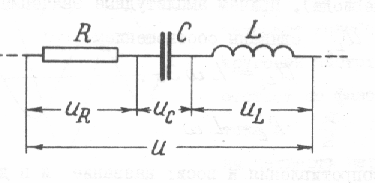
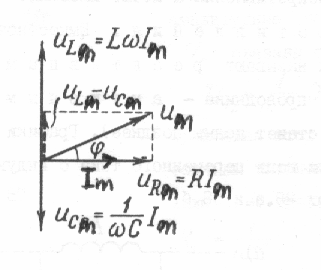

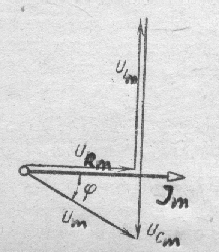
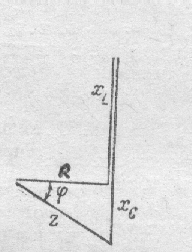
РИС.139 РИС.140 РИС.141 РИС.142 РИС.143
Построив вектор-амплитуду
результирующего напряжения как векторную
сумму амплитуд напряжений на всех
элементах, получим:
![]()
Следовательно, и в случае смешанного
последовательного соединения различных
нагрузок, амплитудные значения силы
тока и общего напряжения связывает
соотношение аналогичное закону Ома:
![]() ,
где
,
где
![]() представляет собой полное сопротивление
(импеданс) данного участка цепи.
представляет собой полное сопротивление
(импеданс) данного участка цепи.
Как видно из рис.140, суммарное
мгновенное напряжение сдвинуто по фазе
относительно силы тока и изменяется
соответственно по закону
![]() .
Сдвиг фаз можно определить с помощью
векторной диаграммы:
.
Сдвиг фаз можно определить с помощью
векторной диаграммы:
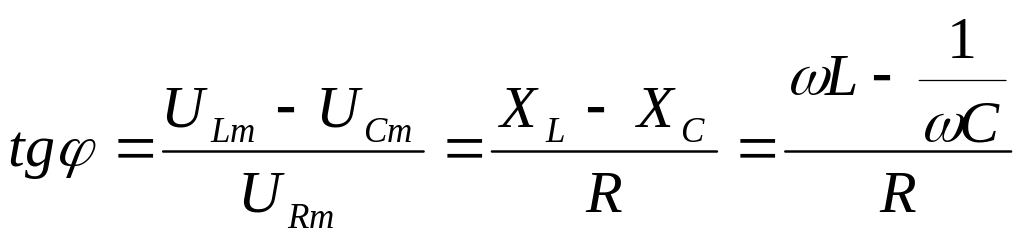 .
Из этой формулы следует, что в зависимости
от соотношения индуктивного и емкостного
сопротивлений участка цепи общее
мгновенное напряжение может как
опережать, так и отставать по фазе от
мгновенной силы тока.
.
Из этой формулы следует, что в зависимости
от соотношения индуктивного и емкостного
сопротивлений участка цепи общее
мгновенное напряжение может как
опережать, так и отставать по фазе от
мгновенной силы тока.
Важно отметить, что, хотя мгновенные значения напряжений складываются, полное сопротивление цепи не является арифметической суммой активного, емкостного и индуктивного сопротивлений.
Разность индуктивного и емкостного
сопротивлений называется реактивным
сопротивлением цепи:
![]() .
.
Эта величина может быть положительной или отрицательной, что по физическому смыслу будет определять опережение или отставание по фазе напряжение от силы тока в цепи. Следствием последовательного соединения элементов цепи и векторной диаграммы напряжений является «треугольник» сопротивлений.
Полное сопротивление в этом прямоугольном треугольнике представляет собой гипотенузу, а катеты – это активное и реактивное сопротивления.
На рис. 141 треугольник сопротивлений в цепи с положительным реактивным сопротивлением. На рис.142 и рис.143 показаны векторная диаграмма и треугольник сопротивления для цепи «емкостного» характера, т.е. реактивное сопротивление в этом случае отрицательно.
На рис.144 представлен один из многочисленных вариантов общего случая последовательного соединения различных элементов.
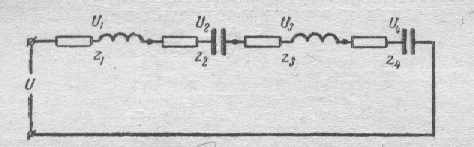
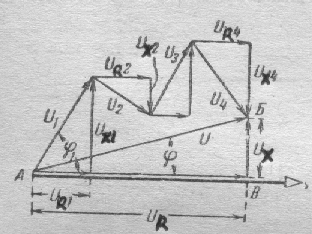
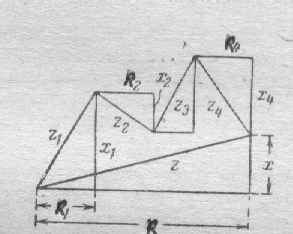
РИС.144 РИС.145 РИС.146
На рис.145 показано построение
векторной диаграммы напряжений для
данной цепи, которая позволяет рассчитать
амплитуду общего напряжения цепи и
сдвиг фаз между током и напряжением
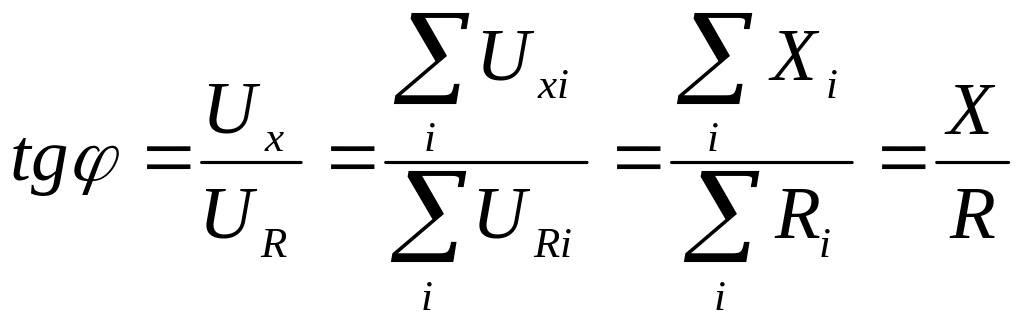 .
На рис. 146 представлено построение
общего треугольника сопротивлений,
который позволяет рассчитать общий
импеданс цепи и также сдвиг фаз между
током и напряжением:
.
На рис. 146 представлено построение
общего треугольника сопротивлений,
который позволяет рассчитать общий
импеданс цепи и также сдвиг фаз между
током и напряжением:
![]() .
.
Активное сопротивление всей цепи R является арифметической суммой активных сопротивлений на всех участках, а реактивное сопротивление всей цепи X – алгебраическая сумма всех реактивных сопротивлений.
