17.Числовые вероятностные характеристики случайных погрешностей

Вероятностной характеристикой случайных погрешностей как случайных величин является закон распределения вероятностей. Чтобы характеризовать случайные погрешности, пользуются числовыми вероятностными характеристиками случайных погрешностей, которые называют начальными и центральными моментами.

1)МО, дисперсии, СКО, коэф ассиметрии, эксцесс, мода, медиана и тд.

Моменты-это средние значения и называются начальными, если усредняются величины, отсчитываемые от начала координаты, и центральными – от центра функции плотности вероятности.

Начальные моменты порядка r результатов наблюдений представляют собой МО степени х^r

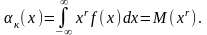
Первый начальный момент совпадает с МО результатов наблюдений, т.е.

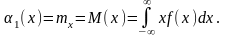
МО является оценкой истинного значения измеряемой величины.

Центральными(центриров.) моментами r-го порядка результатов наблюдений называют интеграл вида 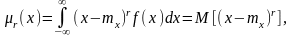который получают при смещении начала координат плотности распределения вероятностей в точку m_x. Первый центральный момент равен 0. Второй – это дисперсия результатов наблюдений:

Дисперсия – характеристика рассеяния результатов наблюдений относительно мат.ожидания. Дисперсия увеличивается с увеличением рассеяния результатов наблюдения. В качестве характеристики рассеяния используется СКО (положительное значение квадратного корня дисперсии):

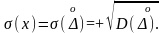
Третий центральный момент характеризует асимметрию распределения случайных погрешностей, т.е. скошенность. Коэффициент асимметрии:

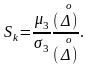
Четвертый центральный момент характеризует форму, плосковершинность или островершинность распределения случайных погрешностей и описывается с помощью эксцесса:

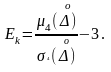
Число 3 вычитают потому, что для нормального распределения погрешностей

. Выражение 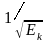называется контрэксцессом.

18.Законы распределения вероятностей случайных погрешностей

1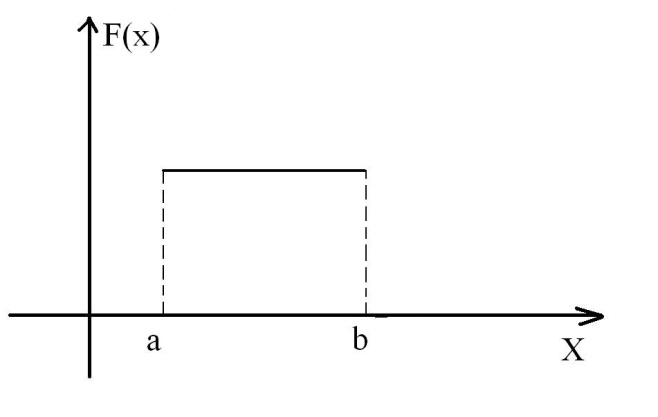 )Равномерный закон распределения. Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [a, b], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.е.

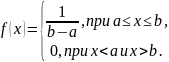
Обозначение: .

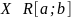Математическое ожидание: .

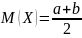Дисперсия: .

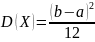Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, при статистическом моделировании наблюдений, подчиненных заданному распределению.

2)Нормальный закон распределения. Непрерывная случайная величина X имеет нормальный закон распределения с параметрами a и 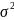, если ее плотность вероятности имеет вид:

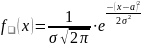
Обозначение: .

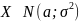Математическое ожидание: .

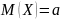Дисперсия: .

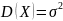Нормальный закон распределения с параметрами 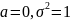, т.е. N(0;1), называется стандартным или нормированным.

Функция распределения нормально распределенной случайной величины имеет вид:

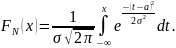
Нормальный закон распределения занимает центральное место в теории и практике вероятностно-статистических методов. Он является предельным законом, к которому приближаются многие другие законы распределения. Центральная предельная теорема теории вероятностей утверждает, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному.

3)Распределение Стьюдента (t-распределение). Пусть 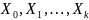– независимые стандартные нормальные случайные величины, такие что 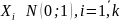. Тогда распределение случайной величины t:

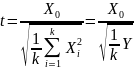
называется распределением Стьюдента с k степенями свободы, .

Обозначение: .

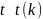Математическое ожидание: .

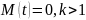Дисперсия: .

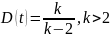Распределение Стьюдента сходится к стандартному нормальному при 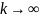. Распределение Стьюдента применяется в статистике для построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения.