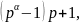- •Нод и нок нескольких целых чисел.
- •Конечные цепные дроби. Представление числа в виде конечной цепной дроби.
- •Подходящие дроби. Свойства подходящих дробей.
- •Систематические числа.
- •Простые числа. Свойства простых чисел.
- •Простые числа. Теорема Евклида о бесконечности множества простых чисел.
- •Простые числа. Решето Эратосфена.
- •Основная теорема арифметики.
- •Теорема о делимости натуральных чисел, разложенных на простые множители.
- •Кольцо целых гауссовых чисел . Норма целого гауссового числа и ее свойства. Пифагоровы числа.
- •Теорема о делении с остатком в кольце целых гауссовых чисел. Делители единицы (единицы) в кольце .
- •Делимость целых гауссовых чисел.
- •Линейные диофантовы уравнения. Представление всех решений линейного диофантова уравнения.
- •Количество и сумма натуральных делителей. Мультипликативные числовые функции.
- •Целая часть числа и ее свойства.
- •Сравнения и их свойства.
- •Полная система вычетов. Признак полной системы вычетов.
- •Приведенная система вычетов. Функция Эйлера. Признак приведенной системы вычетов.
- •Основная лемма о приведенных системах вычетов по двум взаимно простым модулям. Мультипликативность функции Эйлера.
- •Формула для вычисления функции Эйлера. Лемма Гаусса о сумме значений функции Эйлера по всем делителям данного числа.
- •Признак делимости Паскаля. Признак делимости на 2, 3, 4 и 5.
- •Признак делимости Паскаля. Признак делимости на 6, 7 и 8.
- •Признак делимости Паскаля. Признак делимости на 9 и 11.
- •Группа классов вычетов взаимно простых с модулем.
- •Теоремы Эйлера и Ферма.
- •Сравнения с одной неизвестной.
- •Линейные сравнения: критерий разрешимости и количество решений.
- •Периодические дроби. Теоремы о преобразовании несократимой дроби в периодическую дробь.
- •Правила преобразования периодической дроби в обыкновенную дробь.
- •Системы линейных сравнений. Система двух линейных сравнений и теорема о ее разрешимости. Китайская теорема об остатках.
- •Первообразные корни. Существование первообразных корней по простому модулю.
- •Индексы по простому модулю.
- •Теорема о свойствах индексов и следствие из нее.
- •Формула перехода от системы индексов с основанием к системе индексов с основанием (пример 1).
- •Двучленные сравнения. Решение двучленных сравнений. Квадратичные вычеты. Критерий Эйлера.
- •Теорема
- •Теорема
- •Критерий Эйлера
Формула для вычисления функции Эйлера. Лемма Гаусса о сумме значений функции Эйлера по всем делителям данного числа.
Эйлера по все м делителям данного числа.
Теорема.(Формула
для вычисления функции Эйлера): Пусть
 – каноническое разложение, тогда
– каноническое разложение, тогда .
Док-во: Пусть p
–
простое число и нужно вычислить
.
Док-во: Пусть p
–
простое число и нужно вычислить
 ,
для этого выпишем полну. Систему вычетов
по
,
для этого выпишем полну. Систему вычетов
по

1, |
2, |
… |
p, |
p+1, |
p+2, |
… |
2p, |
2p+1, |
2p+2 |
… |
3p, |
… |
… |
… |
… |
|
|
… |
|
В
каждом столбце, кроме последнего стоят
числа, взаимно простые с p,
а в последнем столбце стоят числа которые
делятся на p.
Всего
чисел в системе
 ,
а в последнем столбце
,
а в последнем столбце

Вывод:
чисел, взаимно простых с
,
будет
 это значит
это значит

Поскольку
функция Эйлера мультипликативна, то

Лемма
ГАУССА: Сумма
значений функции Эйлера по всем делителям
числа m
равна
m:
 – сумма по всем x,
которые
являются делителями m.
Доказательство: Пусть p
– простое число, рассмотрим сумму:
– сумма по всем x,
которые
являются делителями m.
Доказательство: Пусть p
– простое число, рассмотрим сумму:

 .
Пусть
.
Пусть
 –
каноническое разложение. Рассмотрим
выражение
–
каноническое разложение. Рассмотрим
выражение


Признак делимости Паскаля. Признак делимости на 2, 3, 4 и 5.
Общий
вид. Пусть натуральное число А записываемое
в десятичной системе счисления как
 ,
где
,
где
 - единицы,
- единицы,
 -
десятки и т.д.
-
десятки и т.д.
Пусть m – произвольное натуральное число, на которое мы хотим делить и выводить признак делимости на него. Находим ряд остатков по следующей схеме:
 -
остаток от деления 10 на m,
-
остаток от деления 10 на m,
 -
остаток от деления
-
остаток от деления
 на
m,
на
m,
 -
остаток от деления
-
остаток от деления
 на
m,
…,
на
m,
…,
 -
остаток от деления
-
остаток от деления
 на
m
на
m
Формально

Так
как остатков конечное число (а именно
m),
то этот процесс зациклится (не позже,
чем через m
шагов) и дальше можно его не продолжать.
Начиная с некоторого
 ,
где р – получившийся период
последовательности
,
где р – получившийся период
последовательности
 .
Для единообразия можно принять, что
.
Для единообразия можно принять, что
 .
Тогда А имеет тот же остаток от деления
на m,
что и число
.
Тогда А имеет тот же остаток от деления
на m,
что и число

Док-во. Пользуясь тем, что в алгебраическом выражении по модулю m можно заменять числа их остатками от деления на m, получаем

Признак делимости на 2
Здесь
m=2.
Так как
 ,
то
,
,
то
,
 .
Отсюда получаем известный признак:
остаток
от деления числа на 2 равен остатку от
деления его последней цифры на 2,
или обычно: число
делится на 2, если его последняя цифра
четна.
.
Отсюда получаем известный признак:
остаток
от деления числа на 2 равен остатку от
деления его последней цифры на 2,
или обычно: число
делится на 2, если его последняя цифра
четна.
Признак делимости на 3
Здесь
m=3.
Так как
 (остаток
от деления 10 на 3 равен 1), то все
(остаток
от деления 10 на 3 равен 1), то все
 .
Значит, остаток
от деления числа на 3 равен остатку от
деления суммы его цифр на 3,
или иначе: число
делится на 3, если сумма его цифр делится
на 3.
.
Значит, остаток
от деления числа на 3 равен остатку от
деления суммы его цифр на 3,
или иначе: число
делится на 3, если сумма его цифр делится
на 3.
Признак делимости на 4
Здесь
m=4.
Находим последовательность остатков:
 .
Отсюда получаем признак: остаток
от деления числа на 4 равен остатку от
деления
.
Отсюда получаем признак: остаток
от деления числа на 4 равен остатку от
деления
 на 4,
или, заметив, что остаток зависит только
от 2 последних цифр: число
делится на 4, если число, состоящее из 2
его последних цифр, делится на 4.
на 4,
или, заметив, что остаток зависит только
от 2 последних цифр: число
делится на 4, если число, состоящее из 2
его последних цифр, делится на 4.
Признак делимости на 5
Здесь
m=5.
Так как
 ,
то
,
то
 .
Отсюда получаем известный признак:
остаток
от деления числа на 5 равен остатку от
деления его последней цифры на 5,
или обычно: число
делится на 5, если его последняя цифра
– 0 или 5.
.
Отсюда получаем известный признак:
остаток
от деления числа на 5 равен остатку от
деления его последней цифры на 5,
или обычно: число
делится на 5, если его последняя цифра
– 0 или 5.