
- •Нод и нок нескольких целых чисел.
- •Конечные цепные дроби. Представление числа в виде конечной цепной дроби.
- •Подходящие дроби. Свойства подходящих дробей.
- •Систематические числа.
- •Простые числа. Свойства простых чисел.
- •Простые числа. Теорема Евклида о бесконечности множества простых чисел.
- •Простые числа. Решето Эратосфена.
- •Основная теорема арифметики.
- •Теорема о делимости натуральных чисел, разложенных на простые множители.
- •Кольцо целых гауссовых чисел . Норма целого гауссового числа и ее свойства. Пифагоровы числа.
- •Теорема о делении с остатком в кольце целых гауссовых чисел. Делители единицы (единицы) в кольце .
- •Делимость целых гауссовых чисел.
- •Линейные диофантовы уравнения. Представление всех решений линейного диофантова уравнения.
- •Количество и сумма натуральных делителей. Мультипликативные числовые функции.
- •Целая часть числа и ее свойства.
- •Сравнения и их свойства.
- •Полная система вычетов. Признак полной системы вычетов.
- •Приведенная система вычетов. Функция Эйлера. Признак приведенной системы вычетов.
- •Основная лемма о приведенных системах вычетов по двум взаимно простым модулям. Мультипликативность функции Эйлера.
- •Формула для вычисления функции Эйлера. Лемма Гаусса о сумме значений функции Эйлера по всем делителям данного числа.
- •Признак делимости Паскаля. Признак делимости на 2, 3, 4 и 5.
- •Признак делимости Паскаля. Признак делимости на 6, 7 и 8.
- •Признак делимости Паскаля. Признак делимости на 9 и 11.
- •Группа классов вычетов взаимно простых с модулем.
- •Теоремы Эйлера и Ферма.
- •Сравнения с одной неизвестной.
- •Линейные сравнения: критерий разрешимости и количество решений.
- •Периодические дроби. Теоремы о преобразовании несократимой дроби в периодическую дробь.
- •Правила преобразования периодической дроби в обыкновенную дробь.
- •Системы линейных сравнений. Система двух линейных сравнений и теорема о ее разрешимости. Китайская теорема об остатках.
- •Первообразные корни. Существование первообразных корней по простому модулю.
- •Индексы по простому модулю.
- •Теорема о свойствах индексов и следствие из нее.
- •Формула перехода от системы индексов с основанием к системе индексов с основанием (пример 1).
- •Двучленные сравнения. Решение двучленных сравнений. Квадратичные вычеты. Критерий Эйлера.
- •Теорема
- •Теорема
- •Критерий Эйлера
Периодические дроби. Теоремы о преобразовании несократимой дроби в периодическую дробь.


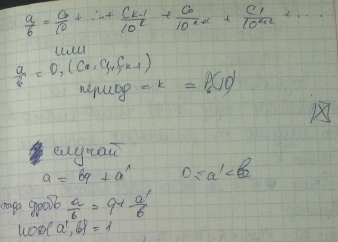

Правила преобразования периодической дроби в обыкновенную дробь.
Правило1: Чтобы записать число периодической дроби в виде обыкновенной дроби, надо период дроби записать в числителе, в знаменателе записать столько девяток, сколько цифр в периоде и полученную дробь добавить к целой части.
Правило2: Чтобы записать смешанную периодическую дробь в виде обыкновенной дроби, нужно от числа, которое стоит до второго периода, отнять число, которое стоит до первого периода и записать полученную разность в числитель. В знаменателе записать столько девяток, сколько цифр в периоде (S) и после девяток записать столько нулей, сколько цифр между запятой и первым периодом (t).
Системы линейных сравнений. Система двух линейных сравнений и теорема о ее разрешимости. Китайская теорема об остатках.
Рассмотрим
систему сравнений
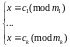 (1). Решить такую систему – значит найти
числа, удовлетворяющие каждому из этих
уравнений.
(1). Решить такую систему – значит найти
числа, удовлетворяющие каждому из этих
уравнений.
 Теорема.
Система (1) либо не имеет решений, либо
имеет одно решение, либо имеет одно
решение по модулю НОК [m1,
m2,
…, mk].
Док-во: ММИ по k:
k=2
Теорема.
Система (1) либо не имеет решений, либо
имеет одно решение, либо имеет одно
решение по модулю НОК [m1,
m2,
…, mk].
Док-во: ММИ по k:
k=2
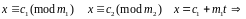
 . Если НОД (m1,
m2)=d
и (c2
–
c1)
не
. Если НОД (m1,
m2)=d
и (c2
–
c1)
не
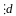 ,
то нет решений. Если (c2
–
c1
)
,
то нет решений. Если (c2
–
c1
)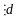 ,
то есть решение:
,
то есть решение:
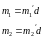 =>
=>
=>
=>
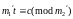 .
Получаем
.
Получаем
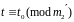 ,
значит
,
значит
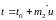 и
и
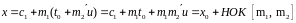 .
.
x0
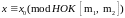 -
единственное решение. Пусть верно для
k
– 1 cравнений.
Докажем для k.
-
единственное решение. Пусть верно для
k
– 1 cравнений.
Докажем для k.
2 cлучай. 1) Система не имеет решений для случая k – 1 => вся система не имеет решений. 2) Система k – 1 сравнений имеет 1 решение.
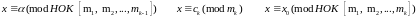
Следствие.
Система
(1) при попарно взаимно простых модулях
(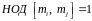 )
имеет ед. решение. Д-во: ММИ по k:
k=2
)
имеет ед. решение. Д-во: ММИ по k:
k=2
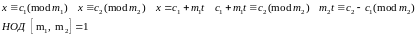
имеет единственное решение по модулю m1, m2.
Китайская теорема об остатках.
Если в системе сравнений модули попарно взаимно простые числа М=m1*m2*…*mk, a y – являются решениями таких сравнений:
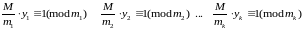 =>
=>
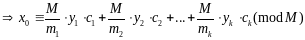 является
единственным решением по модулю М.
Док-во:
является
единственным решением по модулю М.
Док-во:
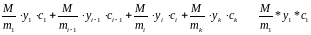
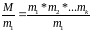 и
отсюда следует
и
отсюда следует
 .
.
Если
какое-то из сравнений сис-мы
 (2)
не имеет решение, то система не имеет
решений.
(2)
не имеет решение, то система не имеет
решений.
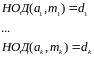 =>
Если сущ.
=>
Если сущ.
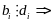 решений нет.
решений нет.
Если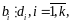 то
то
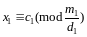
…
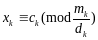
Первообразные корни. Существование первообразных корней по простому модулю.
Пусть НОД(a,m)=1.
Опр.
Класс
а
наз.
первообразным по модулю m,
если его порядок по модулю m
равен
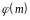 .
Т.е. P(a)=
.
.
Т.е. P(a)=
.
Теорема.
По
простому модулю m=p
существует
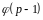 первообразных корней. Док-во: Класс
ар–1
=класс
1 – первообразный корень по
модулю
р. Поскольку, если р – простое и (р-1)
кратно k,
то
первообразных корней. Док-во: Класс
ар–1
=класс
1 – первообразный корень по
модулю
р. Поскольку, если р – простое и (р-1)
кратно k,
то
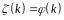 .
А это значит, что при k=р-1
получим
.
А это значит, что при k=р-1
получим
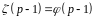 .
.
Теорема
Если
а первообразный корень по модулю m,
то числа а, а2,
… ,
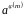 образуют
приведённую систему вычетов по модулю
m.
образуют
приведённую систему вычетов по модулю
m.
Теорема
Если
р-простое число, то
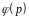 =р-1=р1α1р2а2…psas.
а является первообразным корнем по
модулю m
тогда и только тогда, когда
=р-1=р1α1р2а2…psas.
а является первообразным корнем по
модулю m
тогда и только тогда, когда
а в
степени
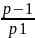 не сравнимо с 1 (mod
p)
не сравнимо с 1 (mod
p)
…
а в
степени
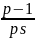 не сравнимо с 1 (mod
p).
не сравнимо с 1 (mod
p).
Док-во:
Необходимость очевидна(если хотя бы одно сравнение имело бы место, то а не было бы первообразным корнем).
Достаточность.
Пусть выполняются все соотношения.
Докажем, что а первообразный корень.
Если для любого k
(р–1) кратно k,
тогда k
делит одно из этих чисел
, … ,
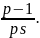 тогда
найдётся такое i,
что
тогда
найдётся такое i,
что
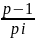 кратно
k.
Значит,
=kl,
l
– натуральное. А это значит, а в степени
=akl=(ak)l
сравнимо
1(mod
p).
Значит, а в степени
сравнимо
1(mod
p),
что невозможно в силу условия.
кратно
k.
Значит,
=kl,
l
– натуральное. А это значит, а в степени
=akl=(ak)l
сравнимо
1(mod
p).
Значит, а в степени
сравнимо
1(mod
p),
что невозможно в силу условия.
