7. Простые числа. Решето Эратосфена.

Опр1. Натурал. число 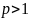наз. простым, если оно делится только на 1 и себя (др. натур. Делителей нет; др. полож. целых делителей не имеет).

Опр2. Натур. число наз. составным, если оно имеет делители кроме 1 и себя. 1 не является ни простым, ни составным числом.

Решето Эратосфена. Нахождение простых чисел, меньших данного натурального числа n.

Св-во 1: если натур. число не делится ни на одно простое число 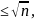то оно простое. (другими словами: любое составное число делится на простое число, не превосходящее 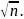Или если n явл. Составным числом, то 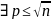, (p- простое число, такое что n .

Эквивалентное утверждение: если nєN не делится ни на одно p (p- простое число, p≤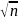 , p>1. n- простое число. Док-во: Пусть p₁- наименьший простой делитель n, тогда n=p₁n₁ (n₁>1) и p₁<n₁. Пусть p₁>n₁, тогда любое простое число, которое делит n₁, делит n, и оно будет меньше p₁- противоречие. n=p1n1≥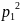 →p1≤ . Ч.т.д.

Св-во 2: если в мн-ве натуральных чисел {2,3,…} вычеркнуть числа, кратные первым s простым числам p₁=2, p₂=3, p₃=5,…, p_s, то первое следующие за p_s незачёркнутое число (p_s+1) явл. простым. Док-во: (от противного) если бы оно было составным, то делилось по крайней мере на одно простое число ≤ p_s. Но все числа кратные простым числам ≤ p_s уже вычеркнуты – противоречие. Ч.т.д.

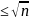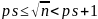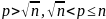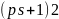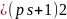Св-во 3: Если на мн-ве натуральных чисел {2,3,…,n,…} вычеркнуть все числа, кратные всем простым числам (выбрать s так, чтобы ) то оставшиеся числа будут совпадать с множеством простых чисел . Док-во: простым явл. незачёркнутое число, меньше , т.к. составные числа имеют простой делитель 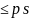и уже ранее вычеркнутый. Ч.т.д.

Алгоритм: на мн-ве натуральных чисел {2,3,…,n,..} первое число 2 – простое. Вычёркиваем все числа, кратные 2. Тогда первое следующее за 2 невычеркнутое число 3 – простое; вычёркиваем все числа, кратные 3. Первое невычеркнутое число 5 – простое. Вычёркиваем все числа, кратные 5….Продолжаем этот процесс, пока не вычеркнем все числа, кратные найденным простым числам 2,3, …,p_s где

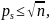а следующее простое 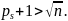Все оставшиеся невычеркнутые числа дадут нам мн-во простых чисел, между и n. И вместе с найденными ранее простыми числами. Т.обр. получаем все простые числа, не превосходящие n.

2 3 4 5 6 7 8 9 10

11 12 13 14 15 16 17 18 19 20 …

8. Основная теорема арифметики.

Т. Каждое натуральное число >1 раскладывается в произведение простых чисел. Такое разложение единственное с точностью до порядка следования сомножителей. Док-во: 1. Существование. ММИ по n. 1) n=2, 2=2. 2) допустим, что произвольное натуральное число < n раскладывается на простые множители. 3) докажем, что n раскладывается на простые множители. По св-ву (каждое натур. число n>1 имеет хотя бы 1 простой делитель) n имеет хотя бы 1 простой делитель p₁ и тогда мы n можем записать n=p₁n₁, n₁<n. Возможны 2 случая: 1) n₁=1, n=p₁. 2) n₁>1, то по предположению следующие n₁=p₂p₃…p_k – произведение простых чисел, тогда наши n в этом случае равно n=p₁p₂p₃…p_k 2. Единственность ММИ по n. 1)n=2; 2) пусть единственность имеет место для любого натурального числа <n. 3) докажем для n (от противного). Пусть n с одной стороны n=p₁p₂….p_n. Или n=q₁q₂…q_s… Тогда p₁p₂…p_k=q₁q₂…q_s . Левая часть рав-ва делится на p₁, значит, и правая часть делится на p₁. Следовательно, одни из сомножителей q₁,q₂,…,q_s совпадает с p₁. Без ограничения общности можем считать, что p₁=q₁. Раз p₁=q₁, сократим на p₁. Получим p₂…p_k=q₂….q_s. (p2…pk)<n, поэтому по предположению индукции такое представление единственное. Значит k=s и простые числа q₂…q_s отличаются от простых чисел только порядком следования. Ч.т.д.

Опр. Представление натурального числа n в виде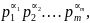 n= где p₁,p₂,…,p_m – простые числа, α_i- натуральные числа, назыв. каноническим представлением (каноническим разложением) числа n.

Опр. Каноническим разложением целого числа а (а≠0, а≠±1) на простые множители наз. представление числа а в виде a=± где p₁…p_m – разные простые числа, α_i- натуральные числа.