18. Приведенная система вычетов. Функция Эйлера. Признак приведенной системы вычетов.

Лемма: .

Комментарий: если числа сравнимы по mod m, то они имеют с модулем один и тот же общий делитель.

Замечание: если , .т.е. если одно число из класса вычетов взаимнопростое с модулем, то любое другое число из этого же класса взаимнопростое с модулем.

Замечание: привед.сис.выч. можно получить след.образом: взять из каждого класса вычетов взаимнопростого с модуля m по одному представителю.

Опр. Привед.сис.вычетов по mod m – это набор чисел из полной сис.вычетов (рассматриваем систему наим.неотр.вычетов).

Пример: Полная система вычетов по mod 6: 0,1,2,3,4,5. Приведенная система вычетов по mod 6: 1,5.

Опред. Функцией Эйлера наз.функция , такая, что количество натур.чисел не больших m и взаимно простых с m.

m	1	2	3	4	5	6	7	8
	1	2	2	2	4	2	6	4

Замечание: Если p- простое число, то .

Замечание: Количество чисел в приведенной системе вычетов=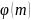

Теорема(признак): Система , попарно не сравнимых по mod m и взаимно простых с mod m целых чисел образуют прив.сис.вычетов по mod m. Док-во: пусть a₁,a₂,…,a -система чисел описанная в теореме. 1) 2)НОД ( )=1, . 1)=> в разных классах.2) принадлежат разным классам вычетов взаимно простых с модулем. Количество чисел представители которых взаимно просты с m совпадают , поэтому в каждом классе попался только одно из этих чисел

Правило: чтобы выяснить явл.ли система чисел { } приведенной системой вычетов по mod m нужно взять остатки от деления x_i по :если получаем (без повторов) и они взаимно просты с m то система будет приведенной по mod m.

Пример: 9,2,16,20,27,39,46,85. Решение: 1) явл.ли эта система вычетов по mod 8.2) приведенной системой вычетов по mod 8 1)1,2,0,4,3,7,6,5, – полная система вычетов 2) не является приведенной т.к. не все остатки взаимно просты с 8. Приведенная система вычетов:1,3,7,5 9,27,39,85

19. Основная лемма о приведенных системах вычетов по двум взаимно простым модулям. Мультипликативность функции Эйлера.

Основная ЛЕММА. Пусть a,b – взаимно простые числа; – приведенная система вычетов по mod(a) и – приведенная система вычетов по mod(b), тогда множество

– приведенная система вычетов по mod(ab). Доказательство. Что нужно доказать: 1) Каждое число взаимно просто с mod(ab). 2) Каждое число x, взаимно простое с mod(ab), сравнимо с некоторым по mod(ab) . 3) Разные числа попарно не сравнимые.

1. Докажем что НОД( ,а)=1. Допустим что

но НОД(b,a)=1 и , значит НОД( ,а)=1.

2. Число x взаимно просто с ab, значит x взаимно просто а, с другой стороны – приведенная система вычетов по mod(a), поэтому , аналогично

значит

.

3.

аналогично i=s

Теорема. Функция Эйлера мультипликативна – это значит если a,b – взаимно просты, то . Доказательство: Рассмотрим множество из леммы – количество чисел в нем равно , так как множество М это приведенная система вычетов по . С другой стороны, так как , то разных комбинаций (a,b) может быть