
- •Нод и нок нескольких целых чисел.
- •Конечные цепные дроби. Представление числа в виде конечной цепной дроби.
- •Подходящие дроби. Свойства подходящих дробей.
- •Систематические числа.
- •Простые числа. Свойства простых чисел.
- •Простые числа. Теорема Евклида о бесконечности множества простых чисел.
- •Простые числа. Решето Эратосфена.
- •Основная теорема арифметики.
- •Теорема о делимости натуральных чисел, разложенных на простые множители.
- •Кольцо целых гауссовых чисел . Норма целого гауссового числа и ее свойства. Пифагоровы числа.
- •Теорема о делении с остатком в кольце целых гауссовых чисел. Делители единицы (единицы) в кольце .
- •Делимость целых гауссовых чисел.
- •Линейные диофантовы уравнения. Представление всех решений линейного диофантова уравнения.
- •Количество и сумма натуральных делителей. Мультипликативные числовые функции.
- •Целая часть числа и ее свойства.
- •Сравнения и их свойства.
- •Полная система вычетов. Признак полной системы вычетов.
- •Приведенная система вычетов. Функция Эйлера. Признак приведенной системы вычетов.
- •Основная лемма о приведенных системах вычетов по двум взаимно простым модулям. Мультипликативность функции Эйлера.
- •Формула для вычисления функции Эйлера. Лемма Гаусса о сумме значений функции Эйлера по всем делителям данного числа.
- •Признак делимости Паскаля. Признак делимости на 2, 3, 4 и 5.
- •Признак делимости Паскаля. Признак делимости на 6, 7 и 8.
- •Признак делимости Паскаля. Признак делимости на 9 и 11.
- •Группа классов вычетов взаимно простых с модулем.
- •Теоремы Эйлера и Ферма.
- •Сравнения с одной неизвестной.
- •Линейные сравнения: критерий разрешимости и количество решений.
- •Периодические дроби. Теоремы о преобразовании несократимой дроби в периодическую дробь.
- •Правила преобразования периодической дроби в обыкновенную дробь.
- •Системы линейных сравнений. Система двух линейных сравнений и теорема о ее разрешимости. Китайская теорема об остатках.
- •Первообразные корни. Существование первообразных корней по простому модулю.
- •Индексы по простому модулю.
- •Теорема о свойствах индексов и следствие из нее.
- •Формула перехода от системы индексов с основанием к системе индексов с основанием (пример 1).
- •Двучленные сравнения. Решение двучленных сравнений. Квадратичные вычеты. Критерий Эйлера.
- •Теорема
- •Теорема
- •Критерий Эйлера
Линейные диофантовы уравнения. Представление всех решений линейного диофантова уравнения.
Линейным диофантовым уравнением наз. уравнение вида b=a1x1+a2x2+...+anxn (1), где все коэффициенты и свободный член – целые гауссовы числа.
Решение
ищется в целых числах. Решением такого
уравнения наз. упорядоченная совокупность
чисел (к1,к2,...,кn),ki
 Z,
n
N,
которое данное уравнение превращает в
тождество a1k1+...+ankn=b
(2)
Z,
n
N,
которое данное уравнение превращает в
тождество a1k1+...+ankn=b
(2)
Критерий разрешимости: уравнение (1) разрешимо <=> НОД коэффициентов уравнения делит свободный член: b НОД(a1,...,an)=d (3). Док-во: пусть к1,к2,...,кn- решение, а раз решение, то подставляя в уравнение (1) и получаем (2).
a1 d,..., an d => (a1k1+...+ankn ) d <= дано: b d, b=db1 д-ть, что есть решение
д-во: a1с1+...+anсn=b, сi Z an d =>(a1k1+...+ankn ) d =>b d
Общее
решение диофантового уравнения:

Общий
метод решения: 1) ai= 1
,
Xi=
b-a1x1+a2x2+...+anxn
, x1,…,xn
-
свободные неизвестные , ( k1,…,kn
)-
решения 2) ai
1
,
Xi=
b-a1x1+a2x2+...+anxn
, x1,…,xn
-
свободные неизвестные , ( k1,…,kn
)-
решения 2) ai 1,
1,
 =1
– наименьшее
=1
– наименьшее
Каждый
коэффициент разделим на a1
ai=a1qi+r1,
o ri
ri
a1x1+( a1q2+r2)x2+…+( a1qn+rn)xn=b
a1x1+ a1q2 x2+ r2x2+…+ a1qnxn+rnxn=b
a1(x1+ q2 x2+ …+ qnxn) + r2x2+…+rnxn=b
x1+ q2 x2+ …+ qnxn=y1 a1y1 + r2x2+…+rnxn=0 (*)
док-во: пусть a1k1+...+ankn=b- верное равенство. Тогда (к1,к2,...,кn)-решение уравнения. k1+ q2 k2+ …+ qnkn=y1 подставим в (*): a1(k1+ q2 k2+ …+ qnkn) + +r2k2+…+rnkn= a1k1+( a1q2+r2)k2+…+ (a1qn+rn)kn=a1k1+a2k2+…+ankn=b
2) обратимо: (любое решение (*) дает решение уравнения)
Пусть (m1,m2,...,mn)-решение уравнения (*). Получаем a1m1+a2m2+…+anmn=b
X1+q2m2+…+qnmn=m1, X1= m1– q2m2–…–qnmn
(m1– q2m2–…–qnmn, m2,…,mn) – решение
a1(m1– q2m2–…–qnmn)+a2m2+…+anmn=a1m1– a1 q2m2–…–a1
qnmn+a2m2+…+anmn= a1m1+( a1 q2+r2–a1 q2)m2+…+(a1 qn+rn– a1qn)mn= =a1m1+r2m2+…+rnmn=b
Количество и сумма натуральных делителей. Мультипликативные числовые функции.
Опр.
Пусть
n N,число
натуральных делителей числа n
будем обозначать
N,число
натуральных делителей числа n
будем обозначать
 ,сумму
натуральных делителей
,сумму
натуральных делителей

Теорема1.
Пусть натуральное число n>1 имеет
представление
n=
 …..
….. тогда
тогда
=

1)Каждый натуральный делитель числа n может быть записан в виде
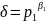
 …..
….. где 0
где 0 .Чтобы найти количество делителей нужно
посчитать количество всех возможных
комбинаций s-упорядочных показателей
степеней (
.Чтобы найти количество делителей нужно
посчитать количество всех возможных
комбинаций s-упорядочных показателей
степеней ( 0
0

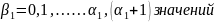
 ……….
……….
Так
как

Всего
значений

2)рассмотрим произведения
(1+ +…..+
)
+…..+
)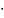 (1+
(1+ +…..+
+…..+ )…(1+
)…(1+ +…..+
)
+…..+
)
 0
0

Опр.Числовая
функция f: наз. мультипликативной, если НОД(m,n)=1
наз. мультипликативной, если НОД(m,n)=1
f(m
Теорема2.
Ф-ии

НОД(m,n)=1
m=
…..
n=
 …..
….. ,
,

тогда
 …..
….. …..
)=
…..
)=
=( )(
)( )=
)=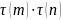
аналогично
и для

Целая часть числа и ее свойства.
[x] – эта ф-я задается на множ-ве R. Каждому действит числу ставится в соотв целое наибольшее число, не превыш. данное.
Пример:
[3,2]=3, [-5,1]=-6, {x}=x-[x] n [x]<n+1,
0
{x}<1
[x]<n+1,
0
{x}<1
Дробная часть{-5,1}=0,9
Теорема
1: Пусть

 R,
d
R,
d N.
Тогда число положит чисел, не превосходящих
N.
Тогда число положит чисел, не превосходящих
 равно
равно
 .
.
Док-во:
рассм. числа, кратные d.
d,2d,…,sd,
где sd
 <(s+1)d,
s=
<(s+1)d,
s= .
Ч.т.д.
.
Ч.т.д.
Теорема 2:
Пусть
р – простое нат число, n
N,
n 1,
показатель, с кот данное простое р входит
в каноническое разложение n!
равно
1,
показатель, с кот данное простое р входит
в каноническое разложение n!
равно

Пример. С каким показателем число 3 входит в 40!

