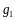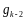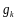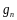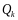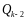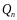- •Нод и нок нескольких целых чисел.
- •Конечные цепные дроби. Представление числа в виде конечной цепной дроби.
- •Подходящие дроби. Свойства подходящих дробей.
- •Систематические числа.
- •Простые числа. Свойства простых чисел.
- •Простые числа. Теорема Евклида о бесконечности множества простых чисел.
- •Простые числа. Решето Эратосфена.
- •Основная теорема арифметики.
- •Теорема о делимости натуральных чисел, разложенных на простые множители.
- •Кольцо целых гауссовых чисел . Норма целого гауссового числа и ее свойства. Пифагоровы числа.
- •Теорема о делении с остатком в кольце целых гауссовых чисел. Делители единицы (единицы) в кольце .
- •Делимость целых гауссовых чисел.
- •Линейные диофантовы уравнения. Представление всех решений линейного диофантова уравнения.
- •Количество и сумма натуральных делителей. Мультипликативные числовые функции.
- •Целая часть числа и ее свойства.
- •Сравнения и их свойства.
- •Полная система вычетов. Признак полной системы вычетов.
- •Приведенная система вычетов. Функция Эйлера. Признак приведенной системы вычетов.
- •Основная лемма о приведенных системах вычетов по двум взаимно простым модулям. Мультипликативность функции Эйлера.
- •Формула для вычисления функции Эйлера. Лемма Гаусса о сумме значений функции Эйлера по всем делителям данного числа.
- •Признак делимости Паскаля. Признак делимости на 2, 3, 4 и 5.
- •Признак делимости Паскаля. Признак делимости на 6, 7 и 8.
- •Признак делимости Паскаля. Признак делимости на 9 и 11.
- •Группа классов вычетов взаимно простых с модулем.
- •Теоремы Эйлера и Ферма.
- •Сравнения с одной неизвестной.
- •Линейные сравнения: критерий разрешимости и количество решений.
- •Периодические дроби. Теоремы о преобразовании несократимой дроби в периодическую дробь.
- •Правила преобразования периодической дроби в обыкновенную дробь.
- •Системы линейных сравнений. Система двух линейных сравнений и теорема о ее разрешимости. Китайская теорема об остатках.
- •Первообразные корни. Существование первообразных корней по простому модулю.
- •Индексы по простому модулю.
- •Теорема о свойствах индексов и следствие из нее.
- •Формула перехода от системы индексов с основанием к системе индексов с основанием (пример 1).
- •Двучленные сравнения. Решение двучленных сравнений. Квадратичные вычеты. Критерий Эйлера.
- •Теорема
- •Теорема
- •Критерий Эйлера
Конечные цепные дроби. Представление числа в виде конечной цепной дроби.
Опр.:
Конечной цепной дробью наз. число,
записанное в виде
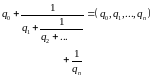 ,
где
,
где
 – целое число,
– целое число,
 .
Элементы
.
Элементы
 наз. элементами цепной дроби.
наз. элементами цепной дроби.
Примеры: Можем ли мы целое число представить в виде конечной цепной дроби? Ответ: Да 3=(3).
Если
не поставить условие
 ,
то одно и то же рациональное число можно
представить двумя способами в виде
цепной дроби.
,
то одно и то же рациональное число можно
представить двумя способами в виде
цепной дроби.
ВЫДЕЛЕНИЕ ЦЕЛОЙ ЧАСТИ:
Пусть
 ,
тогда существует единственное
представление
,
тогда существует единственное
представление

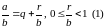 .
.
Примеры:
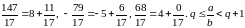 .
.
Опр.:
Целой частью рационального числа
 наз. наибольшее целое число, не
превосходящее рациональное число
.
Обозначение:
наз. наибольшее целое число, не
превосходящее рациональное число
.
Обозначение:
 .
.
Опр.:
Дробной частью числа
наз. разность
 .
Обозначение:
.
Обозначение:
 .
.
Примеры:

Опр.:
Определение целой части
 согласно формулам (1), наз. выделением
целой части.
согласно формулам (1), наз. выделением
целой части.
 .
.
РАЗЛОЖЕНИЕ РАЦИОНАЛЬНОГО ЧИСЛА В ВИДЕ КОНЕЧНОЙ ЦЕПНО ДРОБИ:
Пусть
 .
Применим к
.
Применим к
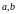 алгоритм Евклида для нахождения НОД.
алгоритм Евклида для нахождения НОД.


 .
.
Т.: Любое рациональное число можно представить в виде конечной цепной дроби.
Пример:
Разложить рациональное число в конечную
цепную дробь.
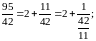
 Запишем теперь цепную дробь:
Запишем теперь цепную дробь:
 .
.
Т.:
Представление рационального числа в
виде конечной цепной дроби однозначно
(конечно).
Целая часть цепной дроби равна ее первому
элементу
 .
Число элементов дроби >2 – аналогично.
.
Число элементов дроби >2 – аналогично.
Предположим

 Повторным сравнением целых частей
получаем
Повторным сравнением целых частей
получаем
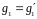 .
.
 Если
Если
 .
Если
.
Если
 - противоречие.
- противоречие.
Подходящие дроби. Свойства подходящих дробей.
Опр.:
Дроби вида
 называют подходящими дробями.
называют подходящими дробями.
 - подходящая дробь порядка
- подходящая дробь порядка


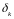 переходит
в
переходит
в
 ,
если в
заменить выражением
:
,
если в
заменить выражением
:

 На
основании ММИ получаем:
На
основании ММИ получаем:
 - рекуррентные формулы для вычислений
подходящих дробей, а также их числителей
и знаменателей.
- рекуррентные формулы для вычислений
подходящих дробей, а также их числителей
и знаменателей.
 Схема
для вычисления подходящих дробей:
Схема
для вычисления подходящих дробей:

|
|
|
|
|
… |
|
|
|
… |
|
|
1 |
|
|
|
… |
|
|
|
… |
|
|
0 |
|
|
|
… |
|
|
|
… |
|
Свойства
подходящих дробей:
 .
По формуле (*)
.
По формуле (*)
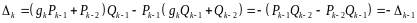 т.е.
все
т.е.
все
 по абсолютной величине все равны.
по абсолютной величине все равны.

 .
.
Следствие:
 .
.
Следствие:
Все подходящие дроби
 являются несократимыми. Если
являются несократимыми. Если
 - несократимая дробь, а
- несократимая дробь, а
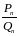 - ее последняя походящая дробь, то
- ее последняя походящая дробь, то

Следствие:
 .
.


Следствие:
Пусть
 предпоследняя подходящая дробь для
данного разложения
предпоследняя подходящая дробь для
данного разложения
 в циклическую дробь. Тогда
в циклическую дробь. Тогда
 .
.
Систематические числа.
Определения:
основанием позиционной системы счисления называется некоторое определенное натуральное число
 ;
;число 0, 1, 2, …,
 называются цифрами;
называются цифрами;натуральное число
 представленное в виде:
представленное в виде:
 ,
где
,
где
 - цифры и
- цифры и
 называется
называется
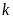 -значным
систематическим числом с основанием
-значным
систематическим числом с основанием
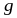 ;
;место занимаемое цифрой при написании числа позиционной системе называется разрядом;
в зависимости от выбора основания
 систематическое число называется
двоичным при
систематическое число называется
двоичным при
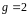 ,
троичным при
,
троичным при
 ,
десятичным при
,
десятичным при
 и т.д.;
и т.д.;
обозначение
 .
.
Теорема:
каждое натуральное число можно однозначно
записать в виде систематического числа
системы счисления с основанием
 .
.
Операции
над систематическими числами проводятся
по тем же правилам, что и в десятичной
системе счисления. Каждый раз когда
получается число
 основанию системы счисления нужно
сделать перенос в следующий разряд.
основанию системы счисления нужно
сделать перенос в следующий разряд.