27. Линейные сравнения: критерий разрешимости и количество решений.

Теорема. Пусть НОД(a,m) = d. Сравнение ax≡b(mod m) имеет решение т.и.т когда d делит b. Если b:d, то сравнение имеет d решений.

Цепные дроби =a₁ +

× =

P_n×Q_n-1-Q_nP_n-1=(-1)ⁿ

m×Q_n-1 - a× P_n-1=(-1)ⁿ

–a× P_n-1≡(–1)ⁿ (mod m)

a× P_n-1≡(–1)^n-1 (mod m) или (–1)^n-1 a× P_n-1 ≡1 (mod m)

(–1)^n-1 a× P_n-1 ≡b (mod m)

получаем

x≡(–1)^n-1 b× P_n-1 (mod m) – решение сравнения первой степени с одним неизвестным.

Пример:

111x≡75(mod 321) |:3|

37x≡25(mod 107)

d = 3 => три решения

= 2 + =2 + = 2 +

= 1 + = 1+ = 8 + = 8 +

n=4

		2	1	8	4
qs
ps	1	2	3	26	107

28. Метод подбора решения линейных сравнений.

1)5x 7(mod 8)

НОД(5,8)=1 => 1- решение

Проверим числа с помощью системы вычетов по mod 8

0; ±1; ±2; ±3; 4;

x≡3(mod 8)

2) 6x≡7(mod 15)

НОД(6,15)=3, но 7 не кратно 3 => сравнение не имеет решений

3) 15x≡35(mod 55)

3x≡7(mod 11)

x≡6(mod 11); x≡6(mod 55); x≡17(mod 55)

x≡39(mod 55); x≡50(mod 55);

29. Решение линейных сравнений с помощью теоремы Эйлера.

λ≡a^ɸ(m)–1b(mod m)

1)9x≡8(mod 34)

x≡a^ɸ(m)–1b(mod m), НОД(9, 34)=1 – значит сравнение имеет единственное решение

ɸ(34)=ɸ(2×17)=1×16=16

x≡9¹⁶×8(mod 34) |:| x≡3³⁰×8(mod 34)

x≡3¹⁴×8(mod 34)

x≡3^–2×8(mod 34)

x≡23²×8(mod 34)≡529×8(mod 34)

30. Решение линейных сравнений методом преобразования коэффициентов.

1) 5x≡7(mod 8)

5x≡15(mod 8) => x≡3(mod 8)

2)7x≡6(mod 15)

7x≡21(mod 15) => x≡3(mod 15)

3)17x≡25(mod 28)

45x≡25(mod 28)

9x≡5(mod 28) => 9x≡5–140(mod 28) =>

9x≡–135(mod 28)

x≡–15(mod 28) => x≡13(mod 28)

31. Порядок числа по данному модулю.

Теорема. (НОД(a,m)=1). Если , то P(a)=P(b). Док-во. , по определению , а значит 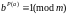, P(a) P(b). , Если числа сравнимы по модулю, то их порядки одинаковы. ч.т.д.

Следствие. Все числа одного и того же класса имеют одни и те же порядки.

Теорема. Если Док-во:

Cледствие. Порядок элемента делит , т.е. . Это следует из теоремы Эйлера.

Теорема. a^s a^t когда . Д-во: НЕОБХОДИМОСТЬ:

a^s a^t s и t – натуральные, . Разделим => 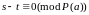, . Достаточность: , тогда , k Z. => .

Теорема. Все числа последовательности а, а², … , а^k, … (1), все а^k P(a) классам, и вычетами которой в каждом классе будет а, а², … , а^P(a) (2). Док-во: Все числа последов-сти (2) попарно несравнимы по модулю m, .

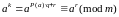Теорема. Порядок элемента P(a^s)=P(a)  НОД (s, P(a))=1. Док-во: пусть НОД (s, P(a))=1. Рассмотрим у – такая степень элемента, что a^s , => (a^s)^y , => , но по условию НОД (s, P(a))=1 и . Если же НОД (s, P(a))=d > 1, то порядок а^s не совпадает с порядком P(a), покажем это 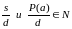. Рассмотрим .

Теорема. Обозначим порядок P(a)=k. Тогда классы представляют различные решения сравнения , эти все классы различны. Док-во: Если .

Пример. m=36, P(5)=6, тогда .

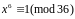Решение. .

Замечание. Если m=p – простое число, то других решений НЕТ, оно имеет не больше чем k решений.