
- •Нод и нок нескольких целых чисел.
- •Конечные цепные дроби. Представление числа в виде конечной цепной дроби.
- •Подходящие дроби. Свойства подходящих дробей.
- •Систематические числа.
- •Простые числа. Свойства простых чисел.
- •Простые числа. Теорема Евклида о бесконечности множества простых чисел.
- •Простые числа. Решето Эратосфена.
- •Основная теорема арифметики.
- •Теорема о делимости натуральных чисел, разложенных на простые множители.
- •Кольцо целых гауссовых чисел . Норма целого гауссового числа и ее свойства. Пифагоровы числа.
- •Теорема о делении с остатком в кольце целых гауссовых чисел. Делители единицы (единицы) в кольце .
- •Делимость целых гауссовых чисел.
- •Линейные диофантовы уравнения. Представление всех решений линейного диофантова уравнения.
- •Количество и сумма натуральных делителей. Мультипликативные числовые функции.
- •Целая часть числа и ее свойства.
- •Сравнения и их свойства.
- •Полная система вычетов. Признак полной системы вычетов.
- •Приведенная система вычетов. Функция Эйлера. Признак приведенной системы вычетов.
- •Основная лемма о приведенных системах вычетов по двум взаимно простым модулям. Мультипликативность функции Эйлера.
- •Формула для вычисления функции Эйлера. Лемма Гаусса о сумме значений функции Эйлера по всем делителям данного числа.
- •Признак делимости Паскаля. Признак делимости на 2, 3, 4 и 5.
- •Признак делимости Паскаля. Признак делимости на 6, 7 и 8.
- •Признак делимости Паскаля. Признак делимости на 9 и 11.
- •Группа классов вычетов взаимно простых с модулем.
- •Теоремы Эйлера и Ферма.
- •Сравнения с одной неизвестной.
- •Линейные сравнения: критерий разрешимости и количество решений.
- •Периодические дроби. Теоремы о преобразовании несократимой дроби в периодическую дробь.
- •Правила преобразования периодической дроби в обыкновенную дробь.
- •Системы линейных сравнений. Система двух линейных сравнений и теорема о ее разрешимости. Китайская теорема об остатках.
- •Первообразные корни. Существование первообразных корней по простому модулю.
- •Индексы по простому модулю.
- •Теорема о свойствах индексов и следствие из нее.
- •Формула перехода от системы индексов с основанием к системе индексов с основанием (пример 1).
- •Двучленные сравнения. Решение двучленных сравнений. Квадратичные вычеты. Критерий Эйлера.
- •Теорема
- •Теорема
- •Критерий Эйлера
Нод и нок нескольких целых чисел.
Опр.:
Пусть
 .
Целое число
.
Целое число
 называется общим делителем
называется общим делителем
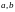 ,
если
,
если

Опр.:
Пусть
,
хотя бы одно из которых не равно нулю.
Наибольшим общим делителем
называется целое число
 ,
которое является общим делителем
и кратно любому их общему делителю.
,
которое является общим делителем
и кратно любому их общему делителю.

Лемма1:
Если существует
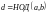 ,
то
,
то
 .
.
 ,
,
 .
Пусть
.
Пусть
 - общий делитель
.
Тогда
- общий делитель
.
Тогда

Лемма2:
Если
 и
и
 ,
то
,
то
 .
.
 общий
делитель
общий
делитель
 ,
но аналогично получаем
,
но аналогично получаем
 ,
тогда
,
тогда
Лемма3:
Если
 (не обязательно деление с остатком), то
1)
(не обязательно деление с остатком), то
1)
 2)
2)
 .
Докажем сразу свойство 2, т.е. свойство
1 – частный случай свойства 2.
.
Докажем сразу свойство 2, т.е. свойство
1 – частный случай свойства 2.
 тогда
тогда
 . Пусть
. Пусть

Алгоритм Евклида
Пусть
 ,
тогда
,
тогда

 остаток равен нулю. Остатки от делений
– это целые неотрицательные числа,
которые удовлетворяют условию:
остаток равен нулю. Остатки от делений
– это целые неотрицательные числа,
которые удовлетворяют условию:
 .
Эта последовательность не может быть
бесконечной. Значит, на каком-то шаге
деления получится остаток =0. Этим и
объясняется последнее равенство (1).
Равенство (1) – алгоритм Евклида.
.
Эта последовательность не может быть
бесконечной. Значит, на каком-то шаге
деления получится остаток =0. Этим и
объясняется последнее равенство (1).
Равенство (1) – алгоритм Евклида.
Т:
ТЕОРЕМА ЕВКЛИДА: Последний не равный
нулю остаток в алгоритме Евклида равен

Докажем, что
Докажем, что
 - общий делитель
.
Следуем по алгоритму Евклида снизу
вверх.
- общий делитель
.
Следуем по алгоритму Евклида снизу
вверх.
 ,
но тогда
,
но тогда
 Пусть
Пусть
 ,
докажем, что
,
докажем, что
 .
По алгоритму Евклида сверху вниз
.
По алгоритму Евклида сверху вниз

Следствие:
Если
 ,
то
,
то
 существует и единственный с точностью
до знака.
Единственность следует из леммы 2. Если
существует и единственный с точностью
до знака.
Единственность следует из леммы 2. Если
 ,
то существование следует из условия
,
то существование следует из условия
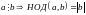 .
Если
.
Если
 ,
то существование НОД следует из алгоритма
Евклида.
,
то существование НОД следует из алгоритма
Евклида.
Пример: Найти НОД(525,231). 1) 525=231*2+63, 2) 231=63*3+42, 3) 63=42*1+21, 4) 42=21*2+0. Ответ: 21.
Т:
О ЛИНЕЙНОМ ВЫРАЖЕНИИ НОД: Если
,
то существуют целые
 такие, что
такие, что
 .
Предположим, что
.
Предположим, что
 .
Пусть
.
Пусть


Пример: Найти линейное выражение НОД(525,231)=21. 21=63+42*
*(–1)=63+(213+63*(–3))*(–1)=231*(–1)+63*(1+3)=231*(–1)+63*4=
=231*(–1)+5251+231*(–2)*4=231*(–1)+525*4+231*(–9);
21=524*4+231*(–9).
Св-во:
–
наименьшее натуральное число
,
которое представимо в виде

 То,
что
То,
что
 выражается в виде
выражается в виде
 доказано ранее в теореме О ЛИНЕЙНОМ
ВЫРАЖЕНИИ.
доказано ранее в теореме О ЛИНЕЙНОМ
ВЫРАЖЕНИИ.
Св-во:
–
наибольший общий делитель чисел
.
Пусть
,
– общий делитель чисел
.
 ,
т.к.
,
т.к.

Наименьшее общее кратное
Опр.:
Пусть
целые ненулевые числа. Целое число
 называют из общим кратным, если
называют из общим кратным, если

Опр.:
 .
Натуральное число
называют наименьшим общим кратным чисел
,
если оно является их общим кратным и
при этом оно делит любое общее кратное
чисел
и
.
Натуральное число
называют наименьшим общим кратным чисел
,
если оно является их общим кратным и
при этом оно делит любое общее кратное
чисел
и

 .
.
Св-во:
Если
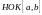 существует, то оно единственное.
существует, то оно единственное.
 общее
кратное
,
но при этом
общее
кратное
,
но при этом
 .
Аналогично получаем, то
.
Аналогично получаем, то

Св-во:
Если
существует, то оно является наименьшим
по величине натуральным числом, которое
кратно и
 ,
и
,
и
 .
Пусть
,
– общее кратное чисел
,
тогда
.
Пусть
,
– общее кратное чисел
,
тогда
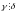

Св-во.:
 при любой комбинации знаков +/–.
при любой комбинации знаков +/–.

Т.:
Формула связи НОК и НОД:
 .
.

 ,
тогда
,
тогда
 – общее кратное.
– общее кратное
,
– общее кратное.
– общее кратное
,
 ,
но
,
но
 ,
тогда по свойству
,
тогда по свойству

Пример:
Найти
 .
.
 .
.
Следствие:
 .
Очевидно.
.
Очевидно.
Св-во:
Пусть
 ,
тогда
,
тогда

 .
1)
.
1)

 2)
2)


