10 Пластическая деформация. Хар-ки деф-ции. Различия относительной и истинной деф-ции при поэтапном растяжении образца

Изменение формы и размеров твердых тел под действием приложенных внешних сил называется деформацией. Деформация пропадающая после снятия внешних сил называется упругой или обратимой.

В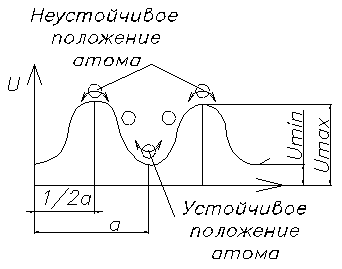 процессе упругой деформации тело аккумулирует потенциальную энергию, которая при разгрузке восстанавливает первоначальные размеры и форму тела. Между атомами твердого тела одновременно действуют силы притяжения и отталкивания, которые удерживают атомы около состояния равновесия и обеспечивают стабильность кристаллической решетки, характеризующейся минимальным значением потенциальной энергии.

U – потенциальная энергия решетки.

r – расстояние между атомами.

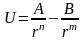(1).

А,В = const = f(природа вещества).

m,n – показатели сил притяжения и сил отталкивания соответственно.

При устойчивом положении атомов расстояние между ними равно параметру решетки. Выражение для измерения потенциальной энергии решетки с изменением расстояния между атомами определяет величину внутренних сил.

.

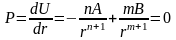Если внутренние силы отсутствуют (атомы расположены в равновесном положении) то последнее выражение записывается также, только в частных производных (вместо d - д). Это значит, что энергия решетки минимальна Umin при r=a. При приложении внешних сил нарушается устойчивое положение атомов, в результате чего повышается потенциальная энергия решетки. Стремление атомов вернутся в устойчивое положение решетки воспринимается как напряженное состояние тела. При разгрузке от внешних сил атомы, отклоненные от положения равновесия возвращаются на свои места. При этом восстанавливаются первоначальные форма и размеры тела. Если после снятия внешних сил тело не приняло первоначальную форму, то имеет место пластическая (необратимая, остаточная) деформация.

Элементарную деформацию можно представить как перенос атомов из одного устойчивого положения в другое на величину межатомного расстояния (параметр решетки). Этому переносу предшествует отклонение атома от равновесного положения. Отсюда следует закон наличия упругой деформации при пластическом формоизменении: всякой пластической деформации предшествует упругая деформация. Сумма упругой и пластической деформации составляет полную деформацию. .

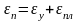В зависимости от вклада каждой из составляющих можно выделить 3 класса деформаций

1) пластическая Eps_y<<Eps_пл

2) упруго-пластическая Eps_y<Eps_пл

4. малоупругие деформации Epsy>Eps_пл.

Вследствие изменения межатомных расстояний под воздействием внешних сил упругая деформация вызывает обратимое изменение объема тел. dV/V=1%. Показателем объемного изменения тела при линейном напряженном состоянии (например при одноосном растяжении тонкого длинного стержня) является число Пуассона 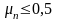. В случае одноосного растяжения стержня его определяют как Eps_c/Eps_p.

.

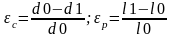d0, l0 – начальные, d1,l1 - конечные диаметр и длина стержня.

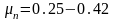, для эластичных материалов – 0,5.

Поскольку при пласт. деф. атомы из одного устойчивого положения переходят в другое и после снятия внешних сил межатомные расстояния восстанавливаются до первоначальных величин, следовательно в результате пласт. деф. не происходит изменения объема тел. Тогда можно записать что для случая пластической деформации коэффициент Пуассона = 0,5.

Упругая деформация характеризуется в основном пропорциональной зависимостью между напряжением и деформацией и описывается законом Гука:

,

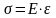где Е – модуль упругости первого рода (модуль Юнга). Е можно рассматривать как условное напряжение в теле при относительной деформации 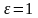и имеет размерность напряжений 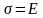. Т.о. E=const, определяющая сопротивление тела упругой деформации. Другим показателем сопротивления упругой деформации является модуль упругости 2-го рода – модуль сдвига.

.

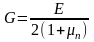Для количественной оценки в-ны формоизменения, а так же пластических характеристик деформированных металлов и сплавов, существует некое математическое выражение, отражающее меру остаточных деформаций.

Абсолютная деформация. Она выражает абсолютное изменение какого-нибудь линейного или углового размера, площади сечения или поверхности выделенного участка тела, либо всего деформированного тела.

, , .

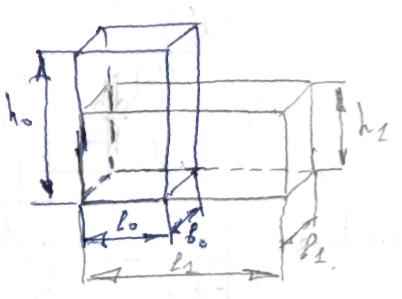
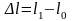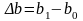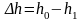Относительная деформация. Характеризует относительное изменение раннее указанных в-н, а именно: , , .

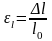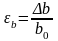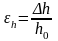Относительную деформацию иногда используют как показатель степени деформации.

Логарифмическая деформация. Является разновидностью относительной.

, , .

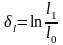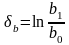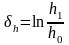Данная деформация обладает свойством адативности, т.е. свойством слагаемости, и может характеризовать суммарную деформацию тела, поэтому ее часто наз. истинной деформацией.

Пусть, например, стержень одноосно растягивается в два приема.

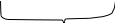
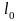
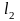
На первом этапе: , .

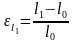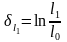На втором этапе: , .

,

,

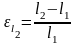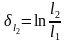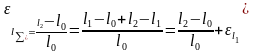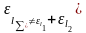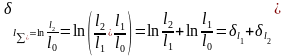
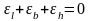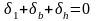Из условия постоянства объема следует, что или . это значит одна из деформаций равна сумме двух других с противоположным знаком. Связь между логарифмическими и относительными деформациями устанавливаются следующим образом:

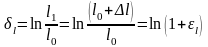
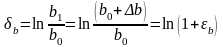
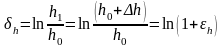
Теория деформаций исследует процесс формоизменения тела используя понятие малых деформаций.

Это позволяет в свою очередь рассматривать процесс формоизменения в каждый данный момент времени. В процессе деформации каждая точка тела смещается от своего первоначального положения. Это в целом характеризует движение сплошной среды. Существует два подхода при изучении движения сплошной среды.