8.Теорема Умова-Пойнтинга. Вектор Пойнтинга
Эта теорема устанавливает энергетические соотношения в электромагнитном поле и направление потока энергии. Рассмотрим малый объем dV в области, занятой электромагнитным полем. В пределах этого объема поле будем считать однородным, т.е. в любой точке объема действуют одинаковые вектора
.
Электромагнитное поле обладает энергией,
плотность которого определяется
выражениями:
- плотность
энергии электрического поля,
– плотность
энергии магнитного поля.
Энергия электромагнитного поля в малом объеме
.
(5.40)
Умножим первое
уравнение Максвелла на
:
.
(5.41)
Умножим второе
уравнение на
:
.
(5.42)
В результате получим
,
(5.43)
.
(5.44)
Вычтем из первого уравнения второе
.
(5.45)
В соответствие с математической формулой
,
(5.46)
преобразуем левую часть:
.
(5.47)
Проинтегрируем уравнение по объему с учетом последнего выражения,
.
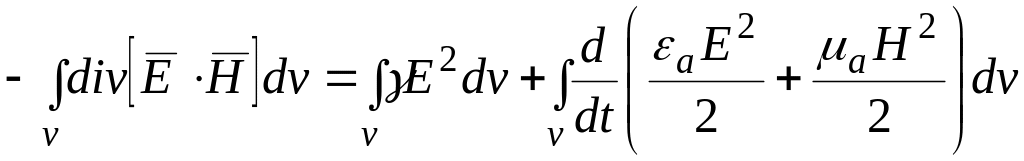(5.48)
Преобразуем левую часть по теореме Остроградского. Первое слагаемое правой части это мощность тепловых потерь в объеме. Во втором слагаемом поменяем местами операции интегрирования и дифференцирования. При этом интеграл дает величину энергии электромагнитного поля в рассматриваемом объеме. С учетом этого получим выражение:
-
.
(5.49)
Это выражение носит название теоремы Умова-Пойнтинга. Подинтегральное выражение
(5.50)
представляет собой вектор и носит название вектора Пойнтинга. Размерность определяется следующим образом.
;
;
.
Таким образом,
вектор
определяет плотность потока энергии,
проходящей в единицу времени через
единичную площадку, расположенную
перпендикулярно движению энергии.
Другими словами, вектор показывает
направление движения энергии в данной
точке. Левая часть теоремы – поток
энергии за единицу времени сквозь
замкнутую поверхность S
, ограничивающую рассматриваемый объем.
Этот поток положителен, если он выходит
из объема, наоборот.
Теорема Умова-Пойнтинга это баланс энергии для объема V , ограниченного поверхностью S. В левой части – количество энергии поступающей извне в данный объем за единицу времени. Правая часть показывает, что эта энергия расходуется на тепловые потери (нагрев) и на изменение энергии электромагнитного поля.