
- •Вопрос1. Основные понятия кинематики.
- •Вопрос2. Скорость и ускорение.
- •Вопрос3. Кинематика вращ. Движения.
- •Вопрос4. 3 закона Ньютона.
- •Вопрос5. Центр масс и его движение. Закон сохранения импульса.
- •Вопрос6. Реактивное движение.
- •Вопрос7. Работа и мощность.
- •Вопрос8. Кинетическая энергия.
- •Вопрос9. Потенциальная энергия.
- •Вопрос10. Закон сохранения механической энергии.
- •Вопрос11. Упругий и неупругий удар шаров.
- •Вопрос12. Уравнение динамики вращательного движения.
- •Вопрос13. Теорема Штейнера.
- •Вопрос14. Работа при вращательном движении.
- •Вопрос15. Кинетическая энергия вращающегося тела.
- •Вопрос16. Закон сохранения момента импульса.
- •Вопрос17. Использование законов сохранения для решения задач.
- •Вопрос18. Гармонические колебательные движения.
- •Вопрос19. Динамика гармонических колебаний.
- •Вопрос20. Физический и математический маятники.
- •Вопрос21. Энергия колебательного движения.
- •Вопрос22. Сложение колебаний одинакового направления.
- •Вопрос23. Сложение взаимно перпендикулярных колебаний.
- •Вопрос24. Затухающие колебания.
- •Вопрос25. Вынужденные колебания. Резонанс.
- •Вопрос26. Распространение упругих волн.
- •Вопрос27. Уравнение плоской сферической волны.
- •Вопрос28. Уравнение плоской волны распространяющейся в произвольном направлении. Волновое уравнение.
- •Вопрос29. Скорость распространения упругих волн.
- •Вопрос30. Энергия упругой волны. Вектор Умова.
- •Вопрос31. Интерференция волн. Стоячие волны.
- •Вопрос32. Звук,ультразвук.
- •Вопрос33. Предмет молекулярной физики. Тепловое движение.
- •Вопрос34.Термодинамические параметры. Уравнение состояния.
- •Вопрос35.Изопроцессы в газах.
- •Вопрос36. Основное уравнение мкт.
- •Вопрос37. Распределение молекул по скоростям Максвелла
- •Вопрос38. Опыт Штерна.
- •Вопрос39. Барометрическая формула распределения Больцмана.
- •Вопрос40. Средняя длина свободного пробега молекул. Эффективный деаметр!
- •Вопрос41. Диффузия.
- •Вопрос42. Теплопроводность.
- •Вопрос43. Вязкость.
- •Вопрос44. Основные понятия и определения термодинамики.
- •Вопрос45. Внутренняя энергия системы тел.
- •Вопрос46.Теплота и работа.
- •Вопрос47. Первое начало термодинамики.
- •Вопрос48. Теплоемкости газов.
- •Вопрос49. Закон Дюлонга и Пти
- •Вопрос50. Уравнение Адиабаты. Политропические процессы.
- •Вопрос51. Работа в изопроцессах.
- •Вопрос52. Кпд тепловых двигателей (второе начало термодинамики)
- •Вопрос53. Цикл Карно.
Вопрос12. Уравнение динамики вращательного движения.
Основное уравнение динамики вращательного движения материальной точки - угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.
М = E*J или E = M/J
Сравнивая полученное выражение со вторым законом Ньютона с поступательным законом, видим, что момент инерции J является мерой инертности тела во вращательном движении. Как и масса величина аддитивная.
Момент инерции тонкого кольца:
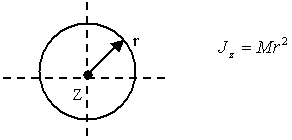
Вопрос13. Теорема Штейнера.
Теоре́ма
Гю́йгенса — Ште́йнера,
или просто теорема
Штейнера (названа
по имени швейцарского математика Якоба
Штейнера и
голландского математика, физика и
астронома Христиана
Гюйгенса): момент
инерции тела ![]() относительно
произвольной оси равен сумме момента
инерции этого тела
относительно
произвольной оси равен сумме момента
инерции этого тела ![]() относительно
параллельной ей оси, проходящей через
центр масс тела, и произведения массы
тела
на
квадрат расстояния
относительно
параллельной ей оси, проходящей через
центр масс тела, и произведения массы
тела
на
квадрат расстояния ![]() между
осями:
между
осями:
![]()
где
— известный момент инерции относительно оси, проходящей через центр масс тела,
— искомый момент инерции относительно параллельной оси,
— масса тела,
— расстояние между указанными осями.
Момент инерции, по определению:
![]()
Радиус-вектор ![]() можно
расписать как разность двух векторов:
можно
расписать как разность двух векторов:
![]() ,
,
где ![]() —
радиус-вектор расстояния между старой
и новой осью вращения. Тогда выражение
для момента инерции примет вид:
—
радиус-вектор расстояния между старой
и новой осью вращения. Тогда выражение
для момента инерции примет вид:
![]()
Вынося за сумму , получим:
![]()
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:
![]()
Тогда:
![]()
Откуда и следует искомая формула:
,
где — известный момент инерции относительно оси, проходящей через центр масс тела.
Вопрос14. Работа при вращательном движении.
Часто встречаются детали машин, вращающиеся вокруг неподвижных осей. Причиной вращательного движения является приложенный к телу вращающий момент относительно оси, который создается парой сил или силой F
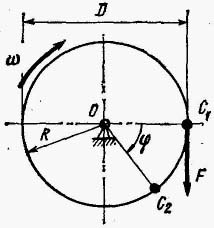
и определяется по формуле
![]()
При повороте тела на малый угол dφ работа совершается силой F, точка приложения которой перемещается из положения С1 в положение С2. Полное перемещение точки приложения силы равно длине дуги радиусом R:
![]()
Так как сила F все время направлена по касательной к перемещению s, то совершаемая ею работа определится как произведение силы на перемещение:
![]()
Произведение
силы на радиус определяет вращающий
момент, т. е. ![]() .
Учитывая это, окончательно находим dW
= М dφ.
Интегрируя, получим:
.
Учитывая это, окончательно находим dW
= М dφ.
Интегрируя, получим:
![]()
Работа вращающего момента равна произведению момента на угол поворота.
Определим мощность при вращательном движении
![]()
Вопрос15. Кинетическая энергия вращающегося тела.
Кинетическая энергия – величина аддитивная. Поэтому кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех nматериальных точек, на которые это тело можно мысленно разбить:
|
|
|
Если
тело вращается вокруг неподвижной
оси z с
угловой скоростью ![]() ,
то линейная скорость i-й
точки
,
то линейная скорость i-й
точки ![]() , Ri –
расстояние до оси вращения. Следовательно,
, Ri –
расстояние до оси вращения. Следовательно,
|
|
|
|
Сопоставив обе формулы, можно увидеть, что момент инерции тела l является мерой инертности при вращательном движении, так же как масса m – мера инерции при поступательном движении. В общем случае движение твердого тела можно представить в виде суммы двух движений – поступательного со скоростью vc и вращательного с угловой скоростью ω вокруг мгновенной оси, проходящей через центр инерции. Тогда полная кинетическая энергия этого тела
|
|
|
|
Здесь Ic – момент инерции относительно мгновенной оси вращения, проходящей через центр инерции.
