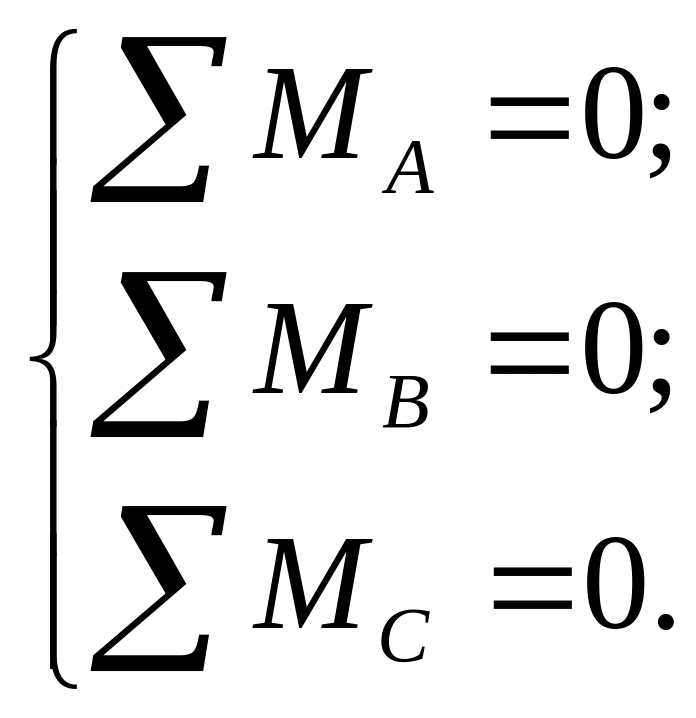47: Червячные передачи. Усилия в зацеплении. Основы расчета на прочность.

Червячная передача относится к числу так называемых зубча­то-винтовых, т. е. имеющих признаки, характерные и для зубча­тых, и для винтовых передач.

Основные достоинства червячной передачи, обусловившие ее широкое распространение в различных отраслях машиностроения:

1. Плавность и бесшумность работы;

2. Возможность получения больших передаточных чисел при сравнительно небольших габаритах передачи. Червячные пере­дачи применяются с передаточными числами от u = 5 до u = 500. Диапазон передаточных чисел, применяемых в силовых передачах, u = 10-80 (в редких случаях до 120).

3. Компактность.

Недостатки червячной передачи:

1. Сравнительно невысокий к.п.д.

2. Сильный нагрев передачи вследствие перехода потерь на трение в тепловую энергию. Для уменьшения нагрева в червячной передаче применяют масляные резервуары с ребристыми стенками с целью более интенсивной теплоотдачи в окружающий воздух, обдув корпуса и другие способы охлаждения.

3. Небольшие передаваемые мощности.

Червячные передачи различают по числу заходов червяка — одно-, двух-, трех- и многозаходные; по расположению вала чер­вяка — относительно червячного колеса с верхним, нижним и боковым расположениями.

Усилия, действующие в зацеплении

d₁,d₂ – делительные диаметры червяка и колеса соответственно.

Особенности расчета червячных передач

Проектный расчет на контактную прочность строится на основе определения межосевого расстояния

Проверочный расчет на изгиб

1,2 – коэффициент упрочнения зуба за счет его длины и дугообразности.

у – коэффициент формы зуба.

48: Кинематический анализ рычажных механизмов.

Кинематический анализ рычажных механизмов предусматривает определение положения звеньев и построение траектории движения отдельных точек механизма. Определение линейных скоростей точек и угловых скоростей звеньев механизма, ускорений точек и угловых ускорений звеньев механизма.

1. Определение положения звеньев.

Рис. 1

Используя начальные условия определяем положение точки С

2. Определение скоростей.

Дифференцируя любой угол по , получаем безразмерную скорость /или ее аналог/. Связь между действительной угловой скоростью и ее аналогом можно записать в следующем виде:

Аналогично и для линейной скорости:

Дифференцируя по систему (1) и умножая на угловую скорость 1 звена, получим систему 2:

Первое уравнение из системы (2) определяет линейную скорость точки С, а из второго уравнения можно определить угловую скорость второго звена:

Вводя аналог ускорения аналогичным образом определяется ускорение точки С и угловое ускорение второго звена:

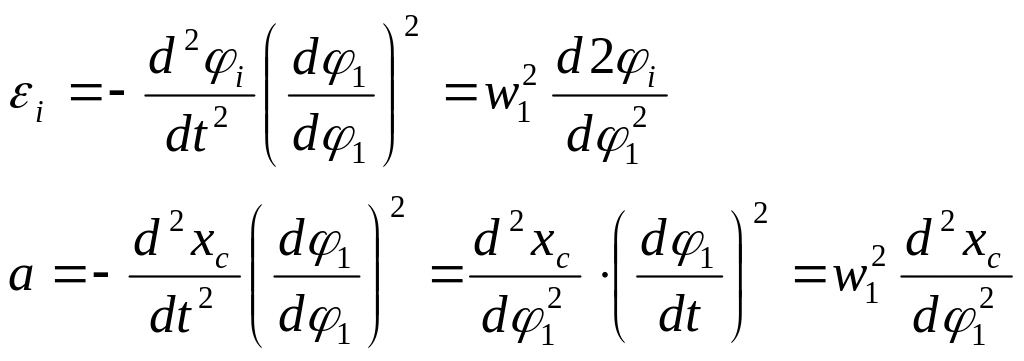
В системе 2 переменными являются не только φ₂, но и w₂

Из второго уравнения третьей системы можно найти угловое уравнение третьего звена .

50: Главный вектор и главный момент. Приведение системы сил к простейшему виду.

Пусть к телу в точке А, В и С приложена плоская система сил (Р1,Р2,Р3) (Рис 7) при параллельном переносе этих сил в точку О получается новая плоская система сил (Р1’,Р2’,Р3’) а также система пар сил Р₁ Р’’₁ ; Р₂ Р’’₂ ; Р₃ Р’’₃ ; эти пары сил можно определить в следующих зависимостях М (Р₁)= Р₁*а, М (Р₂)= Р₂*b, М (Р₃)= Р₃*c.

Главный вектор новой системы сил равен геометрической сумме векторов системы приведенных с к точке 0.

Главный момент системы относительно заданной точки О, равен сумме моментов сил, относительно той же точки.

Произвольная плоская система сил (Р1,Р2,Р3) эквивалентна силе приложенной в точке О и равна главному вектору , а так же паре сил с моментом (главный момент системы).

Приведение плоской системы к простому виду.

1. Выбрать систему координат

2. Выбрать центр приведения

3. Вычислить проекции главного вектора на координатные оси (V_x ,V_y)

4. Вычислить модуль главного вектора

5. Вычислить главный момент.

Возможны следующие виды при приведении к простому виду

1. V и М₀ не равны 0, в этом случае равнодействующая равнаV который отстоит от равнодействующей на величину h где h= М₀ /V

2. V не равна 0, М₀ равна 0 система приводится к равнодействующей при этом R=V и совпадает с линией вектора

3. V равна 0, М₀ не равна 0 – система приводится к паре сил с иоиентом равному главному моменту

4. V =М₀ = 0 – в этом случае система находится в равновесии для уравнения равновесия сил произвольно расположенных на плоскости V и М₀ должны быть равны 0, в связи с этим реализуется несколько форм равновесия

а) б)