45. Теорема об изменении кинетической энергии Основы динамики точки и тела. Динамика механизмов.

1. Понятия и определения.

Основными задачами динамики являются:

1. По известному закону движения определить действующие силы.

2. Зная действующие силы и начальные условия, определить закон движения (тела, точки, механизма).

Аксиомы динамики

1. Всякая свободная от внешнего воздействия материальная точка сохраняет свое состояние покоя или равномерного движения, до тех пор, пока к этой точке или телу не будет приложена сила.

2. Модуль силы, действующей на материальную точку, равен произведению массы этой точки, на модуль ускорения. Направление действия силы, совпадает с направлением ускорения.

3. Две материальные точки действуют друг на друга с силами равными по модулю и противоположными по направлению, вдоль прямой, соединяющей их центры.

4. Если на материальную точку действует одновременно несколько сил, то каждая из них сообщает точке ускорение, модуль которого равен модулю этой силы, деленному на массу этой точки.

Тогда для системы сил, ускорение будет определяться суммой сил, деленных на массу этой точки:

.

Работа. Мощность. Кинетическая энергия.

На прямолинейном участке .

Для криволинейного участка , где α – угол между направлениями перемещения и силы.( )

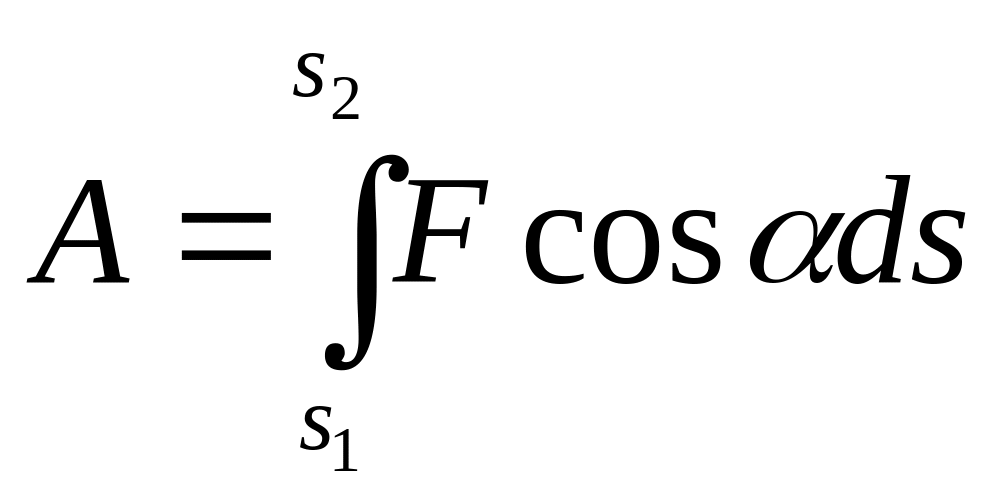
Выражение для работы по перемещению тела под действием силы, на конечном криволинейном участке, с учетом криволинейной траектории, в декартовой системе координат может быть записано следующим образом:

.

Выражение для мощности при поступательном движении имеет следующий вид:

, при вращательном движении , где Т_с – сила сопротивления.

Кинетическая энергия поступательного движения определится по формуле:

Если имеется система точек, то их общая энергия:

, где М – масса тела, состоящего из нескольких точек, а V_C – скорость центра масс.

Энергия системы точек при вращательном движении может быть определена по формуле:

w- угловая скорость точек относительно центра масс.

Т. К. то

Для различных тел различны моменты инерции.

Так для диска , а для кольца .

Теорема об изменении кинетической энергии.

Изменение кинетической энергии материальной точки за некоторый промежуток времени равен работе, приложенных к этой точке сил, затраченной на перемещение этой точки за этот промежуток времени.

(1)

Проектируем вектор силы на вектор скорости:

(2)

Интегрируя последнее выражение в пределах от V₀ до V, получим:

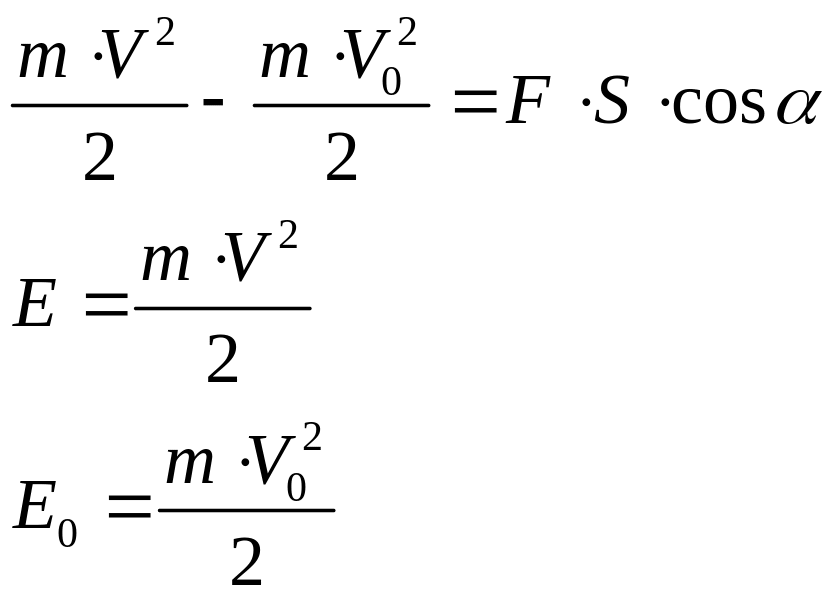Изменение кинетической энергии:

.

Теорема об изменении кинетической энергии показывает, что эффект действия силы, выражающийся в изменении кинетической энергии материальной точки, измеряется работой этой силы.

Для системы, состоящей из n точек, эта теорема может быть записана следующим образом:

.

Для системы точек вводится понятие центра масс. Так в декартовой системе координат, координаты центра масс можно записать в следующем виде:

46: Основы кинетостатики. Принцип Даламбера.

Принцип Даламбера

Пусть материальная точка М совершает движение с ускорением. На эту точку действует сила и равнодействующая сил реакции связи R. Добавим силу инерции точки М - Ф.

F= .

Для данной системы запишем условие равновесия, с учетом силы инерции.

Тогда сила инерции определится как:

Принцип: Если к действующим на точку активным силам и реакциям добавить силу инерции, то в каждый момент времени полученная система сил будет уравновешена.

Принцип Даламбера представляет собой формальный математический прием, удобный для решения задач динамики. Этот прием позволяет записывать динамические уравнения движения в форме уравнений равновесия.

Особенности:

При криволинейном движении:

Для системы внешних и внутренних сил, принцип Даламбера может быть представлен в следующем виде:

(1)

где - сумма внешних сил,

- сумма внутренних сил,

- сумма сил инерции.

Принцип Даламбера может быть записан и для моментов сил:

(2)

В механике макрообъектов внутренние силы считаются уравновешенными, и с учетом этого можем считать:

Можно принять, что силы и моменты инерции, представляются главным вектором и главным моментом сил инерции:

В проекциях на оси координат получают уравнения, аналогичные уравнениям статики:

Для пространственной системы:

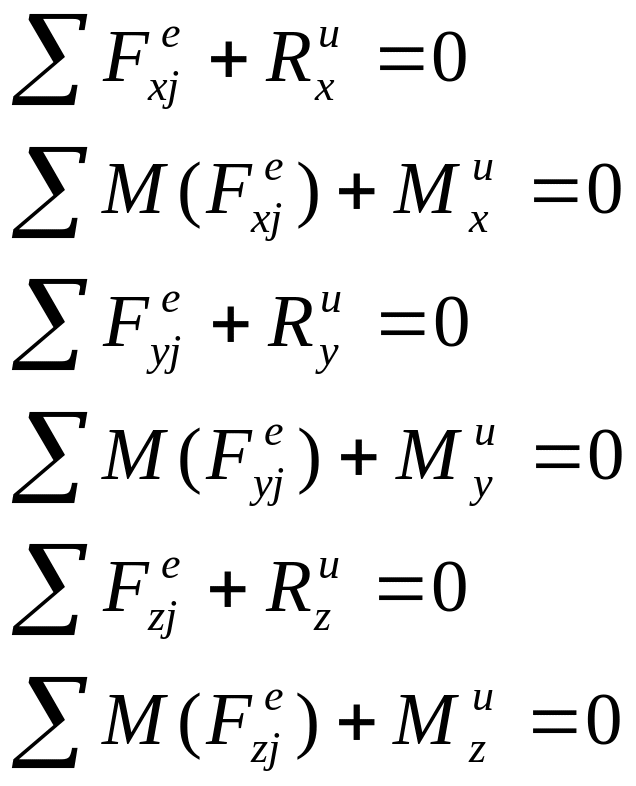
Для плоской системы:

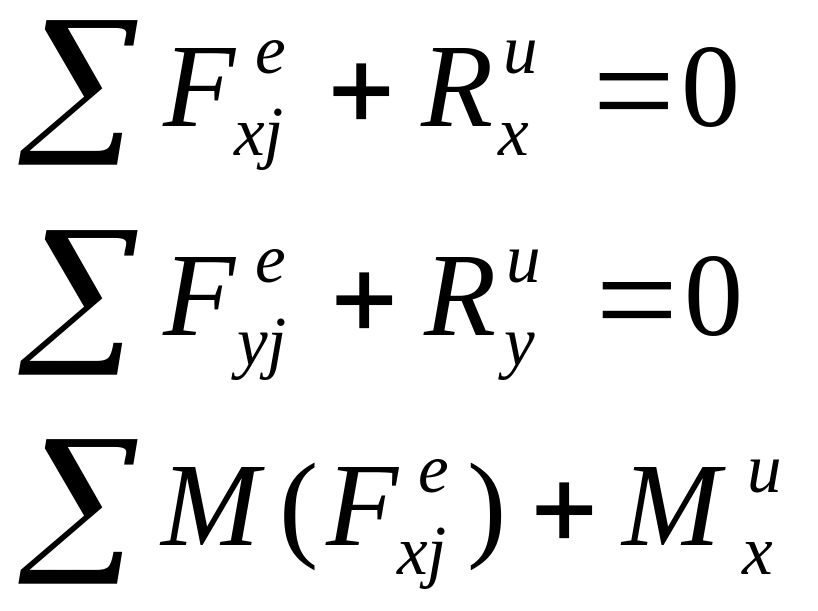
Расчеты при динамических нагрузках.

Если известны действующие силы и силы инерции, возможно использование метода сечений и уравнения равновесия.

Силы инерции вызывают в элементах конструкции дополнительные нагрузки и соответствующие напряжения. Для простоты эти напряжения можно считать статическими, но вызванными силами инерции.

Для решения задач прочности связанными с динамическими нагрузками:

1. Определение ускорения точек;

2. Определение сил инерции;

3. Элемент (конструкция) нагружается силами инерции и внешними силами;

4. Расчеты ведутся по аналогии с расчетом статических систем.

Пример: Требуется определить напряжение в тросе на расстоянии z от его конца. (Рис. 1).

уравнение равновесия

Определение массы поднимаемой системы

Определение силы инерции

Определяем усилия, действующие на тросс

- объемный вес материала троса, А – площадь поперечного сечения троса.

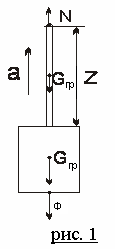
Допускаемое напряжение с учетом зависимости (1) может быть представлено в следующем виде: