2.9 Расчет эл-х цепей в установившемся гармоническом режиме…

3.1 Понятие переходного процесса. Дифференциальное ур-е переходного процесса, тип диф ур-я и его вывод с помощью з-нов Кирхгофа

Рассмотрим эл цепь состоящую из резисторов, катушек, конденсаторов, ист напряжения и ист тока.

Все источники явл-ся либо постоянными либо периодическими, примем период Ту всех ист-ов во 2-м случаем одинаковым.

Будем считать, что рабата ист-ка началась при t=-∞, тогда к моменту времени t=0 в цепи будет иметь место установившийся режим. Это означает, что токи во всех ветвях цепи и напряжения на всех эл-тах будет изменяться во времени по периодическому з-ну с одинаковым для всех величин периодом T. Пусть в момент t=0 в цепи происходит коммутация: включ каких-то источников, или подключ новых источников, или изменение структуры цепи. Тогда при t→+∞ в цепи возникает новый установившийся режим: токи и напряжения станут опять периодическими с тем же общим периодом Т, но графики этих ф-ций будут отличаться от тех, что были до коммутации. Процессы, которые будут происходить в цепи после коммутации, т.е. начиная с t=0 , называют переходными процессами

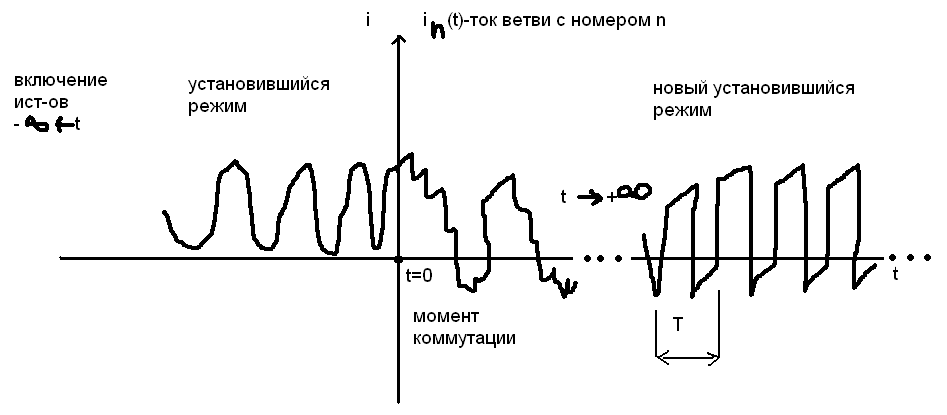
Дифференциальное ур-е переходного процесса – так мы будем называть диф-е ур-я для некоторого выделенного нами тока ветви или напряжения на элементе.

Эти ур-я составляют для цепи, возникшей после коммутации.

Делается это так:

а) записывают полную сис-му ур-й по 1-му и 2-му з-нам Кирхгофа для данной цепи.

б) исключая последовательно из сис-мы неизвестные кроме 1-ой получают искомое ур-е. будет выглядеть ток(искомой величиной здесь будем считать ток i в некоторой ветви):

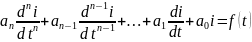- дифф ур-е переходного процесса

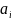(i= - коэфф ур-я (некоторые числа, котор выражаются через параметры эл-тов цепи)

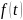-свободный член(вид этой ф-ции определяется имеющимися в цепи источниками)

Натуральное число n наз-ся порядком дифф ур-я.

Тип этого дифф ур-я:

- обыкновенное

- линейное

- с пост коэфф

- неоднородное(правая часть отлична от 0, если =0, то ур-е наз-ся однородным).

Рассмотрим на примере как получается такое ур-е:

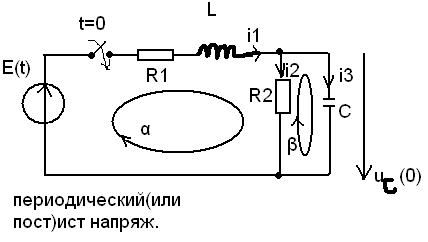
Для цепи после коммутации имеем:

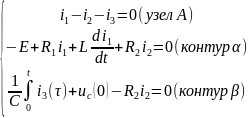
Дифф-ем 3-е ур-е получим новую сис-му:

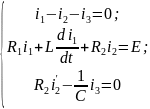
Составим ур-е для тока 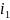, подставляя в 1-е ур-е из 3-го ток 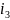получим новую сис-му:

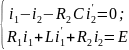
Из 2-го ур-я найдём ток :

;

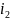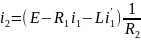После дифф-я этого ур-я будем иметь:

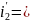
Подставим и 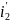в 1-е ур-е.

После преобразований получим такой итог:

- дифф-е ур-е переходного процесса(для тока )

3.2 постановка задачи Каши для линейного дифф ур-я с пост.коэфф. начальные условия. Проблема пересчета начальных условий от t=-0 к t=+0. Правила коммутации.

Дифф-е ур-е переходного процесса

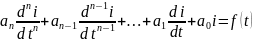(1)

имеет бесконечно много решений. Добавим к нему начальные условия – значения искомой ф-ции и ее первых производных до (n-1) порядка включительно при t=0:

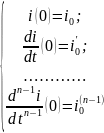(2) некоторые заданные числа(откуда их взять? см ниже!)

Дифф ур-е (1) с начальн условием (2) наз-ся задачей Каши для данного ур-я. Как известно, эта задача имеет единственное решение.

Построив это решение, мы решим задачу о переходном процессе.

Как построить это решение мы рассмотрим в след п., а сейчас вычислим как работа пост 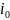, 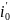и т.д. , входящие в нач условие (2). Прежде всего отметим, что мы должны различать знач-я ф-ций при t→-0(в пределе к о слева до коммутации) и при t→+0(в пределах к 0 справа после коммутации).

Дифф ур-е процесса (1) будет выполняться, начиная с момента t=+0, поэтому в начальных условиях (2) на самом деле подразумевается момент t=+0.

Но известным состоянием цепи явл-ся ее состояние при t=-0, поэтому возникают проблемы пересчета состояния цепи от момента t=-0 к моменту t=+0. При таком подсчете важными оказываются правила коммутации.

Сформулируем 1-ое правило. Рассмотрим подключение RC цепи к источнику пост напряжения

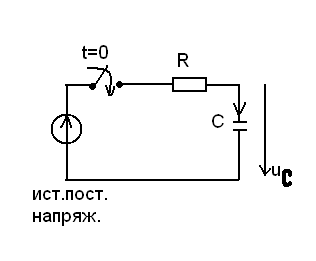
Предположим, что в момент коммутации напряжение на конденсаторе изменяется мгновенно, т.е. ф-ция при t=0 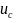(t) имеет разрыв 1-го рода.

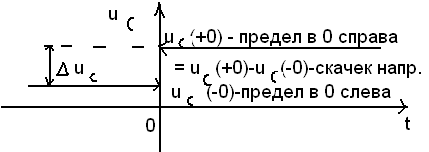
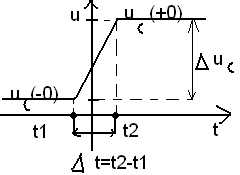
Чтобы увидеть проблему заменим мгновенное изменение напряжения быстрым изменением за время △t

Тогда по 2-му з-ну Кирхгофа для нашей цепи получим:

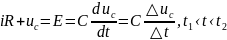(3), где

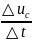-как производная линейной ф-ции,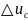 -const, 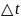→∞=>∞ при →0

Мы видим, что при →0 выполнить рав-во (3) невозможно, т.е. мы приходим к противоречию со 2-м з-ном Кирхгофа.

Отсюда мы получаем 1-е правило коммутации:

Напряжение на конденсаторе мгновенно изменяться не может:

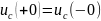
Аналогично выводится 2-е правило коммутации:

Ток через катушку индуктивности мгновенно измениться не может:

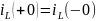
Решение задачи Каши. Имеем при t>0 задачу Каши для обыкновенного линейного неоднородного дифф-го ур-я порядка n с пост коэфф.

n=2

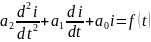(1), t>0 исходное неоднородное ур-е(после коммутации)

1 -я производная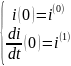 (2)наход-ся по известному сост-ю цепи при t=-0 с помощ з-нов коммут

Имеем ввиду +0! Порядок производной