1.4 Расчёт электрических цепей с помощью законов Кирхгофа…
Составим уравнение по первому закону Кирхгофа для всех узлов кроме одного (будет y=1), и уравнение по 2 закону Кирхгофа для всех независимых контуров (будет К уравнений).Получим систему ленейных алгебраических уравнений (СЛАУ) относительно В неизвестных токов ветвей.
а) В полученной системе число уравнений всегда будет равно числу неизвестных(СЛАУ будет квадратной), это означает , что (Y – 1)+К
(Y-1)+К=В - число ветвей = числу неизвестных токов.
б)Эта квадратное СЛАУ всегда имеет решение, причём единственное.
Найдём все неизвестные токи.
А,В,С – узлы
1,2,3,4,5, - ветви
α,β,γ – независимые контуры
В этой цепи В = 5,Y = 3, К = 3
Составляем систему уравнений по законам Кирхгофа.
По первому закону Кирхгофа:
По второму закону Кирхгофа:
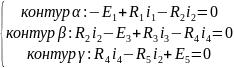
Получим 5 уравнений с 5-ю неизвестными. Приведём эту систему к стандартному виду
Замечание: метод Кирхгофа самый трудоёмкий, он приводит к сис-ме с: В=(У-1)+К неизвестным
1.5 Методы решения квадратных слау…
В общем случае квадратному СЛАУ c n неизвестными выглядит так :
(1)
-коэфф
сис-мы
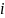-номер
ур-я
-номер
неизв-го
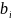-свободн-е
члены
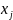-неизв-е,
котор-е нужно найти
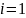,̄n,
j=
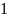,̄n
Квадратную табл из коэфф этой сис-мы:
=
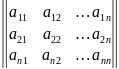(2)
называется основной матрицей системы (1)
определитель или детерминант - есть число которое находится по определенному правилу
определитель
обозначают det
A, ∆ или
Правило для нахождения определителя выглядит так:
n=2
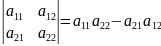
Расчет эл-ких цепей методом контурных токов…
1.Выбираем систему независимых контуров и направление обхода для каждого из них.
2.Вводим контурные токи(вспомогательные фиктивные величины), которые циркулируют во всех контурах по направлению обхода.
3.Составляем для каждого контура уравнение по 2 закону Кирхгофа, считая что во внешних ветвях токи совпадают с контурными, а во внутренних ветвях тики равны алгебраической сумме контурных токов.
4.Решая полученную квадратичную СЛАУ находим контурные токи.
5.Вводим для каждой ветви направление отсчета для фактических токов и выражаем их через контурные.
1.7Узловые напряж и узловые потенциалы…
Л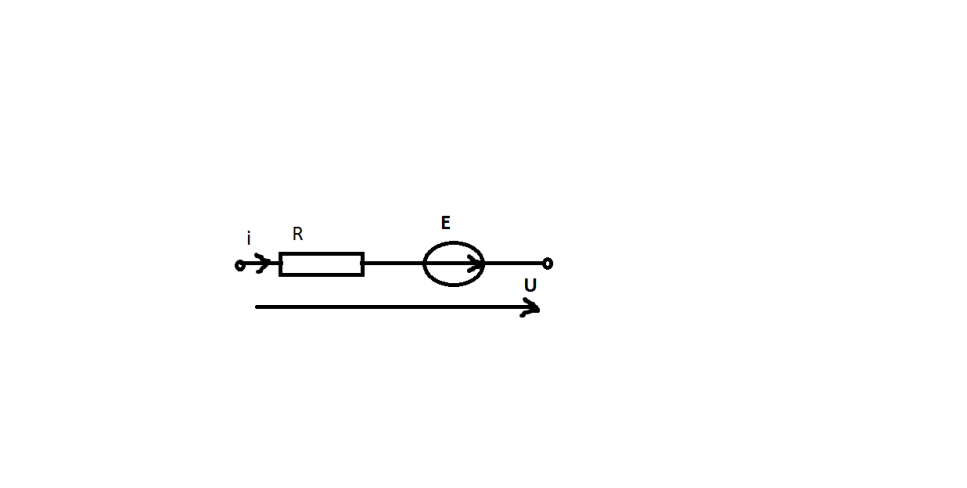
юбая
ветвь цепи состоит из: идеального
источника напряж и идеального резистора
. Связь между " i
" и "U"
называется обобщенным
законом Ома.
*Стрелка для E дана по условию, остальные стрелки установлены случайно. iR-E=U (1) (или iR+E=U если U направлено в другую сторону).
В
методе к которому мы приступаем вместо
напряжений
между узлами(узловое напряжение)
U
вводя потенциалы
узлов(узловые потенциалы)
.
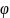Связь между старыми и новыми переменными
такая: U=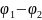
(2)
(если U
направлено от
к
,
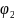иначе U=
-
).
Используя потенциалы формулу (1) можно
представить так: i=
Пусть
цепь имеет n
узлов, тогда по 1 закону Кирхгофа можно
составить n-1
линейно независимых уравнений. Поскольку
токи не изменяются если все потенциалы
одновременно увеличить или уменьшить
на одну и ту же величину, то 1 из потенциалов
можно принять за 0,
в результате получим квадратное слау
относительно
,
, ...,
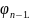
Вид системы: (3)
...-
=
...-
=
...........................................................
...+
=
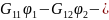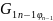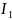
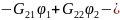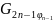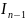
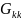-сумма
проводимости ветвей сходящихся в узле,
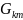-сумма
проводимостей на ветви между k
и m
узлами. Если между узлами ветвь отсутствует
то
=0.В
формировании тока
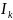участвуют только те ветви которые
содержат напряжение. Если стрелка ист.
напряжения направлена к узлу то вклад
=
,
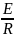в противном случае =
.
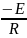Поскольку
и
равны
то основание матрицы системы является
симметричной. Далее решая (3)
найдем
,
, ...,
.
После по уравнению (2) посчитаем токи во
всех ветвях(нужно выбрать направление
отсчета).