
- •1.Дифракционный интеграл.Граничные условия Кирхгофа
- •1.Диффракция Фраунгофера (дифракционная решетка).
- •Дифракция Фраунгофера в геометрически сопряженных плоскостях.
- •Дифракция Фраунгофера на щели и круглом отверстии .
- •Свойства среды с отрицательным коэффициентом поглощения.
- •1.АТеорема Ван Циттера-цернике.
- •Вероятностный анализ квантовых систем. Коэффициенты Эйнштейна.
- •Дифракция Кирхгофа, Френеля и Фраунгофера.
- •Физический смысл Коэффициенты Эйнштейна
- •1) U(p1) на σ равно u(p1); 2) u(p1) на σ равно 0.
- •Теория дифракции Кирхгофа. Граничные условия. Дифракционный интеграл.
- •1) U(p1) на σ равно u(p1); 2) u(p1) на σ равно 0.
- •2.Среда с отрицательным коэффициентом поглощения. Ее свойства.
- •1.Дифракция на непрерывных периодических и не периодических структурах
Дифракция Кирхгофа, Френеля и Фраунгофера.

Дифракция Френеля возникает, когда источник, диафрагма и приемник расположены близко друг от друга. В этом случае нельзя пренебрегать кривизной волн от источника, и приемник будет регистрировать явление дифракции Френеля .Зонная пластинка Френеля , увеличивающая за счет дифракции энергетическую освещенность в точке наблюдения подобно собирающей (положительной) линзе, в качестве рентгенооптического элемента была предложена в 1952 г. Такие пластинки служат основным узлом в сканирующих и изображающих рентгеновских микроскопах с использованием синхротронного излучения.
Дифракция Френеля зависит от зон Френеля , в случае с круглой диафрагмой, мы имеем в виду окружности. Эти окружности имеют определенные характеристики. Их диаметр и толщина расчитываются таким образом, чтобы свет, дифрагируя на них, при попадании на фотопленку усиливался. (В случае с обычными волнами на воде, волны могут усилить друг друга, если попадают в фазу- горб одной накладывается на горб другой). Таким образом, диаметр и толщина окружностей будет зависеть от длины волны и расстояния от пластины до пленки.
Физический смысл Коэффициенты Эйнштейна
Билет №10
1.Граничные условия Кирхгофа.
Граничные условия Кирхгофа :
1) U(p1) на σ равно u(p1); 2) u(p1) на σ равно 0.
Подставляя в G(P1) и заменяя
получим:
![]()
Теперь предположим, что на отверстие Х падает волна от точечного источника:
тогда
Хотя интеграл Френеля- Кирхгофа и дает, в принципе, верный результат, существует одно противоречие:

2.Комплексная функция и комплесная степень когерентности квазимонохроматических волн
Билет №11
Теория дифракции Кирхгофа. Граничные условия. Дифракционный интеграл.


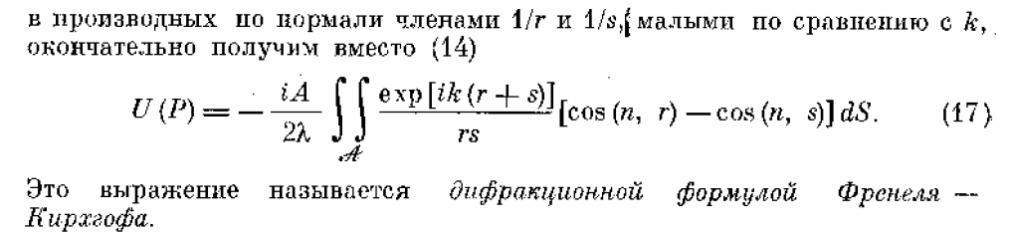
Граничные условия Кирхгофа :
1) U(p1) на σ равно u(p1); 2) u(p1) на σ равно 0.
Подставляя в G(P1) и заменяя
Теперь предположим, что на отверстие Х падает волна от точечного источника:
тогда
2.Взаимная
интенсивность. Комплексная степень
интенсивности.
В не входит взаимная интенсивность , образованная наложением волновых полей, прошедших через различные участки апертуры, т.к. при указанном выше усреднении она стремится к нулю.

При выводе (12) учитывалась только та интенсивность , которая вносит вклад в образование интерференционной картины, т.е. учитывалась взаимная интенсивность , которая после соответствущей нормировки переходит в функцию взаимной когерентности для диффузно-когерентного излучения и, следовательно, совпадает с трехмерным распределением комплексной амплитуды вблизи фокуса.
2.Б Вычисление интенсивности в дифракционном поле производится по формуле:
![]()
где i(p1) i(Р2)- интенсивности на произвольных бесконечно малых площадках dp1, dp2 с центрами в точках Р1 и Р2; γ(Π1,Р2,0)- комплексная степень пространственной когерентности между волнами, исходящими из точек Р1 и Р2; - волновое число; -расстояние от апертуры до плоскости наблюдения; с0 - постоянная, зависящая от размеров апертуры; А - площадь апертуры.
Задача определения
комплексной степени пространственной
когерентности математически сводится
к решению интегрального уравнения (2).
Для излучения лазера эта задача решена
в работах /5,6/, в которых показано, что
![]()
где i (q)- интенсивность в дифракционной поле, iа(Р)- интенсивность на апертуре.
Из выражения (3) видно, что определение комплексной степени пространственной когерентности экспериментально производится с помощью измерения интенсивностей в дифракционном поле и на апертуре.
Билет № 12
