
- •11) Функция распределения (ф.Р.) одномерной с.В. И её свойства.
- •23) Законы распределения отдельных с.В., входящих в систему. Условные з.Р. Зависимость с.В.
- •24) Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции.
- •25) Нормальный закон на плоскости
- •29) Математическое ожидание и дисперсия неслучайной величины. Вынос постоянного множителя.
- •30) Математическое ожидание и дисперсия суммы случайных величин.
- •31) Математическое ожидание и дисперсия произведения случайных величин.
- •35) Системы произвольного числа нормальных законов на плоскости. Корреляционная матрица.
- •36) Матожидание и дисперсия для линейной функции случайных аргументов.
- •37) Закон больших чисел. Неравенство Чебышева.
- •38) Теорема Маркова.
- •39) Теорема Чебышева
- •40) Теорема Бернулли.
- •45) Статистические оценки матожидания и дисперсии. Метод моментов.
- •46) Доверительная вероятность. Доверительный интервал.
- •47) Аппроксимация статистических рядов.
- •48) Критерий согласия Пирсона.
- •49) Критерий согласия Колмогорова
- •50) Случайные процессы.
47) Аппроксимация статистических рядов.
Одним из основных методов аппроксимации статистических рядов является м.н.к.
Пусть производится опыт, целью которого является, исследование зависимости некоторой физической величины y от физической величины x. Предполагается, что величины x и y связаны функциональной зависимостью.
Вид этой зависимости и требуется определить из опыта.
Предположим, что в результате опыта мы получили ряд экспериментальных точек и построили график зависимости y от x.
Метод основан на минимизации суммы квадратов отклонений наблюденных значений yi от φ(xi):
 .
.
Перейдем
к задаче определения параметров
![]() ,
исходя из принципа наименьших квадратов.
Пусть имеется таблица экспериментальных
данных (табл. 14.8.1) и пусть из каких-то
соображений (связанных с существом
явления или просто с внешним видом
наблюденной зависимости) выбран общий
вид функции
,
зависящей от нескольких числовых
параметров
;
именно эти параметры и требуется выбрать
согласно методу наименьших квадратов
так, чтобы сумма квадратов отклонений
,
исходя из принципа наименьших квадратов.
Пусть имеется таблица экспериментальных
данных (табл. 14.8.1) и пусть из каких-то
соображений (связанных с существом
явления или просто с внешним видом
наблюденной зависимости) выбран общий
вид функции
,
зависящей от нескольких числовых
параметров
;
именно эти параметры и требуется выбрать
согласно методу наименьших квадратов
так, чтобы сумма квадратов отклонений
![]() от
от
![]() была
минимальна. Запишем
была
минимальна. Запишем
![]() как
функцию не только аргумента
,
но и параметров
как
функцию не только аргумента
,
но и параметров
![]() . Требуется
выбрать
так,
чтобы выполнялось условие:
. Требуется
выбрать
так,
чтобы выполнялось условие:
 .
.
Найдем значения , обращающие левую часть выражения (14.8.6) в минимум. Для этого продифференцируем ее по и приравняем производные нулю:

48) Критерий согласия Пирсона.
Критерий
согласия
 – Пирсона. Этот метод применим как к
непрерывным, так и к дискретным
распределениям. Кроме того, допускается
в гипотетическом распределении
использовать в качестве значений
параметров их оценки.
– Пирсона. Этот метод применим как к
непрерывным, так и к дискретным
распределениям. Кроме того, допускается
в гипотетическом распределении
использовать в качестве значений
параметров их оценки.
В
соответствии с этим методом область
возможных значений случайной величины
разбивается на k разрядов
и для каждого из них находится количество
m элементов выборки,
попавших в разряд, и вычисляется, в
соответствии с генерируемым распределением,
математическое ожидание этого числа
 ,
где
,
где
 – вероятность попадания в i-й
разряд. Пирсон показал, что случайная
величина, определяемая выражением
– вероятность попадания в i-й
разряд. Пирсон показал, что случайная
величина, определяемая выражением при
при
 стремится к
– распределению с (k-1)-й
степенью свободы, если гипотетическое
распределение задано полностью. Если
же s параметров гипотетического
распределения заданы их оценками,
найденными по той же выборке, что и
,
то число степеней свободы критерия
равно k-s-1.
Выборочное распределение признается
согласующимся с генерируемым с
доверительной вероятностью q,
если
стремится к
– распределению с (k-1)-й
степенью свободы, если гипотетическое
распределение задано полностью. Если
же s параметров гипотетического
распределения заданы их оценками,
найденными по той же выборке, что и
,
то число степеней свободы критерия
равно k-s-1.
Выборочное распределение признается
согласующимся с генерируемым с
доверительной вероятностью q,
если
 ,
где
,
где
 – квантиль уровня (1-q)
распределения с (k-s-1)-й
степенью свободы, а
– квантиль уровня (1-q)
распределения с (k-s-1)-й
степенью свободы, а
 – экспериментальное значение критерия.
– экспериментальное значение критерия.
49) Критерий согласия Колмогорова
Этот
метод очень прост, но его применение
требует выполнения двух ограничений:
во-первых, распределение должно быть
непрерывным и, во-вторых, параметры
проверяемого распределения должны быть
известны и не могут быть заменены их
оценками, получаемыми на основе
наблюдений. В качестве меры близости
статистического (выборочного) и
генерируемого распределений принимается
максимальное значение разности их
функций распределения
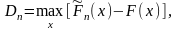
где
 – выборочная функция распределения;
– выборочная функция распределения;
 – генерируемое распределение.
– генерируемое распределение.
Колмогоровым
было показано, что при увеличении объема
выборки n, распределение
случайной величины
 стремится к виду
стремится к виду

На этом основании с доверительной вероятностью q можно утверждать, что выборочное распределение согласуется с гипотетическим, если

где
 –
квантиль распределения уровня (1-q);
–
квантиль распределения уровня (1-q);
 –экспериментально вычисленное значение
–экспериментально вычисленное значение
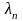 .
.
При использовании этим критерием необходимо иметь в виду, что распределение Колмогорова F(λ) является предельным при и, следовательно, надежные суждения о качестве генерации можно делать лишь по выборкам достаточно большого объема.
