1) Категория случайных явлений. Виды событий. Случайные события. Отношения между событиями.

Под «Событием» в теории вероятностей (далее т.в.) понимается всякий факт, который в результате опыта может произойти или не произойти. Отношения между событиями бывают следующими:

А) два события называются несовместными в данном опыте, если никакие два из них не могут появиться вместе.

Б) события называются равновероятными, если по условиям симметрии есть основание считать, что никакое из событий не является объективно более возможным, чем другое.

В) событие называется благоприятствующим некоторому событию, если появления этого случая ведет за собой появление данного события.

2) Вероятность. Классическая форма определения вероятности. Геометрическая вероятность.

Вероятность – число, связанное с событием, которое чем больше, чем более возможно событие. Вероятность p лежит в интервале 0 ≤ P < 1. Классически вероятность определяется по формуле 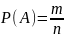, где m – число случаев, благоприятствующих событию А, n – общее число случаев. Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω.

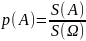
3) Частота случайного события и её свойства. Частотная интерпретация вероятности случайного события.

Частота события является статистической вероятностью события А и определяется по формуле , где m – число появлений события А, n – общее число произведенных опытов. Говорят, что величина X_n сходится по вероятности к величине а, если 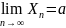. Это свойство частоты составляет содержание теоремы Бернулли.

4) Аксиоматическое построение теории вероятностей. Аксиомы т.в. и их следствия.

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем заранее неизвестно, какое именно. Случайные величины делятся на два больших класса: дискретные и непрерывные.

Практически невозможным событием называется событие, вероятность которого хотя и очень мала, но не равна нулю.

Практически достоверным событием называют событие, обратное практически невозможному.

Принцип практической уверенности: если вероятность некоторого события А в данном опыте Е весьма мала, то можно быть практически уверенным в том, что при однократном выполнении опыта Е событие А не произойдет.

5) Определение вероятности суммы случайных событий (далее с.с.) на множестве равновозможных с.с.

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из них. Вероятность суммы независимых событий равняется сумме их вероятностей, то есть P(A+B) = P(A) + P(B). Отсюда следует, что сумма вероятностей событий, образующих полную группу, равна единице, то есть 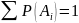. Противоположенными событиями называются два несовместных события, образующих полную группу. Сумма вероятностей противоположенных событий равна единице.

6) Зависимость событий и условная вероятность. Определение вероятности произведения с.с.

Произведением нескольких событий называется событие, состоящее в совместном появлении этих событий. Вероятность суммы независимых событий равняется сумме их вероятностей, то есть P(ABC) = P(A)*P(B)*P(C). Противоположенными событиями называются два несовместных события, образующих полную группу. Отсюда следует, что произведение противоположенных событий равно нулю.

Событие А называется независимым от события В, если вероятность события А не зависит, произошло ли событие В. Иначе называется зависимым. Вероятность события А, вычисленная при условии, что произошло событие В, называется условной вероятностью события А и обозначается Р(А|В). Отсюда формулировка независимости событий принимает следующий вид. Для несовместных событий Р(А) = Р(А|В).

Вероятность произведения двух событий считается по формуле Р(АB) = Р(A)*Р(А|В).

7) Формула полной вероятности и формула Байеса.

Формула полной вероятности: 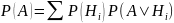, где H_i – гипотезы, вместе с которыми может произойти событие А. Гипотезы несовместны.

Формула Байеса. Условная вероятность гипотезы H_i при появлении события А:

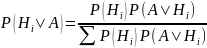
8) Частная теорема о повторении опытов.

Несколько опытов называются независимыми, если вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты.

Частная теорема о повторении опытов говорит о том, что при произведении n независимых опытов в одинаковых условиях (P(A)=const), то вероятность того, что событие A произойдет ровно m раз равно 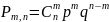, а распределение вероятностей такого вида называют биномиальным.

9) Общая теорема о повторении опытов.

Общая т.п.о. основывается на понятии производящей функции и высчитывается по формуле 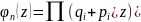, где z – произвольный параметр и говорит нам о том, что вероятность того, что событие А в n независимых опытах появится ровно m раз равна коэффициенту при z^m, то есть 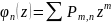. Очевидно, что при p_1=…= p_n получим производящую функцию , откуда следует формула частной т.п.о.

10) Случайные величины (далее с.в.). Закон распределения и его формы. Ряд и многоугольник распределения.

Случайная величина – величина, которая в результате опыта может принять то или иное значение, причем заранее неизвестно, какое именно.

Законом распределения с.в. называется всякое соотношение, устанавливающее связь между возможными значениями с.в. и соответствующими вероятностями. Таблица, ставящая каждому x_i в соответствие вероятность p_i, называется рядом распределения. При графическом изображении, когда по оси абсцисс откладывают возможные значения с.с., а по оси ординат вероятности этих значений, полученный рисунок называют многоугольником распределения. Ряд и многоугольник распределения полностью характеризуют случаную величину.

11) Функция распределения (ф.Р.) одномерной с.В. И её свойства.

Ф.Р. одномерной величины имеет вид F(x)=P(X < x), то есть вероятность того, что случайная величина X попадет на отрезок от 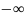до x. Отсюда очевидно следует, что ; 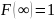. Ф.Р. является самой универсальной характеристикой с.в. Она существует для всех видов с.в.

Свойства: Вероятность попасть на интервал от α до β равна

P(α ≤ X < β) = F(β) - F(α), то есть вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке. Отсюда следует, что вероятность того, что непрерывная случайная величина примет определенное значение равна нулю.

12) Плотность вероятности (П.В.) одномерной с.в. и её свойства.

П.В. является производной от Ф.Р.: f(x) = F'(x). А значит, вероятность попасть на интервал от α до β равна P(α ≤ X < β) = F(β) - F(α) =

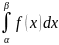
Свойства:

А) f(x)≥0

Б) P( ≤ X < ) =

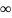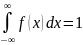
13) Числовые характеристики одномерных с.в.. Характеристики положения.

Числовая характеристика – характеристика, выражающая в сжатой форме наиболее существенные особенности распределения с.в..

Характеристики положения:

А) Матожидание случайной величины является суммой произведений всех возможных значений случайно величины на вероятности этих значений. 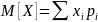- для дискретных величин. 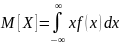для непрерывных величин. Модой с.в. называют её наиболее вероятное значение. Медиана делит график П.В. так, что

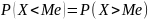
14) Моменты с.в.. Дисперсия и ско. Связь дисперсии, второго начального момента и матожидания.

Начальным моментом s-го порядка называется

А) Для дискретной с.в.

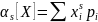
В) Для непрерывной с.в.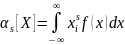

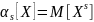
Центрированная с.в. называется отклонение с.в. X от его матожидания

X^o=X 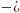m_x, отсюда очевидно, что

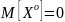
Центрированный начальный момент

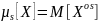
Второй центральный момент называется дисперсией и равен

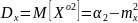
Ско

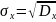
15) Закон равномерной плотности. Ф.Р., П.В., числовые хар-ки.

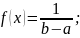
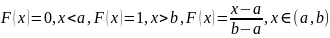
16) Биномиальный з.р.. Ф.Р., П.В., числовые хар-ки.

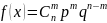
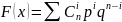
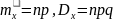
17) Закон Пуассона. Ф.Р., П.В., числовые хар-ки.

P_m = 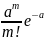– вероятность принять определенное значение m

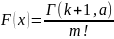
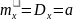
18) Предельные свойства биномиального з.р.

Если число испытаний n в схеме независимых испытаний растет, а вероятность p уменьшается, то точная формула практически непригодна из-за громоздких вычислений и возникающих погрешностей округления. В этом случае пользуются приближенными формулами Пуассона (на практике при npq < 10),

причем a = np

19) Нормальный з.р. Ф.Р., П.В., числовые хар-ки.

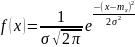
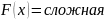
20) Определение вероятности попадания значения нормально распределенной величины в отрезок. Интеграл вероятностей и его свойства.

Интеграл вероятностей

F(x) =

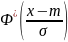
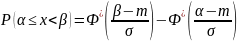
Свойства:

;

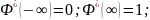
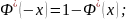
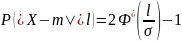21) Система с.в. Функция распределения 2-х с.в. и её свойства.

Функцией распределения системы двух с.в. (X,Y) называется вероятность совместного выполнения условий X<x, Y<y: F(x,y)=P((X<x)(Y<y)).

Свойства:

А) F(x,y) неубывающая функция обоих аргументов.

Б) Повсюду на F(x,y) = 0;

В) При одном из аргументов, равному 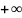, функция распределения от двух аргументов переходит в функцию от одного.

Г)

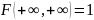
22) Система с.в. П.В 2-х с.в. и её свойства. Кривые равной плотности вероятности

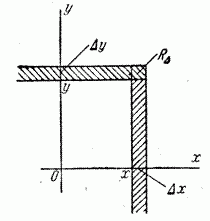
Вводя в рассмотрение плотность распределения для одной случайной величины, мы определяли ее как предел отношения вероятности попадания на малый участок к длине этого участка при ее неограниченном уменьшении. Аналогично определим плотность распределения системы двух величин.

П усть имеется система двух непрерывных случайных величин , которая интерпретируется  случайной точкой на плоскости . Рассмотрим на этой плоскости малый прямоугольник  со сторонами  и , примыкающий к точке с координатами Вероятность попадания в этот прямоугольник равна

Если пересечь поверхность распределения  плоскостью, параллельной плоскости , и спроектировать полученное сечение на плоскость , получится кривая, в каждой точке которой плотность распределения постоянна. Такие кривые называются кривыми равной плотности. Кривые равной плотности, очевидно, представляют собой горизонтали поверхности распределения. Часто бывает удобно задавать распределение семейством кривых равной плотности.

Свойства:

А) Плотность распределения системы есть функция неотрицательная:

Б) Двойной интеграл в бесконечных пределах от плотности распределения системы равен единице:                                                     

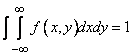
Это видно из того, что интеграл (8.3.6) есть не что иное, как вероятность попадания во всю плоскость , т.е. вероятность достоверного события.