15. Характеристические (вторичные) параметры пассивных четырехполюсников. Повторное сопротивление четырехполюсника.

В режиме работы симметричного четырехполюсника, входное сопротивление равно нагрузочному, т.е.

.

Это сопротивление обозначают  и называют характеристическим сопротивлением симметричного четырехполюсника, а режим работы четырехполюсника, для которого справедливо

,называется режимом согласованной нагрузки.

Для симметричного четырехполюсника ,

Характеристическим сопротивление можно записать как

,

решением которого является

С учетом такого решения, получим

;

.

,

где  - коэффициент распространения;  - коэффициент затухания (в неперах);  - коэффициент фазы (в радианах).

Одному неперу соответствует затухание по напряжению или току в е раз, а по мощности в е2  раз.

Характеристические параметры ищут с помощью сопротивления холостого хода и короткого замыкания.

Уравнения передачи четырехполюсника через характеристические параметры:

В условиях согласованного включения отношения напряжений (токов) четырехполюсника определяются только одним параметром.

  А_с - характеристическое ослабление, В_с - характеристическая фаза

  А_с - показывает ослабление полной мощности сигнала при передаче через согласованно включенный четырехполюсник.

Бел - единица измерения отношения двух мощностей.

В случае несимметричного четырехполюсника ( ) рассматривают два характеристических сопротивления и , где - входное сопротивление со стороны зажимов mn, когда нагрузка подключена к зажимам pq и равна :

- входное сопротивление со стороны зажимов pq, когда нагруз­ка , подключена к зажимам mn; при этом коэффици­енты А и D меняются местами:

Найдем решим совместно 2 предыдущих уравнения

Учитывая, что получим

Если четырехполюсник симметричен ( ), то , где равно входному сопротивлению четы­рехполюсника, когда он нагружен на .

Повторное сопро­тивление четырехполюсника - входное со­противление со стороны зажимов mn, если к выходным зажимам pq присоединено .

преобразовав уравнения заменив на , получим

Решив последнее уравнение относительно , найдем

Если четырехполюсник симметричный ( ), то т. е. оно совпадает с характеристическим сопротивлением Z_c.

16. Уравнение четырехполюсника в гиперболических функциях.

Для симметричного четырехполюсника А-форму уравнений записывают иногда через гиперболи­ческие функции от аргумента g, полагая , . При этом и

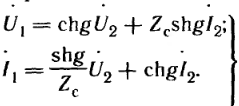
17. Соединения четырехполюсников, расчет с применением различных форм уравнений.

Форму записи уравнении применяют, исходя из соображений удобства. При нахождении связи между входными и выходными величи­нами различным образом соединенных четырехполюсников используют Z-, Н-, G-, Y- и А-формы

При последовательно-последовательном соединении четырехполюс­ников а и b применяют Z-форму:

при параллельно-параллель­ном соединении-Y-форму:

при последовательно-параллель­ном - H-форму:

при параллельно-последовательном - G-форму:

при каскадном - А -форму.

При параллельно-параллельном, последовательно-последова­тельном, параллельно-последовательном и последовательно-па­раллельном соединениях необходимо соблюдать условие регуляр­ности соединения четырехполюсников - через оба первичных зажима каждого четырехполюсника должны течь равные по значе­нию и противоположные по направлению токи; то же и по отноше­нию к вторичным зажимам.

При регулярном соединении матрица каждого четырехполюс­ника должна оставаться такой же, какой она была до соединения четырехполюсников. Регулярное соединение:

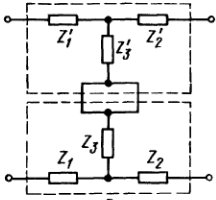
здесь перекрещены обе пары концов второго четырехполюс­ника (при перекрещивании обеих пар концов все элементы любой матрицы остаются неизменными).