42. Одномерные потоки несмешивающихся жидкостей. Плоскорадиальное вытеснение.
Одномерные потоки несмешивающихся жидкостей
Рассмотрим одномерные течения двух несмешивающихся жидкостей в недеформируемой однородной пористой среде.
Плоскорадиальное вытеснение
При закачке в пласт вытесняющей жидкости (фаза 1) через одиночную скважину из уравнений
, (4.127)
, (4.128)
,
,
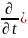(4.129)
,
, (4.130)
, , (4.133) для определения неизвестных функций получим:
,
,
,
,
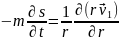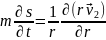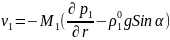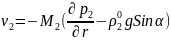(4.134)
Где
для удобства введена функция насыщенности
,
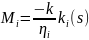(i=1,2)
(4.135)
r – текущее расстояние от центра скважины до произвольной точки пласта.
Окончательное
уравнение для насыщенности имеет вид:
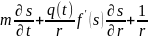
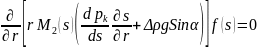(4.138),
q(t)=Q(t)/2
pi
h
При
q(t)
= q0=Const
уравнение (4.138) упрощается и если ввести
безразмерные параметры
,
,
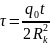(4.139)
где Rk расстояние от нагнетательной до добывающей скважины, то уравнение для насыщенности принимает вид
,
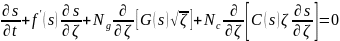(4.140) , здесь обозначено:
,
,
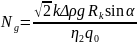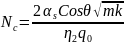G(s)=k2(s)f(s),
C(s)=G(s)J’(s), (4.141)
Уравнение (4.140) известно как уравнение Раппопорта-Лисса, описывает одномерные течения двух несжимаемых фаз. С точки зрения математики, это нелинейное уравнение параболического типа и описывает кроме простых течений фильтрации еще и нелинейные волны движущееся с постоянной скоростью.
43. Модель Маскерта – Миреса трехфазной фильтрации.
Изучение фильтрации трехфазных смесей имеет большое практической значение, т.к. в нефтегазоносных пластах при определенных условиях происходит совместное движение нефти, воды и свободного газа. Например, при движении нефти со свободной водой при достижении давления ниже давления насыщения газов в пласте образуется смесь (нефть+вода+газ). Система уравнений описывающих движение трехфазной смеси включает: закон фильтрации Дарси (для каждой фазы)
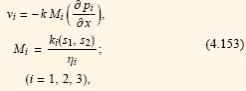
уравнения неразрывности фаз
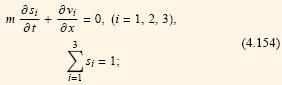
условия капилярного равновесия
В дальнейшем будем считать, что i = 1 соответствует наиболее смачиваемой фазе, i = 2 наименее смачиваемой фазе, i = 3 - промежуточной фазе. Кроме того считаем, что краевые углы смачивания в каждой точке течения одинаковые.
Тогда для системы "вода - нефть - газ" такой способ упорядочивания фаз будет зависеть от того, какой является пористая среда:
- гидрофильной (лучше смачиваемой водой)
- или гидрофобной (лучше смачиваемой нефтью).
В гидрофильной среде индексы (1,2,3) будут отвечать воде, газу, нефти. В гидрофобной среде - нефти, газу, воде. если исключить из системы (4.153)-(4.155) давление pi, то уравнения относительно искомых насыщенностей имеют вид
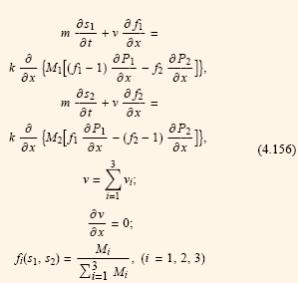
Функции fi(s1, s2) функции Бакли-Леверетта. Скорость фильтрации можно принять постоянной v = Const.