40.Модель Бакли-Леверетта.

Рассмотрим процесс вытеснения происходящим в прямолинейном тонком горизонтальном образце, представленном однородной и изотропной пористой средой (m, k = const).

В рассматриваемый образец, первоначально заполненный нефтью, а через сечение x = 0 закачивается вода. В процессе вытеснения образуется зона совместного движения воды и нефти. vw, vo скорости фильтрации соответственно воды и нефти,

Qw , Qo объемные расходы воды и нефти,

w, o коэффициенты динамической вязкости воды и нефти,

s sw водонасыщенность.

Kw(s),k0(s) – относит фазовые проницаемости

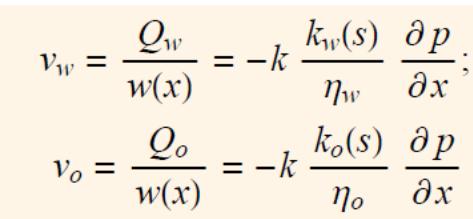
Для рассматриваемого двухфазного течения водо- и нефтенасыщенность sw, so - связаны очевидной зависимостью

Для описания движения воспользуемся следующими общими уравнениями: ур. Неразрывности:

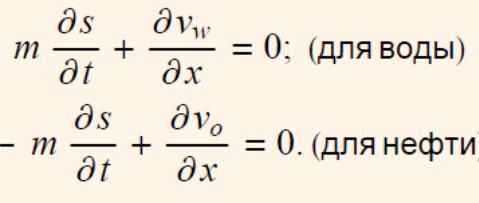
Поэтому сложив уравнения (4.111) найдем первый интеграл движения жидких фаз в виде

Равенства (4.112) показывают, что суммарная скорость v(t) двухфазного потока (а значит и расход фаз) не зависят от координаты x.

Из уравнения движения приведенного выше выводим следующее Равенство , , Если , то

F(s)- ф. бакли-леверетта. Она имеет простой физический смысл: это отношение скоростей -скорости вытеснения вытекающей жидкости к скорости вытесняющей.

Из (4.116) и (4.117) окончательно получаем уравнение Бакли-Леверетта

модельные решения уравнения Бакли-Леверетта в общих чертах правильно описывают процесс вытеснения нефти водой, а численнная реализация (в кодах среды Mathematica, н-р) позволяет строить и моделировать процессы вытеснения нефти и для конкретных, а не только модельных процессов.

Представленные численные решения и методы построения функции Бакли-Леверетта являются первым шагом в построении новых и адекватных математических моделей фильтрации многофазных

фильтрационных потоков.

41. Характеристики макроскопического описания многофазной фильтрации. Уравнения многофазной фильтрации.

Углеводородные системы могут быть гомо- и гетерогенными. В гомогенной системе все ее части имеют одинаковые физические и химические свойства. Для гетерогенной системы физические и химические свойства в разных точках различны. Гетерогенные системы состоят из фаз. Фаза - это часть системы, которая является гомогенной и отделена от других фаз отчетливыми границами.

Полагаем, что существует элементарный макрообъем ΔV, по которому производися усреднение.

Средняя приведенная плотность i - й фазы равна 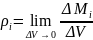, (i=1,2…n), (4.121)

Так что плотность смеси равна 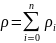(4.122)

Где 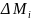масса i - й фазы в элементарном объеме 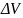, включая твердый скелет.

Основные характеристики многофазного течения:

- насыщенность s_i

- скорость фильтрации

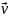
истинные плотности каждой фазы , как отношение массы i - й фазы в поровом объеме, занятого этой фазой. 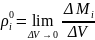, (i=1,2…n), (4.123), откуда с учетом (4.123) и определений насыщенности s_i и пористости m получаем соотношение 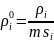, (4.124). Истинные плотности входят в термодинамические уравнения, например, в уравнения состояния. Скорость фильтрации 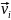связана с действительной скоростью 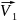соотношением 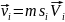, (4.125) .

Характерной особенностью многофазной фильтрации является влияние на процесс фильтрации поверхностного натяжения на границе раздела сред и возникновение на ней капиллярного скачка давления определяемого по формуле Лапласа 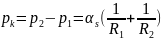, (4.126), где 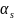- коэффициент межфазного натяжения R₁, R₂ – главные радиусы кривизны поверхности раздела фаз в данной точке, p_i – давление в каждой фазе, образующей связанную область и понимается как величина усредненная по элементарному макрообъему.

Для медленной совместной фильтрации можно предположить, что при данной насыщенности жидкости распределены так же, как и в условиях гидростатического равновесия. Это означает:

- разность давлений в двух фазах ( p₁- p₂) равна капиллярному давлению p_k - которое считается известной экспериментальной функцией насыщенности 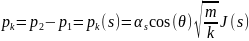, (4.127), где 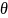- статический краевой угол смачивания между жидкостями и породой , 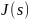- безразмерная функция Леверетта.

- гидравлические сопротивления и относительные проницаемости каждой из фаз являются однозначно определенными функциями насыщенности.

- закон движения каждой из фаз определяется обобщенным законом Дарси.

Таким образом, при описании многофазной фильтрации кроме v_i, p_i появляются новые - это насыщенности s_i.

Исходные уравнения многофазной фильтрации

Уравнение неразрывности

Уравнения неразрывности для каждой фазы имеет вид 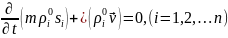, (4.128)

Обозначим s₁= s насыщенность более смачивающей фазы, а s₂ = (1–s) насыщенность другой 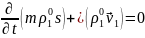, В случае, если вытесняемая и вытесняющая фазы - упругие жидкости, то влиянием сжимаемости на распределение насыщенности можно пренебречь.

Если жидкость и пористую среду принять несжимаемыми ,

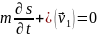Уравнения движения

Для каждой фазы в качестве уравнения движения, считаем справедливым обобщенный закон Дарси

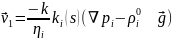, (i=1,2), (4.131), где k – абсолютная проницаемость пласта, 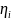- коэффициент динамической вязкости фаз, 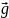- вектор ускорения свободно падения.

Связь между давлениями считается известной функцией насыщенности , (4.132)

Уравнения состояния

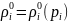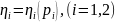, , (4.133)