30. Дифференциальные уравнения неустановившейся фильтрации упругой жидкости в упругой среде. Одномерные фильтрационные потоки. Основная ф-ла теории упругого режима.

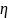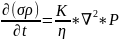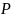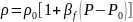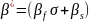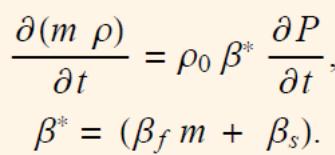Обратимся к общему дифференциальному ур-ию нестационарной фильтрации в изотропном грунте (2.15) неустановившегося движения сжимаемого флюида в деформированной пористой среде при k и = константе: (4.7), где - функция Лебензона. Уравнения состояния сред: упругой жидкости (4.8); упругой пористой среды (4.9); Из (4.8) и (4.9) находим: ; Выражение функции Лейбензона P для упругой жидкости: P=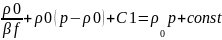 (4.11); Дифференциальное уравнение упругого режима: 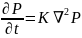(4.12),где K= 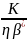(4.13), K – коэфф-т,который хар-ет скорость перераспределения пластового давления при неустановившейся фильтрации. (пьезопроводимости пласта)

Прямолинейно-параллельный поток упругой жидкости. а уравнение движения запишется в виде

Плоскорадиальный поток упругого флюида. Уравнение движения:

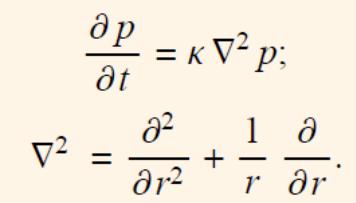
31. Фильтрация в деформированной упругой среде. Совместные уравнения фильтрации и деформированной среды.

Связанные процессы деформирования флюидонасыщенной пористой среды и фильтрации в линейной постановке могут быть описаны системой уравнений вида:

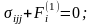
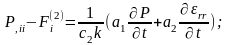
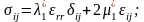
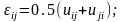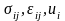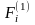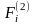(4.21) где -макронапряжения, макродеформации и макроперемещения системы "упругий скелет-флюид"; Р - давление флюида в порах, -объемная сила действующая на систему "упругий скелет-флюид", - объемная сила действующая на флюид; с₂-объемная концентрация пор; k - коэффициент фильтрации флюида, -эффективные постоянные системы "упругий скелет-флюид", которые определяются формулами:

де K₁, 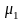-модули объемного сжатия и сдвига твердой фазы, K₂ - модуль объемного сжатия флюида.

Напряжения в твердой фазе связаны с макронапряжениями и поровым давлением флюида зависимостью:

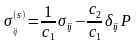(4.23) Так как прочность насыщенного пористого материала полностью зависит от прочности твердого скелета, то можно сделать вывод, что несущая способность среды зависит от пористости и давления во флюиде.

33. Дифференциальные уравнения неустановившейся фильтрации газа. Уравнение л.С. Лейбензона.

Для вывода дифференциального уравнения неустановившейся фильтрации совершенного газа воспользуемся уравнением:

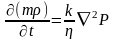(4.35)

где P - функция Лейбензона для совершенного газа определяется: 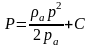; (4.36)

Из (4.35) и (4.36) окончательно выводим

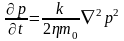
Полученное уравнение неустановившейся фильтрации называется уравнением Л.С. Лейбензона. Другой вид этого же уравнения представлен ниже 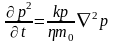C точки зрения расчетных методов - это нелинейное дифференциальное уравнение в частных производных параболического типа.

32. Напряженное состояние в окрестности сферической полости во флюидонасыщенном массиве. Тензор напряжений в твердом «скелете» пористой среды.

Рассмотрим полубесконечный тяжелый пористый массив, насыщенный флюидом. Ненарушенный массив находится в состоянии равновесия, которое характеризуется поровым давлением P₀ и макронапряжениями 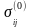. При этом в невозмущенном состоянии фильтрация отсутствует. После образования сферической выработки начального радиуса R₀ происходит перераспределение напряжений в окресности выработки и начнется фильтрация флюида.

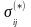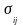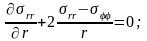= + ; P^*=P₀+P; (4.24) где _ij, P - дополнительные напряжения и давление вызванные наличием выработки. Задача для нахождения дополнительного состояния имеет вид: - уравнения равновения твердого "скелета" пористой среды (сферические координаты): r – радиус, фи – зенитный угол, тета-азимутал. угол

- уравнения движения флюида в твердом "скелете" имеет вид:

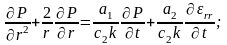
- уравнения состояния (закон Гука):

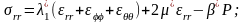
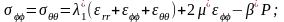
- уравнения Коши:

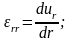
Тензор напряжений в твердом «скелете» пористой среды.

При радиальной деформации пористой среды и отсутствии смещений по другим направлениям, тензор макронапряжений напряжений имеет вид:

;

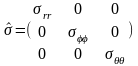Частное решение (4.30) соответствующее радиальной деформации имеет вид:

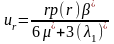
Напряжения в "скелете" пористой среды вычисляются следующим образом: