
- •25. Двумерная напорная фильтрация в скважине. Эксплуатационные скважины (эс). Дебит скважины (дс).
- •26. Формула Дюпюи. Формула Дюпюи для грунтов радиально переменной проницаемости.
- •27. Формула Дюпюи для грунтов с прерывно изменяющейся проницаемостью.
- •29. Упругий режим пласта и его особенности. Движение упругого флюида в упругой среде. Расчет упругого запаса жидкости в пласте.
- •30. Дифференциальные уравнения неустановившейся фильтрации упругой жидкости в упругой среде. Одномерные фильтрационные потоки. Основная ф-ла теории упругого режима.
- •31. Фильтрация в деформированной упругой среде. Совместные уравнения фильтрации и деформированной среды.
- •33. Дифференциальные уравнения неустановившейся фильтрации газа. Уравнение л.С. Лейбензона.
- •32. Напряженное состояние в окрестности сферической полости во флюидонасыщенном массиве. Тензор напряжений в твердом «скелете» пористой среды.
- •34. Особенности фильтрации на больших глубинах.
- •35. Линейное дифференциальное уравнение л.С. Лейбензона и его решение.
- •36. Точное решение линейной задачи о притоке газа к скважине с постоянным дебитом.
- •37. Прямолинейное вытеснение нефти.
- •38. Радиальое вытеснение нефти водой.
- •40.Модель Бакли-Леверетта.
- •41. Характеристики макроскопического описания многофазной фильтрации. Уравнения многофазной фильтрации.
- •42. Одномерные потоки несмешивающихся жидкостей. Плоскорадиальное вытеснение.
- •43. Модель Маскерта – Миреса трехфазной фильтрации.
26. Формула Дюпюи. Формула Дюпюи для грунтов радиально переменной проницаемости.
Рассмотрим
простой случай, когда скважина
эксплуатационная, центр расположен в
начале координат
 ,
тогда комплексный потенциал фильтрационного
течения: W=
,
тогда комплексный потенциал фильтрационного
течения: W=
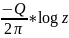 (3.22) будет описывать радиальный поток
жидкости к началу координат. Потенциал
скорости, который определяется с
точностью до произвольной постоянной
- С , в этом случае равен:
(3.22) будет описывать радиальный поток
жидкости к началу координат. Потенциал
скорости, который определяется с
точностью до произвольной постоянной
- С , в этом случае равен:
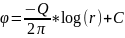 (3.23). Одно из окружностей радиуса
можно рассматривать в качестве границы
скважины
,
а другую внешнюю предыдущей радиуса
(3.23). Одно из окружностей радиуса
можно рассматривать в качестве границы
скважины
,
а другую внешнюю предыдущей радиуса
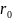 в качестве границы области питания
.
в качестве границы области питания
.
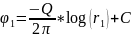 и
и
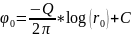 (3.24), Q=
(3.24), Q=
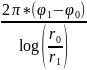 (3.25) определяет количество жидкости,
поступающее в скважину в единицу
времени, отнесенная к единице мощности
пласта, т.е. дебит скважины , и наз-ся
формулой Дюпюи.
(3.25) определяет количество жидкости,
поступающее в скважину в единицу
времени, отнесенная к единице мощности
пласта, т.е. дебит скважины , и наз-ся
формулой Дюпюи.
Пусть
грунт имеет постоянную проницаемость
k,
вязкость жидкости постоянная, жидкость
несжимаемая
и находится под действием силы тяжести.
Тогда имеем
![]()
![]()
Жидкость сжимаемая Пусть движение жидкости установившееся, а жидкость сжимаемая.
Давление
и плотность связаны соотношением
![]() ро0,
p0
соответственно давление и плотность
ро0,
p0
соответственно давление и плотность
на
границе области питания![]() .
.
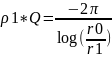 *
*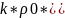
Формула
Дюпюи для грунтов радиально переменной
проницаемости: Пусть
коэфф проницаемости грунта зависит от
расстояния от начала координат: k=k(r)
(3.37) . Соответствующий потенциал для
несжимаемой и сжимаемой жидкости равен:
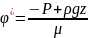 ;
;
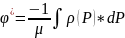 (3.38). Дебит скважины определяется: Q=2
(3.38). Дебит скважины определяется: Q=2 (3.39). Рассчитаем дебит скважин для
проницаемости: Q=
(3.39). Рассчитаем дебит скважин для
проницаемости: Q=
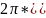 (3.40).
(3.40).
27. Формула Дюпюи для грунтов с прерывно изменяющейся проницаемостью.
Рассмотрим
работу круговой скважины радиуса
на границе которой известно
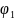 .
Пусть граница в области питания будет
концентрическая к
, окружность
на границе которой известно
.
Пусть граница в области питания будет
концентрическая к
, окружность
на границе которой известно
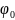 .
Пусть проницаемость грунта в кольце
будет меняться скачкообразно при r=
.
Пусть проницаемость грунта в кольце
будет меняться скачкообразно при r=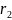 .
Тогда в области А определяемое неравенство
.
Тогда в области А определяемое неравенство
 ,
,
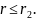 Проницаемость грунта =
Проницаемость грунта =
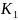 ,
и в области В определяемое неравенством
,
и в области В определяемое неравенством
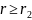 ;
;
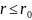 проницаемость =
проницаемость =
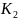 .
Течения будут радиальными и комплексные
потенциалы в областях А и В соответственно
равны:
.
Течения будут радиальными и комплексные
потенциалы в областях А и В соответственно
равны:
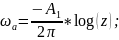
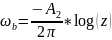 (3.42) , следовательно соответствующие
потенциалы фильтрационных течений
потенциалы будут равны:
(3.42) , следовательно соответствующие
потенциалы фильтрационных течений
потенциалы будут равны:
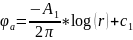 ;
;
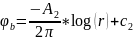 (3.43). 4 неизвестных:
(3.43). 4 неизвестных:
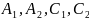 найдем на границе скважины, границе
области питания, и на границе раздела
двух сред. При r=
=>
найдем на границе скважины, границе
области питания, и на границе раздела
двух сред. При r=
=>
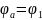 ; при r=
=>
; при r=
=>
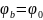 ; при r=
=>
; при r=
=>
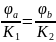 ;
;
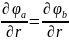 (3.44).
(3.44).
Из
условия (3.33): (для сжимаемой жидкости
формула дебита :
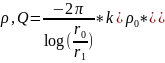 ) имеем 4 уравнения для определения
.
Следовательно , формула дебита: Q=
) имеем 4 уравнения для определения
.
Следовательно , формула дебита: Q=
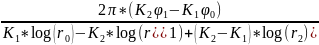 (3.45).
(3.45).
29. Упругий режим пласта и его особенности. Движение упругого флюида в упругой среде. Расчет упругого запаса жидкости в пласте.
Для появления упругих сил необходимо, чтобы фильтрационный поток был однофазным, т.е. давление в любой части потока должен быть выше давления насыщения жидкости газом. Характерная особенность проявления упругого режима в процессе разработки нефтяных месторождений это длительность процесса перераспределения пластового давления после начала работы скважины, или изменения темпа отбора из скважины.
Расчет
упругого запаса жидкости в пласте. Это
кол-во жидкости, которое можно извлечь
из пласта при понижении давления в нем
за счет объемной упругости пласта и
насыщающей его жидкости. Упругий запас
жидкости в пласте можно подсчитать
следующим образом: выделим элемент
объема
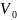 .
Пусть
.
Пусть
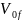 -объем жидкости в выделенном объеме, а
-объем жидкости в выделенном объеме, а
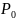 - начальное давление. Упругий запас
жидкости будем определять по ее объему,
замеряемому при начальном давлении.
Обозначим через
- начальное давление. Упругий запас
жидкости будем определять по ее объему,
замеряемому при начальном давлении.
Обозначим через
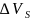 - изменение упругого запаса жидкости
внутри объема пласта
.
При изменении давления во всех его
точках на величину
- изменение упругого запаса жидкости
внутри объема пласта
.
При изменении давления во всех его
точках на величину
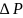 :
:
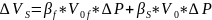 ( 4.1). Учтем, что начальный объем жидкости,
насыщающий элемент объема пласта
равен
полному объему пор в этом элементе:
( 4.1). Учтем, что начальный объем жидкости,
насыщающий элемент объема пласта
равен
полному объему пор в этом элементе:
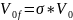 ,
где
,
где
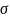 -
пористость (4.2).
-
пористость (4.2).
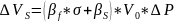 (4.3).
(4.3).
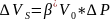 ,
,
 (4.4). Коэффициент
(4.4). Коэффициент
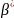 -
коэфф-т упругоемкости пласта. Из (4.4)
следует, что коэффициент
численно равен изменению упругого
запаса жидкости в единице объема пласта
при изменении пластового давления в
нем на единицу. Изменение упругого
запаса жидкости в пласте за время dt
равно объему отобранной жидкости: d
-
коэфф-т упругоемкости пласта. Из (4.4)
следует, что коэффициент
численно равен изменению упругого
запаса жидкости в единице объема пласта
при изменении пластового давления в
нем на единицу. Изменение упругого
запаса жидкости в пласте за время dt
равно объему отобранной жидкости: d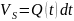 (4.5). Сравнивая ф-лы 4.4 и 4.5 , выводим
дифференциальное уравнение истощения
нефтяной залежи в условиях замкнутого
кругового режима:
(4.5). Сравнивая ф-лы 4.4 и 4.5 , выводим
дифференциальное уравнение истощения
нефтяной залежи в условиях замкнутого
кругового режима:
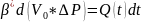 (4.6).
(4.6).
