25. Двумерная напорная фильтрация в скважине. Эксплуатационные скважины (эс). Дебит скважины (дс).

Скважина предназначена для отбора углеводородного сырья из пласта наз-ся эксплуатационной. Скважины, созданные для нагнетания внутри жидкости или газа наз-ся нагнетательными. Скважины бурятся также для того, чтобы определить основные хар-ки грунтов, насыщенных жидкостью. В частности, т.к. жидкость находится в пластах, то выясняется вопрос их толщин, которые называются мощностью пласта. Если скважина пронизывает всю толщу пласта, то она наз-ся совершенной. Фильтрация совершенных скважин представляет собой двумерное течение. Приток жидкости к скважине вызывается разностью давлений на границе скважин и на границе области питания, такая фильтрация наз-ся напорной. Границей области питания может быть пов-сть, вдоль которой пласт соприкасается со свободной жидкостью. Количество жидкости, протекающее к совершенной скважине в единицу времени, отнесенная к мощности пласта, наз-ся дебитом.

Рассмотрим плоскую напорную фильтрацию к совершенной скважине. Такие фильтрационные течения описываются комплексным потенциалом, который определяется по следующим граничным условиям: на заданной замкнутой границе скважины и по заданной границе области питания 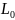задается давление. Т.к. последнее связано с потенциалом скорости соотношением: * ( (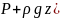3.19), и пласт горизонтальный , то : на , 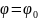на (3.20). В силу того, что на границе скважины в плане будет окружность и вдоль нее расход жидкости отличен от нуля, то в центре скважины искомый комплексный потенциал должен иметь член вида: 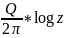. Т.к. граница должна быть окружностью и вдоль нее должно быть постоянно комплексный потенциал, описывающий течение к скважине запишем:

W= 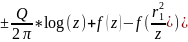(3.21). Знак + соотв-ет нагнетательной скважине, знак - соотв-ет эксплуатационной скважине. Начало координат выбрано в центре круглой скважины 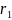ее радиус, Q - постоянная, f- аналитическая функция от z. Т.к. подбор функции 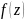такой, чтобы удовлетворялось бы второе условие формулы: затруднительно, то можно ставить обратную задачу, заключающуюся в том, что можно рассматривать различные варианты функции и определить кривые , вдоль которых 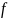сохраняет постоянное значение, или искать границу области питания.

№28. Приток флюида к группе случайно расположенных скважин.

Пусть в неограниченном горизонтальном пласте постоянной толщины h имеется группа добывающих и нагнетательных скважин нулевого радиуса (точечный сток или источник). Начальное пластовое давление во всем пласте (потоке) одинаково и равно P₀. Рассмотрим фильтрационное течение в окрестности группы скважин случайным образом расположенных на плоскости. Обозначим через Qi - дебит i-й скважины, а через c_i -комплексные координаты центров i-й скважины. Тогда согласно методу наложения решений комплексный потенциал течения: . Координаты c_i и дебиты Q_i задаем с помощью генератора случайных чисел. Координаты скважины на месторождении . 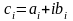Стационарное поле скоростей течения вычисляем как первую производную от комплексного потенциала по комплексной переменной z.