
- •5.3. Математические основы теории помехоустойчивого кодирования
- •5.3.1. Краткие сведения из теории чисел
- •4. Если и , то .
- •5.3.4. Векторное пространство
- •5.4.2. Параметры линейного кода
- •5.4.4. Циклические коды и корни полиномов
- •1. Порождающий полином неприводим и примитивен, а длина кода . Коды таких длин называют примитивными независимо от вида порождающего полинома.
- •5.4.5. Спектральное описание циклических кодов
- •5.5.2. Принципы декодирования кодов бчх
- •5.5.3. Методы реализации этапов декодирования кодов бчх
- •5.6.2. Обнаружение и исправление пакетов ошибок
- •5.7.3. Связь между блочными кодами
5.3. Математические основы теории помехоустойчивого кодирования
Основой построения наиболее важных из известных кодов является их алгебраическая структура, которая облегчает изучение различных свойств кода, а также обеспечивает возможность практической реализации кодирующих и декодирующих устройств.
В данном разделе излагаются основные понятия алгебры, необходимые для изучения теории помехоустойчивых кодов. Основные теоремы приводятся без доказательств. Заинтересованный читатель найдет их в [25, 26, 30, 33].
Важнейшими
объектами изучения в алгебре являются
алгебраические системы, т.е. множества,
в которых определены одна или несколько
операций, таких, например, как сложение
или умножение. Под операцией в общем
случае подразумевается однозначная
функция двух переменных, которая может
быть записана в виде ![]() ,
где
,
где ![]() –
знак операции. Примерами алгебраических
систем являются группы, кольца, поля и
др. Их свойства рассматриваются в
настоящем разделе.
–
знак операции. Примерами алгебраических
систем являются группы, кольца, поля и
др. Их свойства рассматриваются в
настоящем разделе.
5.3.1. Краткие сведения из теории чисел
Если ![]() ,
, ![]() и
и ![]() –
целые числа и
–
целые числа и ![]() ,
то говорят, что
,
то говорят, что ![]() делится
на
или
что
является
делителем
.
Наибольшим общим делителем (НОД) двух
чисел называется наибольшее целое
положительное число, являющееся делителем
обоих этих чисел. Говорят, что два числа
взаимно просты, если их НОД равен 1. Для
любой пары целых чисел
и
существует
единственная пара чисел
делится
на
или
что
является
делителем
.
Наибольшим общим делителем (НОД) двух
чисел называется наибольшее целое
положительное число, являющееся делителем
обоих этих чисел. Говорят, что два числа
взаимно просты, если их НОД равен 1. Для
любой пары целых чисел
и
существует
единственная пара чисел ![]() (частное)
и
(частное)
и ![]() (остаток),
таких, что
(остаток),
таких, что ![]() ,
где
,
где ![]() .
.
Если
два числа
и
дают
при делении на число ![]() один
и тот же остаток, то говорят, что
числа
и
сравнимы
по модулю
.
Сравнение записывается в виде
один
и тот же остаток, то говорят, что
числа
и
сравнимы
по модулю
.
Сравнение записывается в виде ![]() .
Эквивалентным определением сравнимости
двух чисел является делимость их разности
на
.
.
Эквивалентным определением сравнимости
двух чисел является делимость их разности
на
.
Отметим основные свойства сравнений.
1.
Если ![]() и
и ![]() ,
то
.
,
то
.
2.
Над сравнениями можно производить
операции, аналогичные операциям над
равенствами, т.е., если ![]() и
и ![]() ,
то
,
то ![]() ,
, ![]() и
и ![]() ,
где
,
где ![]() –
произвольное целое число.
–
произвольное целое число.
3.
Обе части сравнения и их модуль можно
разделить на их общий делитель, т.е.,
если ![]() ,
, ![]() и
и ![]() ,
то из
следует
,
то из
следует ![]() .
.
4.
Два числа, сравнимые по модулю
,
сравнимы и по модулю ![]() ,
если
–
любой делитель
.
,
если
–
любой делитель
.
Все
числа, сравнимые по модулю
,
образуют класс вычетов по модулю
.
Любое число в классе называется вычетом
по модулю
.
Всем числам класса вычетов соответствует
один и тот же остаток. Так как всего
имеется
остатков: ![]() ,
то существует
различных
классов вычетов. Вычет, равный самому
остатку, называется наименьшим
неотрицательным вычетом. Выбрав из
каждого класса вычетов по модулю
по
одному вычету, получим полную систему
вычетов по модулю
.
Обычно в качестве полной системы вычетов
используют наименьшие неотрицательные
вычеты:
.
,
то существует
различных
классов вычетов. Вычет, равный самому
остатку, называется наименьшим
неотрицательным вычетом. Выбрав из
каждого класса вычетов по модулю
по
одному вычету, получим полную систему
вычетов по модулю
.
Обычно в качестве полной системы вычетов
используют наименьшие неотрицательные
вычеты:
.
Пример
5.1. Пусть ![]() ,
тогда числа
,
тогда числа ![]() и
т.д. образуют класс вычетов по модулю
4. Наименьший вычет в этом классе равен
и
т.д. образуют класс вычетов по модулю
4. Наименьший вычет в этом классе равен ![]() ,
а полную систему вычетов по модулю 4
образуют числа
,
а полную систему вычетов по модулю 4
образуют числа ![]() .
.
С учетом определенного выше понятия сравнения чисел по модулю введены операции сложения и умножения чисел по модулю произвольного целого числа .
При
этом результат применения операции
сложения (умножения) двух чисел по
модулю
равен
наименьшему вычету класса, к которому
принадлежит число, получаемое в результате
обычного сложения (умножения) чисел.
Другими словами, результат применения
операции сложения (умножения) чисел по
модулю ![]() равен
остатку от деления числа, получаемого
при обычном сложении (умножении) чисел,
на модуль
.
равен
остатку от деления числа, получаемого
при обычном сложении (умножении) чисел,
на модуль
.
Пример
5.2. При ![]() таблицы
сложения и умножения чисел по модулю 5
выглядят следующим образом:
таблицы
сложения и умножения чисел по модулю 5
выглядят следующим образом:


5.3.2. Группы
Определение группы
Группой ![]() называется
множество элементов, для которых
определена некоторая операция
и
выполняются следующие аксиомы:
называется
множество элементов, для которых
определена некоторая операция
и
выполняются следующие аксиомы:
G.1. Операция может быть применена к любым двум элементам группы, в результате чего получается третий элемент группы, т.е., если
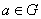 и
и 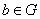 ,
то
,
то  .
.G.2. Для любых трех элементов , и из
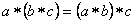 .
.G.3. В существует единичный элемент , т.е. такой, что
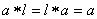 для
любого
.
для
любого
.G.4. Для любого элемента существует обратный элемент
 такой,
что
такой,
что 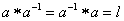 .
.
Аксиома
G.1 определяет замкнутость операции в
группе. Обычно операции над элементами
записывают в виде ![]() и
называют сложением или в виде
и
называют сложением или в виде ![]() и
называют умножением, даже если они не
являются обычными сложением и умножением.
В соответствии с двумя записями операций
различают аддитивную и мультипликативную
группы.
и
называют умножением, даже если они не
являются обычными сложением и умножением.
В соответствии с двумя записями операций
различают аддитивную и мультипликативную
группы.
Свойство операции, сформулированное в виде аксиомы G.2, называют ассоциативностью. Она означает, что порядок выполнения операций несущественен, и поэтому скобки не нужны.
Аксиома
G.3 постулирует обязательное существование
единичного элемента. Для аддитивной
группы единичный элемент называют
нулем, обозначают 0 и определяют из
уравнения ![]() .
Для мультипликативной группы единичный
элемент называют единицей и определяют
из уравнения
.
Для мультипликативной группы единичный
элемент называют единицей и определяют
из уравнения ![]() .
.
Аксиома
G.4 требует для каждого элемента группы
существования обратного элемента. Если
групповая операция – сложение, то
элемент, обратный
,
обозначается ![]() и
находится из уравнения
и
находится из уравнения ![]() .
Для мультипликативной группы обратный
к
элемент
обозначается
и
находится из уравнения
.
Для мультипликативной группы обратный
к
элемент
обозначается
и
находится из уравнения ![]() .
.
Группа называется коммутативной или абелевой, если кроме аксиом G.1 – G.5 выполняется следующая аксиома коммутативности.
G.5.
Для двух произвольных
элементов
и
из
справедливо ![]() .
.
Примеры групп
Пример
5.3. Одна из простейших аддитивных групп
состоит из двух элементов, одним из
которых является единичный элемент 0.
Второй элемент обозначим через
.
В соответствии с G.4 должен существовать
обратный элемент, такой, что ![]() .
Значит,
.
Значит, ![]() ,
и правило сложения записывается в
виде:
,
и правило сложения записывается в
виде: ![]() ;
; ![]() ;
; ![]() .
При
.
При ![]() имеем
правило сложения по модулю
имеем
правило сложения по модулю ![]() .
.
Пример 5.4. Совокупность всех действительных чисел образует группу относительно операции обычного сложения. Единичным элементом группы (нулем) является число 0.
Пример
5.5. Совокупность
всех действительных чисел без нуля
образует мультипликативную группу.
Единичным элементом при этом является
1, а обратным – число ![]() .
.
Пример
5.6. Совокупность
двоичных ![]() -символьных
комбинаций образует группу из
-символьных
комбинаций образует группу из ![]() элементов,
если в качестве групповой операции
используется посимвольное сложение по
модулю 2. Так, если
элементов,
если в качестве групповой операции
используется посимвольное сложение по
модулю 2. Так, если ![]() ,
, ![]() ,
то
,
то ![]() .
Единичным является элемент
.
Единичным является элемент ![]() ,
а обратный элемент равен самому элементу,
т.к.
,
а обратный элемент равен самому элементу,
т.к. ![]() .
.
Пример
5.7. Полная система вычетов по модулю
6 ![]() является
группой с операцией сложения по модулю
6. Единичным элементом этой группы
является 0, а обратный элемент находится
из равенства
является
группой с операцией сложения по модулю
6. Единичным элементом этой группы
является 0, а обратный элемент находится
из равенства ![]() .
Так, если
.
Так, если ![]() ,
то
,
то ![]() и
т.д.
и
т.д.
Все рассмотренные в примерах группы являются абелевыми.
Теорема 5.1. Группа содержит один единичный элемент, и каждый элемент группы имеет единственный обратный элемент.
Легко видеть, что в примерах 1 – 5 утверждения теоремы выполняются.
Число элементов в группе называется порядком группы. Если порядок конечен, группа называется конечной, в противном случае – бесконечной группой. В примерах 1.3, 1.6 и 1.7 рассмотрены конечные группы 2-го, -го и 6-го порядков, а в примерах 1.4 и 1.5 – бесконечные группы.
Подгруппы
Подмножество элементов группы называется подгруппой , если оно удовлетворяет всем аксиомам группы. Для того чтобы определить, является ли подгруппой , надо проверить только замкнутость операции и наличие обратных элементов. Подгруппами группы, рассмотренной в примере 2, являются множества: целых чисел, чисел, делящихся на 3, и т. д.
Смежные классы
Пусть
задана конечная группа ![]() содержащая
подгруппу
содержащая
подгруппу ![]() .
Табл. 5.1 составлена следующим образом.
Первая строка состоит из элементов
подгруппы: она начинается с единичного
элемента
,
и каждый элемент подгруппы появляется
в строке только один раз. Первым элементом
второй строки может быть любой элемент
группы, не вошедший в первую строку, а
все остальные элементы получаются путем
применения групповой операции
.
Табл. 5.1 составлена следующим образом.
Первая строка состоит из элементов
подгруппы: она начинается с единичного
элемента
,
и каждый элемент подгруппы появляется
в строке только один раз. Первым элементом
второй строки может быть любой элемент
группы, не вошедший в первую строку, а
все остальные элементы получаются путем
применения групповой операции ![]() .
Аналогично образуются третья, четвертая
и т.д. строки, каждая с неиспользованным
прежде элементом группы в начале строки,
до тех пор, пока каждый элемент группы
не войдет в таблицу.
.
Аналогично образуются третья, четвертая
и т.д. строки, каждая с неиспользованным
прежде элементом группы в начале строки,
до тех пор, пока каждый элемент группы
не войдет в таблицу.
Таблица 5.1 Разложение группы на смежные классы
|
|
|
∙∙∙ |
|
|
|
|
∙∙∙ |
|
|
|
|
∙∙∙ |
|
∙∙∙ |
∙∙∙ |
∙∙∙ |
∙∙∙ |
∙∙∙ |
|
|
|
∙∙∙ |
|
Полученная таблица задает разложение группы на смежные классы. Совокупность элементов в каждой строке называется левым смежным классом, а элемент в первом столбце строки называется образующим смежного класса.
Число
смежных (т.е. неперекрывающихся)
классов ![]() в
разложении группы по подгруппе называется
индексом
в
.
в
разложении группы по подгруппе называется
индексом
в
.
Правые
смежные классы получаются, если для
нахождения элементов строк применить
операцию ![]() .
Для коммутативной группы левый и правый
смежные классы совпадают.
.
Для коммутативной группы левый и правый
смежные классы совпадают.
Отметим основные свойства смежных классов.
1. Смежные классы не имеют общих элементов. Если у двух смежных классов оказался общий элемент, то такие смежные классы совпадают.
2. Левый (правый) смежный класс содержит столько элементов, каков порядок группы .
3.
Порядок
конечной
группы
есть
произведение порядка ![]() подгруппы
на
ее индекс
в
группе
(на
число смежных классов).
подгруппы
на
ее индекс
в
группе
(на
число смежных классов).
Группу можно рассматривать как объединение неперекрывающихся смежных классов.
Циклические группы
Пусть
–
один из элементов конечной группы
порядка
.
Обозначим элементы ![]() через
через ![]() (при
использовании операции сложения элементы
можно обозначать также
(при
использовании операции сложения элементы
можно обозначать также ![]() )
и рассмотрим последовательность
элементов
Так
как группа
конечна,
то существуют такие числа
)
и рассмотрим последовательность
элементов
Так
как группа
конечна,
то существуют такие числа ![]() и
и ![]() ,
что
,
что ![]() Но
тогда
Но
тогда ![]() и
и ![]() (единичный
элемент группы). Минимальное целое
положительное число
такое,
что
(единичный
элемент группы). Минимальное целое
положительное число
такое,
что ![]() ,
называют порядком элемента
.
,
называют порядком элемента
.
Очевидно,
если
–
порядок элемента
,
то все
элементов ![]() различны.
Доказано, что множество элементов
различны.
Доказано, что множество элементов ![]() является
подгруппой группы
.
Такая подгруппа называется циклической
подгруппой, порожденной элементом
.
является
подгруппой группы
.
Такая подгруппа называется циклической
подгруппой, порожденной элементом
.
Если
в группе
существует
элемент
такой,
что его порядок совпадает с порядком
группы ![]() ,
т.е.
,
т.е. ![]() ,
то сама группа называется циклической.
При этом элемент
называется
порождающим элементом группы.
,
то сама группа называется циклической.
При этом элемент
называется
порождающим элементом группы.
Теорема
5.2. Если
–
порождающий элемент циклической группы
порядка
,
то ![]() –
порождающий элемент этой же группы,
где
–
число взаимно простое с
.
–
порождающий элемент этой же группы,
где
–
число взаимно простое с
.
В примере 1.7 рассмотрена аддитивная циклическая группа 6-го порядка. Порождающими элементами этой группы являются 1 или 5. Циклическая группа с порождающим элементом приведена в примере 1.3.
5.3.3. Кольца и поля
Определение кольца
Кольцом ![]() называется
множество элементов, на котором определены
две операции – сложение и умножение, и
в
выполняются
следующие аксиомы:
называется
множество элементов, на котором определены
две операции – сложение и умножение, и
в
выполняются
следующие аксиомы:
R.1. Множество является аддитивной абелевой группой.
R.2. Для любых двух элементов и из определено их произведение:
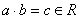 (замкнутость
операции умножения).
(замкнутость
операции умножения).R.3. Для любых трех элементов , и из выполняется ассоциативный закон, т.е.
 и
и 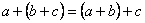 .
.R.4. Для любых трех элементов , и из выполняется дистрибутивный закон, т.е. справедливы равенства:
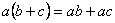 и
и 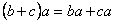 .
.
Заметим, что в кольце для операции умножения аксиомы G.3, G.4 и G.5 могут не выполняться. Если же операция умножения коммутативна в кольце, то такое кольцо называется коммутативным. Если в кольце существует единичный элемент относительно операции умножения (выполняется аксиома G.3), то это кольцо называется кольцом с единицей.
Пример 5.8. Все целые положительные и отрицательные числа и нуль образуют коммутативное кольцо с единицей относительно обычных операций сложения и умножения.
Пример 5.9. Легко убедиться, что полная система вычетов по модулю также образует коммутативное кольцо с единицей относительно операций сложения и умножения по модулю .
Определение поля
Полем ![]() называют
коммутативное кольцо с единицей, в
котором каждый ненулевой элемент имеет
мультипликативный обратный элемент
(т.е. обратный по умножению).
называют
коммутативное кольцо с единицей, в
котором каждый ненулевой элемент имеет
мультипликативный обратный элемент
(т.е. обратный по умножению).
Другими словами, полем называют множество, которое является аддитивной абелевой группой; ненулевые же элементы этого множества образуют мультипликативную абелевую группу, и выполняется закон дистрибутивности.
По аналогии с группами число элементов поля называется порядком поля. Поля, порядки которых конечны, называются конечными полями. Конечные поля имеют наибольшее значение в теории кодирования.
Отметим некоторые свойства полей, вытекающие из их определения.
1.
Для любого элемента поля ![]() .
.
2.
Для ненулевых элементов
и
поля ![]() .
.
3.
Для любых элементов
и
поля ![]() .
.
