5 Граф Шлефли

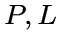• Обобщенным четырехугольником   называется конечная геометрия с множествами точек и прямых   и отношением инцидентности   таким, что каждая точка инцидентна точно 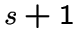  прямой, а каждая прямая инцидентна 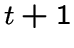  точке. При этом выполнены следующие аксиомы:

1. Две точки инцидентны не более одной прямой.

2. Две прямые инцидентны не более одной точке. Если две прямые инцидентны одной точке, то говорят, что эти прямые пересекаются.

3. Для любой прямой   и для любой не лежащей на ней точки   существует только одна прямая  , инцидентная   и пересекающая прямую  .

• Графом инцидентностей обобщенного четырехугольника   называется граф, множеством вершин которого является множество точек  , и две вершины смежны тогда и только тогда, когда точки лежат на одной прямой.

• Граф Шлефли -- это сильно регулярный граф с параметрами  , который является дополнительным к графу инцидентностей обобщенного четырехугольника  .

Известно, что граф инцидентностей обобщенного четырехугольника является сильно регуляреным графом. Обобщенный четырехугольник   существует и притом только один (см. теорему 1.15.2 и пример (iii) на стр. 30 монографии [6]).

Заметим, что если   граф Шлефли, то он является локально  -графом, где   -- граф Клебша. Более того, поскольку в   через любую точку   проходит 5 прямых, на каждой из которых по две точки, отличные от точки  , то любая антиокрестность в графе Шлефли изоморфна графу  . Таким образом любой подграф из   изоморфен  .

В следующем пункте приводится другое определение графа Шлефли.

6 Граф системы корней

• Дискретное множество векторо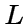в   в   замкнутое относительно сложения и вычитания векторов называется целой решеткой, если скалярное произведение любых двух векторов из   является целым числом.

• Целая решетка называется четной, если она состоит только из векторов четной нормы, то есть скалярное произведение 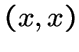  является четным числом для всех 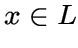 . Заметим, что целая решетка является четной, когда она имеет базис, состоящий из векторов четной нормы.

• Корневой решеткой называется целая решетка в  , порожденная векторами нормы 2.

Подмножество векторов данной корневой решетки   образуют систему корней   в  , то есть   является конечным множеством ненулевых векторов, порождающих  , таких, что выполнены следующие три условия:

            Граф – множество V вершин и набор Е неупорядоченных или упорядоченных пар вершин; обозначается граф через G(V, E). Неупорядоченная пара вершин называется ребром, упорядоченная пара –дугой. Граф, содержащий только ребра, называется неориентированным. Граф, содержащий только дуги, – ориентированным. Пара вершин может соединяться двумя или более ребрами (дугами одного направления), такие ребра (дуги) называются кратными. Дуга (или ребро) может начинаться и кончаться в одной и той же вершине, такая дуга (ребро) называется петлей.

            Далее под графом будем понимать граф без петель и кратных ребер; граф, в котором допускаются кратные ребра, назовем мультиграфом; а граф, в котором допускаются кратные ребра и петли –псевдографом.

            Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. Две вершины соединяются непрерывной линией тогда и только тогда, когда в графе Gесть ребро с этими вершинами. Ребра графа будем обозначать парами точек, например,  , а также малыми латинскими буквами (см. рис.1)

1

2

3

5

А

В

С

а

4

2

3

1

б)

в)

а)

Рис. 1

Вершины, соединенные ребром или дугой, называются смежными. Ребра, имеющие общую вершину, также называются смежными. Ребро (дуга) и любая из его двух вершин называются инцидентными. Говорят, что ребро   соединяет вершины А и В, а дуга   начинается в вершине А и кончается в вершине В. Вершина, не принадлежащая ни одному ребру, называется изолированной. Граф, состоящий только из изолированных вершин, называется нуль-графом. Граф называется полным, если любые две его различные вершины  соединены  одним  и  только одним ребром (рис.1, в)).

            Любой неполный граф можно дополнить до полного (рис. 2.)

3

1

2

4

3

1

2

4

а)

б)

Рис. 2

G

            Дополнением графа   называется граф   с теми же вершинами, что и граф  , и с теми и только теми ребрами, которые нужно добавить к графу  , чтобы он стал полным (рис.2, б)).

Пример 3.1. Выяснить, сколько ребер в полном графе с 5 вершинами.

Решение.

Изобразим полный граф с 5 вершинами (рис. 3).

1

2

3

4

5

Рис. 3

В данном графе  10 ребер: (1, 2),  (1, 3),  (1, 4),  (1, 5),  (2, 3), (2, 4), (2, 5), (3, 4), (3, 5),    (4, 5).

Число ребер графа, которым принадлежит вершина А, будем обозначать   и называть степенью вершины А. Вершина А называется четной, если   - четное число, и нечетной, если   - нечетное число.

Теорема 3.1. В графе сумма степеней всех его вершин есть число четное, равное удвоенному числу ребер графа.

                        Следствие. Число нечетных вершин графа четно.

Теорема 3.2. Во всем графе с n вершинами, где  , всегда найдутся по крайней мере две вершины с одинаковыми степенями.

Теорема 3.3. Если в графе с n вершинами, где  , в точности две вершины имеют одинаковую степень, то в этом графе всегда найдется либо в точности одна вершина степени 0, либо в точности одна вершина степени  .

Граф называется однородным степени n, если степень любой его вершины равна n.

Пример 3.2. Существует ли полный граф с 7 ребрами?

Решение.

Пусть у графа G имеется n вершин. Тогда степень каждой вершины равна   (т.к. граф полный). По условию в графе 7 ребер. По теореме 4.1. сумма степеней всех вершин равна  . С другой стороны, сумма степеней всех вершин графа равна  . Тогда получаем уравнение:  . Отсюда  . Решая его, получим  ,  ,  , отсюда следует, что полного графа с 7 ребрами не существует.

Пример 3.3. 7 студентов, разъезжаясь на каникулы, договорились, что каждый из них пошлет письма трем остальным. Может ли оказаться, что каждый получит письма от тех друзей, которым пишет сам?

Решение.

            Имеем граф с 7 вершинами, степень которых равна 3. Получаем следующую математическую интерпретацию данной задачи: существует ли неполный однородный граф с 7 вершинами степени 3? Сумма степеней вершин данного графа равна   - нечетное число. Получаем противоречие теореме 4.1, которая утверждает, что сумма степеней вершин графа есть число четное.

            Ответ:  не может.

ЧИСЛА РАМСЕЯ определяются как наименьшее значение п, для которого в любой группе из п точек либо некоторая группа из / точек образует полную сеть красных ребер, либо некоторая группа из * точек образует полную сеть синих ребер. Рисунки показывают, как велико должно быть конкретное число Рамсея. На первой диаграмме изображены пять точек, соединенные красными и синими ребрами таким способом, что никакие три точки не образуют ни красной, ни синей полной сети. Следовательно, из первой диаграммы можно вывести, что число Рамсея для трех красных и трех синих больше пяти. Аналогично можно утверждать, что из второй диаграммы следует, что число Рамсея для трех красных и четырех синих больше восьми. Другими более сложными методами можно показать, что число Рамсея для трех красных и трех синих равно шести, а число Рамсея для трех красных и четырех синих равно девяти. Все точно известные числа Рамсея приведены выше, кроме числа Рамсея для четырех красных и четырех синих, диаграмма для которого изображена на предыдущей странице. (На некоторых диаграммах синие ребра для простоты не показаны.) Относительно числа Рамсея для трех красных и восьми синих было доказано, что оно больше 27 и меньше или равно 29. Недавно было показано (но пока не подтверждено), что оно равно 28.