2 Регулярные графы

• Граф   называется регулярным валентности  , если любой подграф из множества   содержит   вершин для некоторого фиксированного  .

• Граф   называется реберно регулярным с параметрами  , если   -- регулярный граф на   вершинах валентности  , в котором каждый подграф из множества   имеет   вершин для некоторого фиксированного  .

• Граф   называется кореберно регулярным с параметрами  , если   является регулярным графом валентности  , в котором любая пара несмежных вершин имеет одно и то же число   вершин, смежных с ними обеими. Другими словами,   --  -регулярный граф диаметра два с соответствующими параметрами или   -- объединение непересекающихся полных графов с числом вершин  .

• Граф   называется сильно регулярным с параметрами 

если   -- реберно-регулярный и кореберно-регулярный граф с соответствующими параметрами.

• Граф   называется  -регулярным с параметрами 

если   -- регулярный граф на   вершинах валентности  , в котором каждый подграф из множества   имеет  вершин для некоторого фиксированного  .

• Граф   называется вполне регулярным с параметрами 

если   -- реберно-регулярный и  -регулярный граф с соответствующими параметрами.

• Пусть   -- регулярный граф валентности   и диаметра  . Граф   называется дистанционно регулярным с массивом пересечений 

если для каждого   параметры 

не зависят от выбора пары вершин   из   такой, что  .

3 Расширения графов

• Пусть 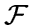  -- класс графов. Граф   называется локально  -графом, если любой подграф   из   изоморфен некоторому графу из  . Если класс   содержит только один граф  , то локально  -граф называется локально  -графом.

• Кликовым расширением графа   называется граф, полученный заменой каждой вершины   из   на полный подграф , содержащий не менее одной вершины, причем вершины из различных клик   и   смежны тогда и только тогда, когда вершины   и   смежны в  .

• Кликовое расширение графа   называется  -расширением  , если для любой вершины   подграф   содержит   вершин для некоторого фиксированного  .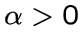

4 Реберные графы

• Граф   называется реберным графом графа  , если его вершинами служат ребра графа   и они смежны в графе  тогда и только тогда, когда имеют общую вершину в  .

• Треугольным графом   называется реберный граф полного графа с   вершинами.

• Граф на множестве пар   называется  -графом или решетчатым графом, если  ,  , а пары  и   смежны тогда и только тогда, когда  ,   или  ,  . Решетчатый  -граф является реберным графом полного двудольного графа  .

• Матрицей смежности   графа   на   вершинах называется   матрица  , строки и колонки которой занумерованы вершинами графа  , причем  , если   -- смежные вершины и  , если   -- несмежные вершины графа  .

• Собственными значениями графа   называются собственные значения его матрицы смежности  .

Известно, что наименьшее собственное значение треугольных и решетчатых графов равно  .

Отметим некоторые свойства треугольных и решетчатых графов, которые нам необходимы.

Пусть   является   графом. Перенумеруем вершины первой доли числами от   до  , а вершины второй доли числами от   до  . Множество всех вершин решетчатого  -графа  , который является реберным графом графа  , можно разложить в объединение   максимальных непересекающихся клик   по   вершин каждая. Клика  соответствует множеству ребер, исходящих из вершины с номером   первой доли графа  . Аналогично, множество всех вершин решетчатого графа можно разложить и в объединение   максимальных непересекающихся клик   по  вершин каждая. Клика   соответствует множеству ребер, исходящих из вершины с номером   второй доли графа  . Легко видеть, что   для всех  ,  , поскольку   соответствует единственному ребру соединяющему вершину   первой доли графа   с вершиной   второй доли графа  .

Таким образом, окрестность каждой вершины в решетчатом  -графе является объединением двух изолированных клик на  и   вершинах соответственно, то есть она изоморфна  .

В любом решетчатом  -графе   все его подграфы из   являются  -кокликами, а все его подграфы из  являются  -кликами или  -кликами.

Треугольный граф   является локально решетчатым   графом.

В любом треугольном графе   все его подграфы   изоморфны  , то есть являются четырехугольниками, а все его подграфы из   изоморфны  .