15. Теоретич. Оценки погрешности обобщённых формул трапеции и Симпсона.

Выведем формулу для погрешности данной квадратурной формулы.

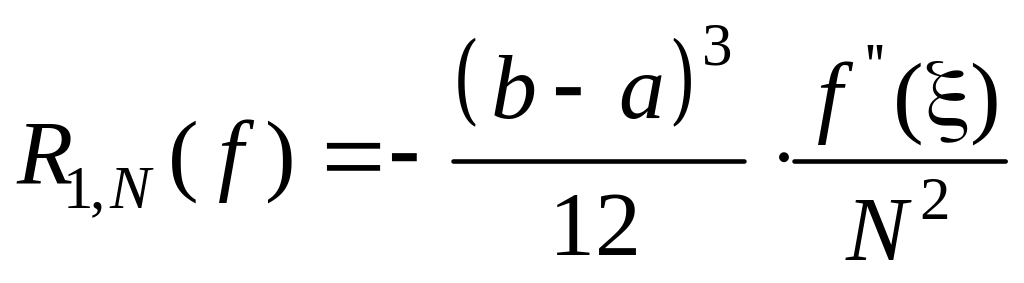Пусть и - равномерная сетка узлов с шагом , и , где определяется формулой (11). Тогда для погрешности обобщенной формулы трапеций справедлива формула: (14)

Обозначим погрешность базовой формулы трапеций на j-м интервале

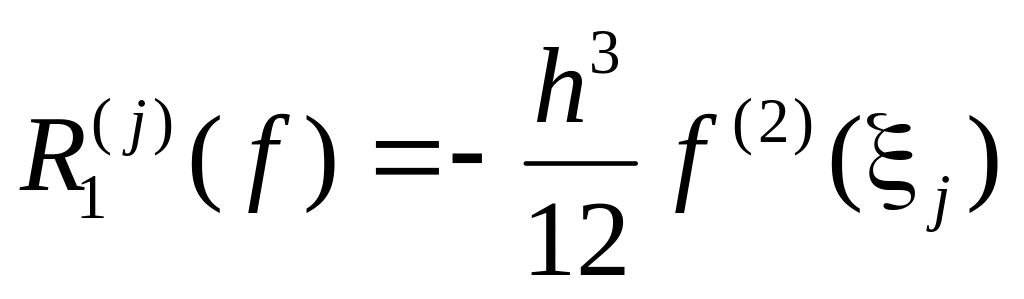, где , .

Просуммируем все j-ые погрешности по N интервалам:

.

Т.к. по условию , то непрерывна на . Отсюда следует, что функция 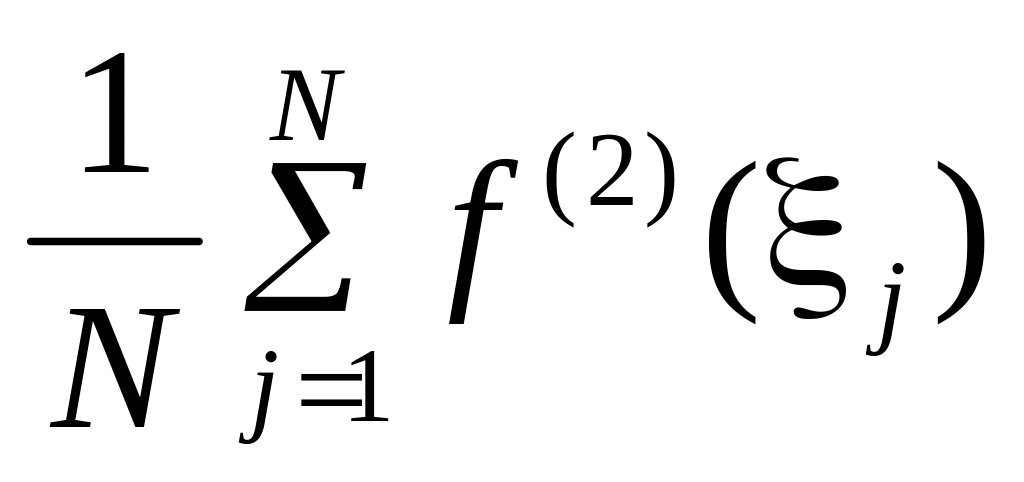так же непрерывна на , причем из условия следует, что .

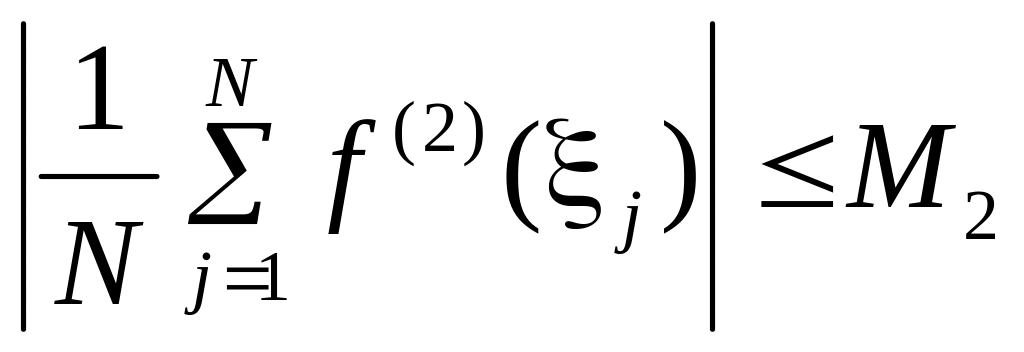Далее по теореме о промежуточном значении непрерывной на отрезке функции получаем, что найдется такая точка , что .

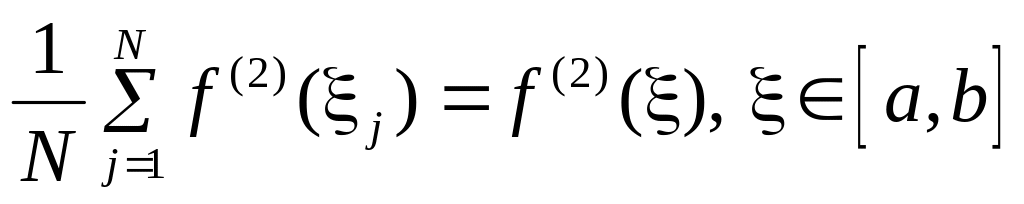Отсюда для погрешности формулы Ньютона-Котеса порядка 1 получаем:

.

(2)

В таком виде формула (14) демонстрирует степень зависимости погрешности от числа интервалов N.

Оценим погрешность обобщенной формулы Симпсона (15).

Пусть и -равномерная сетка узлов с шагом на . Тогда для погрешности обобщенной формулы Симпсона справедлива формула:

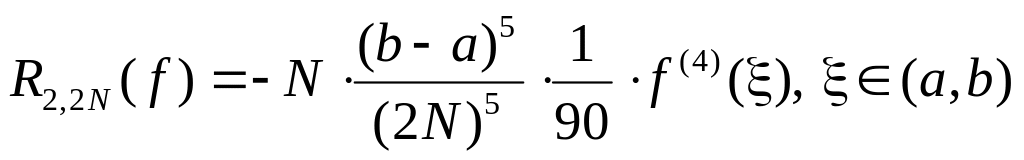. (16)

Теорема доказывается аналогично теореме 2.1, путем суммирования погрешностей на базовых отрезках

и использования теоремы Коши о промежуточном значении непрерывной функции на отрезке.

16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.

Обобщенная ф-ла Симпсона J_2,2N^*

Требуется обеспечивать выбор числа интервалов сетки (при последовательном удвоении числа интервалов разбиения) до достижения заданной точности. В качестве критерия остановки используется правило Рунге:

Если выполняется условие:

STOP:

точность достигнута. Приближенное значение интеграла . Здесь обозначено:

- значение интеграла для сетки с числом интервалов ; - то же - с числом интервалов .

Пример: Решить систему:

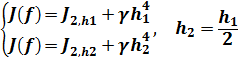
Найдем

Если

17. Общие свойства полиномов ортогональных с весом.

Пусть - система ортогональных с весом на отрезке полиномов. Справедливы следующие общие свойства таких полиномов.

1. Многочлен ортогонален любому алгебраическому многочлену m-ой степени при .

Действительно, многочлен можно единственным образом представить в виде линейной комбинации

.

(17)

Равенство (17) тождественное, поэтому коэффициенты единственным образом вычисляются путем приравнивания коэффициентов при соответствующих степенях x.

Умножая обе части (17) скалярно на , имеем:

в силу ортогональности .

2. Полином имеет на отрезке ровно n действительных и различных корней.

Заметим, что в силу теоремы Гаусса многочлен не может иметь более чем n корней (вообще говоря, комплексных).

Пусть имеет меньше, чем n простых действительных корней. Обозначим их . По этим точкам построим фундаментальный многочлен

Рассмотрим многочлен - многочлен степени , который имеет нули четной кратности. Следовательно, он сохраняет знак на . Отсюда следует, что

, т.е. , что противоречит свойству 1.

3. Для всех ортогональных многочленов, построенных на канонических промежутках с соответствующими весовыми функциями, существуют формулы Родрига и рекуррентные формулы. В частности, соответствующие формулы для полиномов Лагранжа приведены в лекции 5.

4. Система ортогональных с весом полиномов на - полна. Это значит, что не существует функции, отличной от нулевой и ортогональной всем функциям системы, т.е. из равенств 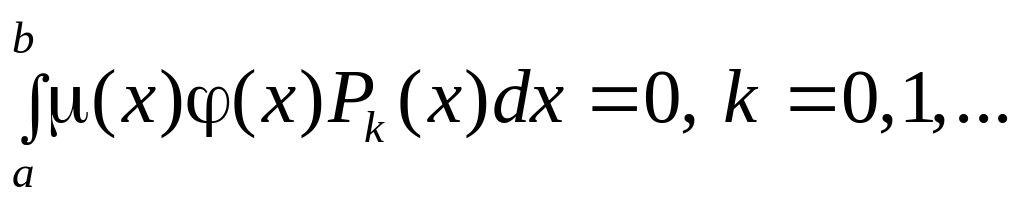следует, что на .