
- •2. Позиционная и нормализованная формы записи чисел. Значащие и верные цифры позиционной системы.
- •3. Ошибки округления чисел. Распространение ошибок округления в арифметических операциях. Абсолютная и относительная погрешность суммы, разности, произведения и частного.
- •Определение 2. Величина называется абсолютной погрешностью представления числа X с помощью числа .
- •4. Близость в метрическом и нормированном пространствах. Расстояние и норма, их определения и свойства. Основные классы функций:
- •5. Постановка задачи интерполяции. Интерполяционный многочлен Лагранжа. Теорема о погрешности интерполяции. Единственность многочлена Лагранжа.
- •6. Интерполяция на равномерной сетке. Конечные разности и их свойства.
- •1) Докажем, что операторы и перестановочные. .
- •7. Интерполяционный многочлен Ньютона. Построение и оценка погрешности.
- •8. Ортогональность в гильбертовом пространстве. Многочлены Чебышёва. Определение, построение, свойства.
- •9. Применение многочленов Чебышёва к задаче интерполяции. Теорема об оптимальном выборе узлов.
- •10. Среднеквадратичное приближение функций. Постановка задачи, теорема о существовании и единственности.
- •20. Классические ортогональные многочлены. Построение ортогональных многочленов на каноническом отрезке [-1,1].
- •11. Численное интегрирование. Использование функциональных рядов.
- •12. Квадратурная формула на основе интерполяции. Формулы дл коэффициентов и остаточного члена.
- •13. Базовые квадратурные формулы прямоугольников, трапеций и парабол. Формула теоретической погрешности.
- •14. Обобщенные квадратурные формулы трапеции и Симпсона (формулы Ньютона-Котеса).
- •15. Теоретич. Оценки погрешности обобщённых формул трапеции и Симпсона.
- •16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.
- •17. Общие свойства полиномов ортогональных с весом.
- •18. Алгебраическая степень точности квадратурной формулы. Квадратурные формулы Гаусса-Кристоффеля.
- •19. Теорема о необходимых и достаточных условиях выбора узлов в формулах Гаусса-Кристоффеля.
- •21. Принцип сжатых отображений. Теорема о неподвижной точке. Доказать единственность неподвижной точки. Следствия теоремы для банаховых пространств и пространства
- •22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.
- •23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.
- •24. Метод Ньютона в многомерном случае. Организация итерационного алгоритма.
- •25. Численные методы решения слау. Прямые и итерационные методы, общие понятия.
- •26. Нормы вещественных квадратных матриц. Спектральные свойства матриц.
- •27. Обусловленность матриц и систем лау. Число обусловленности в спектральной норме.
- •28. Метод итераций для слау специального вида. Теорема о достаточных условия сходимости.
- •29. Спектральный признак сходимости.(теорема о необх. И дост. Усл. Сходимости)
- •30.Стационарные итерационные процедуры. Приведение слау к системе специального вида.
- •31. Метод простых итераций Ричардсона. Условия сходимости.
- •32. Теорема о выборе ускоряющего множителя в методе Ричардсона.
- •33. Метод Якоби. Организация алгоритма. Теорема о достаточных условиях сходимости.
- •34. Метод Зейделя как ускорение метода Якоби. Организация алгоритма. Теорема об условиях сходимости.
- •35. Метод последовательной верхней релаксации. Задача выбора ускоряющего множителя.
- •36. Численное дифференцирование на основе интерполяции.
- •37. Численное дифференцирование на равномерной сетке, основанное на тэйлоровском разложении. Теорема об аппроксимации первой и второй производной.
- •38. Задача Коши. Постановка задачи. Сведение к системе для уравнения n-ого порядка.
- •39. Метод Эйлера. Алгоритм, геометрическая интерпретация, порядок точности.
- •40. Методы Рунге-Кутты повышенной точности. Метод «предиктор-корректор» и метод «средней точки».
- •41. Общая постановка краевой задачи для решения оду второго порядка. Классификация граничных условий.
- •42. Метод «стрельбы» решения краевой задачи с граничными условиями первого рода.
- •43. Метод конечных разностей решения линейной краевой задачи для оду второго порядка.
- •44. Каноническая разностная схема для линейного оду второго порядка, имеющая порядок аппроксимации .
- •45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.
5. Постановка задачи интерполяции. Интерполяционный многочлен Лагранжа. Теорема о погрешности интерполяции. Единственность многочлена Лагранжа.
Пусть дана сетка
узлов
![]() ,
где
,
где
![]() ,
и известны значения функции
,
и известны значения функции
![]() в узлах сетки:
в узлах сетки:
![]() ,
причем (n+1)
узловых
точек – попарно различны.
,
причем (n+1)
узловых
точек – попарно различны.
Интерполяция обобщенными полиномами.
Пусть известна
система линейно независимых функций
![]() .
Требуется найти такую линейную комбинацию
.
Требуется найти такую линейную комбинацию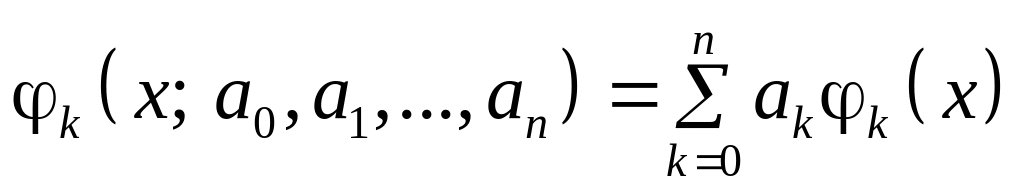
- «обобщенный
полином n-го
порядка», для которого выполняется
условие совпадения значений полинома
в узлах сетки со значениями
![]() .
Это требование приводит к системе
линейных уравнений:
.
Это требование приводит к системе
линейных уравнений:
|
(4) |
Систему (4) называют нормальной системой уравнений.
Для разрешимости системы (4) необходимо, чтобы определитель системы
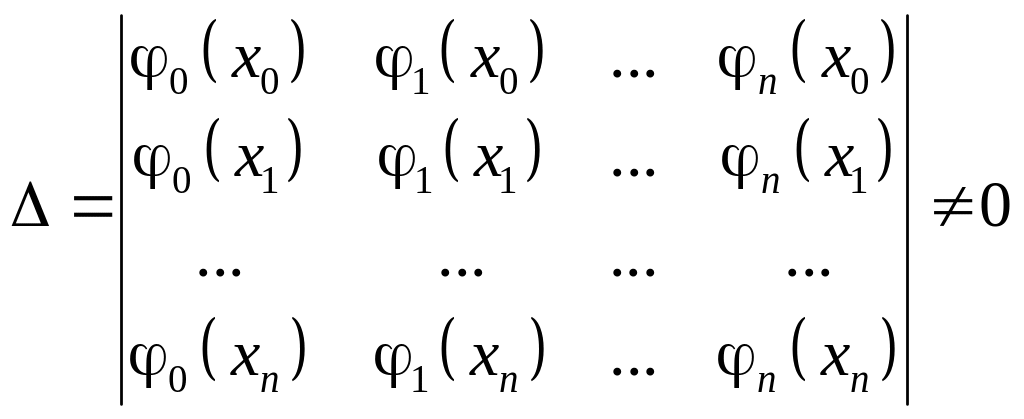 .
.
Рассмотрим частный случай задачи интерполяции – интерполяцию алгебраическими полиномами.
В этом случае в
качестве базисной системы функции
выступают степенные функции:
![]() .
.
Обозначим
![]() - искомый интерполяционный полином n-ой
степени
- искомый интерполяционный полином n-ой
степени
![]() ,
и запишем условия совпадения значений
полинома с табличными значениями функции
,
и запишем условия совпадения значений
полинома с табличными значениями функции
![]() :
: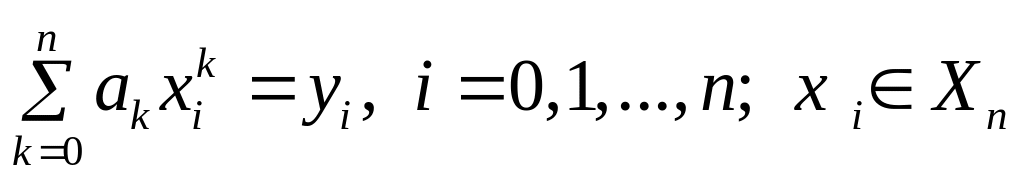 .(5)
.(5)
Определитель этой системы - определитель Вандермонда – отличен от нуля:
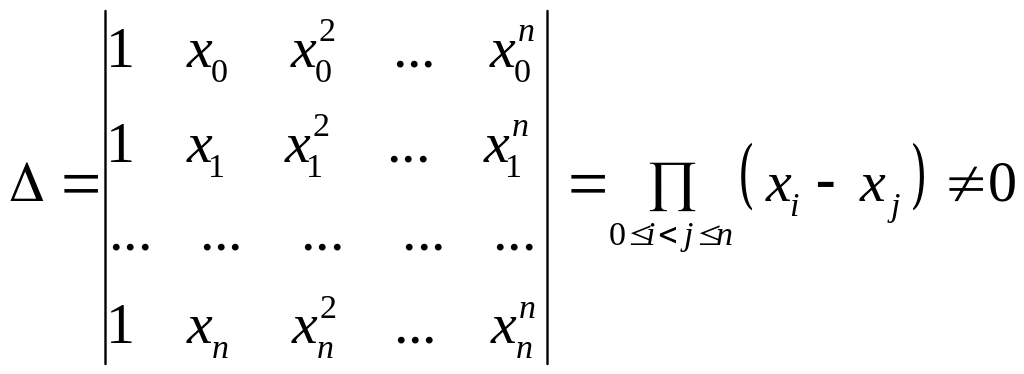 ,
,
поэтому система имеет единственное решение.
Система (5) плохо
обусловлена.
Покажем, как можно построить искомый
интерполяционный полином другим
способом, не решая систему. Для этого
построим так называемые фундаментальные
полиномы
степени n:
![]() ,
удовлетворяющие условию:
,
удовлетворяющие условию:
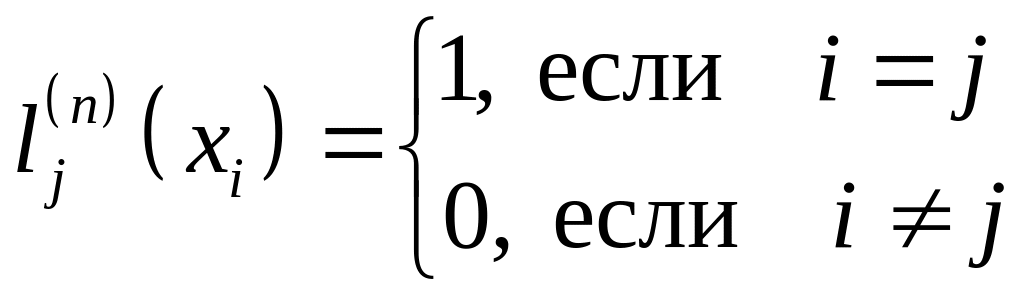 . (6)
. (6)
Нетрудно убедиться,
что указанным свойством обладает полином
следующего вида:
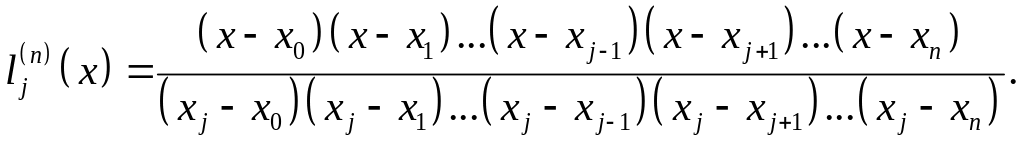
Условие (6)
непосредственно проверяется. Отсюда
следует, что искомый (7) интерполяционный
полином
![]() можно записать в виде:
можно записать в виде:
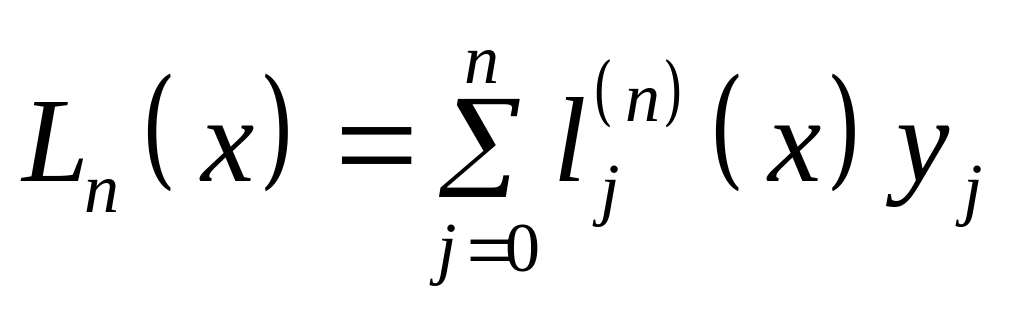
Очевидно, что в
силу свойства фундаментальных полиномов,
![]() Полученный таким способом полином
называют интерполяционным
полиномом Лагранжа.
Полученный таким способом полином
называют интерполяционным
полиномом Лагранжа.
Приведем еще одно доказательство единственности полинома Лагранжа (7) независимо от логики решения нормальной системы (2).
Теорема 1.1. Полином
Лагранжа
![]() (4), проходящий через все табличные (n+1)
значения функции y(x)
– единственный.
(4), проходящий через все табличные (n+1)
значения функции y(x)
– единственный.
![]() От противного.
Пусть
От противного.
Пусть
![]() еще
один полином
еще
один полином
![]() степени n,
решающий ту же задачу интерполяции.
Рассмотрим разность
степени n,
решающий ту же задачу интерполяции.
Рассмотрим разность
![]() - полином порядка
- полином порядка
![]() .
Очевидно, что этот полином имеет на
отрезке
.
Очевидно, что этот полином имеет на
отрезке
![]() ровно (n+1)
корень, что противоречит основной
теореме алгебры. Значит,
ровно (n+1)
корень, что противоречит основной
теореме алгебры. Значит,
![]()
Теорема 1.2. (О
погрешности интерполяции).
Пусть функция
![]()
![]() ,
задана сетка узлов
,
задана сетка узлов
![]() ,
– интерполяционный полином Лагранжа
(4), построенный по значениям функции
y(x)
в узлах сетки Xn.
Тогда для погрешности интерполяции
справедливы следующие оценки:
,
– интерполяционный полином Лагранжа
(4), построенный по значениям функции
y(x)
в узлах сетки Xn.
Тогда для погрешности интерполяции
справедливы следующие оценки:
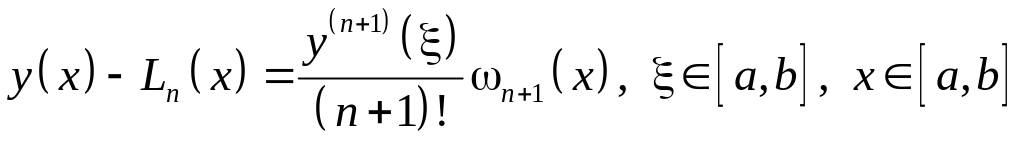 - (8)
- (8)
– теоретическая
погрешность в точке
|
|
|
(9) |
|
(10) |
– максимальная абсолютная погрешность на всем отрезке,
где
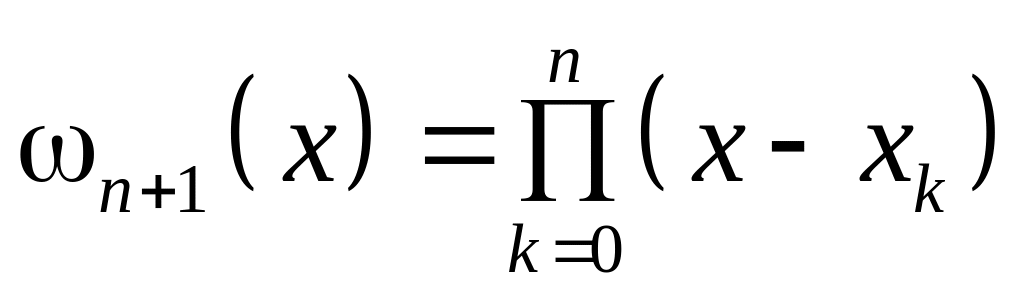 – специальный полином (n+1)-ой
степени, построенный по узлам как по
нулям;
– специальный полином (n+1)-ой
степени, построенный по узлам как по
нулям;
![]() – существует в силу определения класса
функций
– существует в силу определения класса
функций
![]() .
.
![]() Запишем y(x)
в виде:
Запишем y(x)
в виде:
![]() ,
где
,
где
![]() – погрешность интерполяции в точке
.
Очевидно по условию, что
– погрешность интерполяции в точке
.
Очевидно по условию, что
![]() .
.
Отсюда следует,
что погрешность (остаточный член)
интерполяции можно искать в виде:
![]() ,
где r
,
где r![]() –
некоторая функция.
–
некоторая функция.
Зафиксируем точку
![]() и рассмотрим вспомогательную функцию
и рассмотрим вспомогательную функцию
|
(11) |
где t – свободная переменная. Положим в (11) t=x.
![]() Т.е.
функция обращается в 0 в точке t=x.
Положим далее последовательно
Т.е.
функция обращается в 0 в точке t=x.
Положим далее последовательно
![]() Получаем:
Получаем:
 .
.
Т.о. мы получили,
что на отрезке
![]() функция
функция
![]() обращается в 0 ровно в (n+2)
точках. Отсюда
по теореме Ролля следует, что на интервале
(a,b)
обращается в 0 ровно в (n+2)
точках. Отсюда
по теореме Ролля следует, что на интервале
(a,b)
существует, по крайней мере, (n+1) точка, в которой
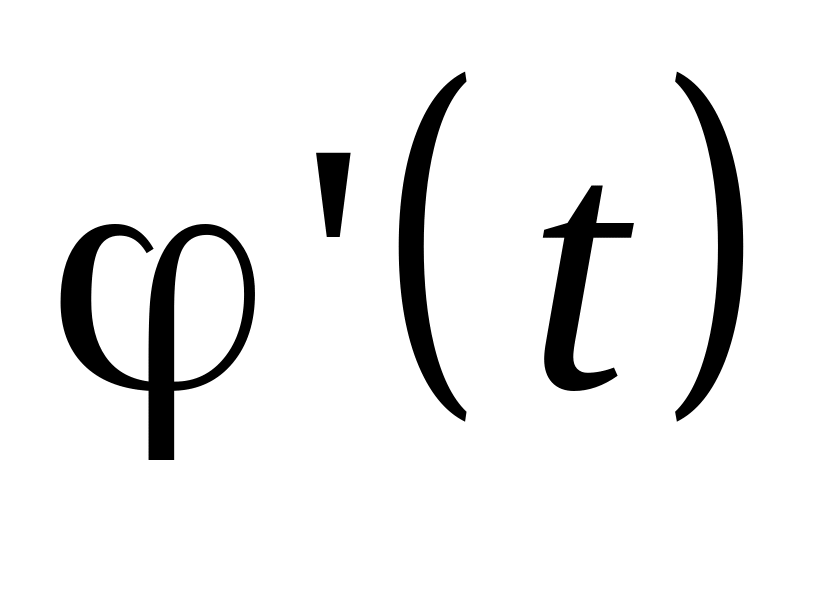 обращается в 0;
обращается в 0;существует, по крайней мере, n точек, в которых
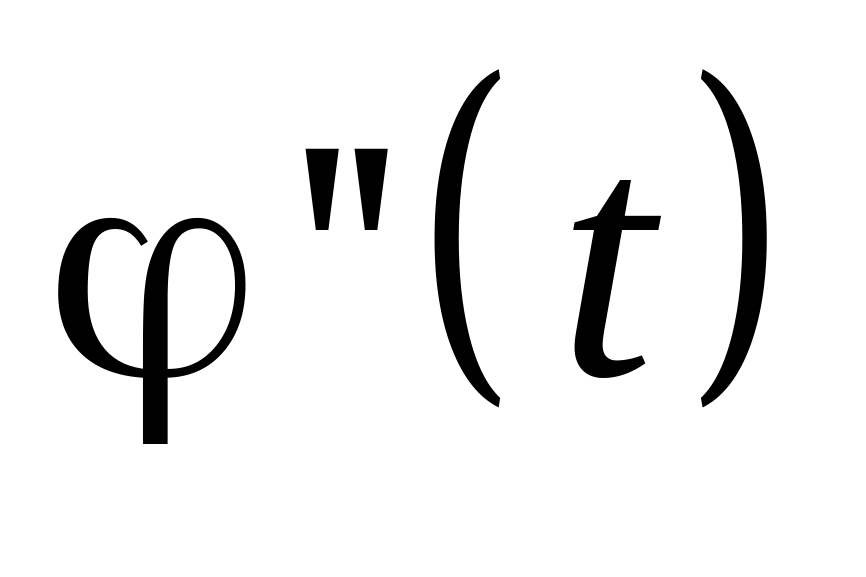 обращается в 0;
обращается в 0;………………………
существует, по крайней мере, 1 точка
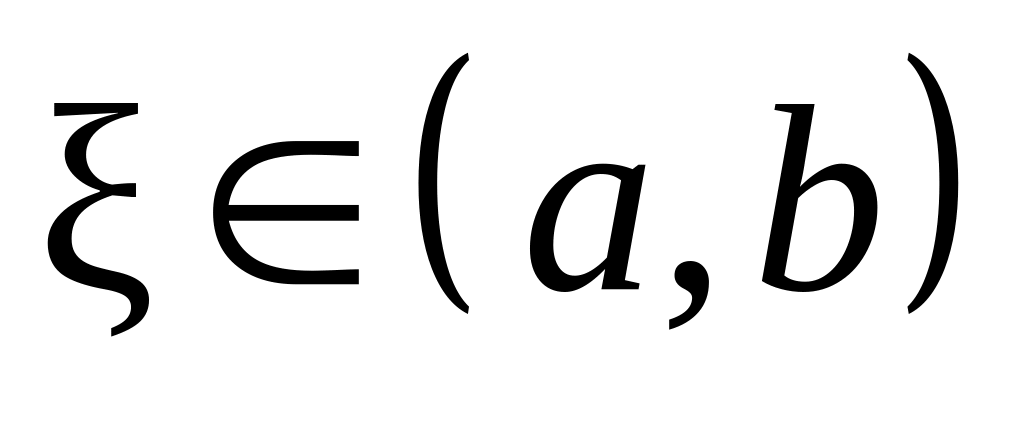 ,
в которой
,
в которой
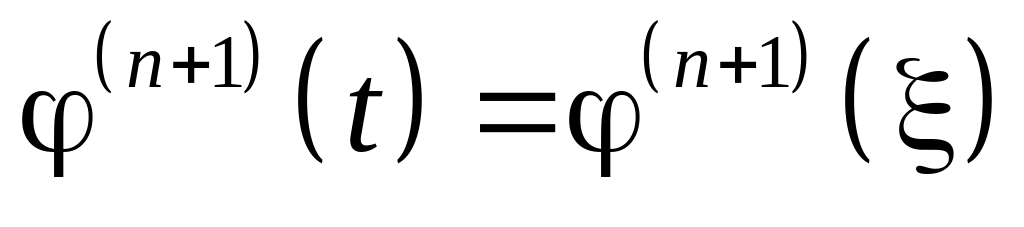 обращается в 0.
обращается в 0.
Продифференцируем
формулу (11) по t
n+1
раз и положим
![]() .
Получим:
.
Получим:
|
(12) |
Учтем, что
![]() ,
т.к. степень полинома равна n.
Далее получаем:
,
т.к. степень полинома равна n.
Далее получаем:
![]() ,
т.к.
,
т.к.
![]() - многочлен
- многочлен
![]() -ой
степени специального вида с коэффициентом
при старшей степени, равным 1.
-ой
степени специального вида с коэффициентом
при старшей степени, равным 1.
Подставляя эти
результаты в (12), получаем:
![]()
откуда следует
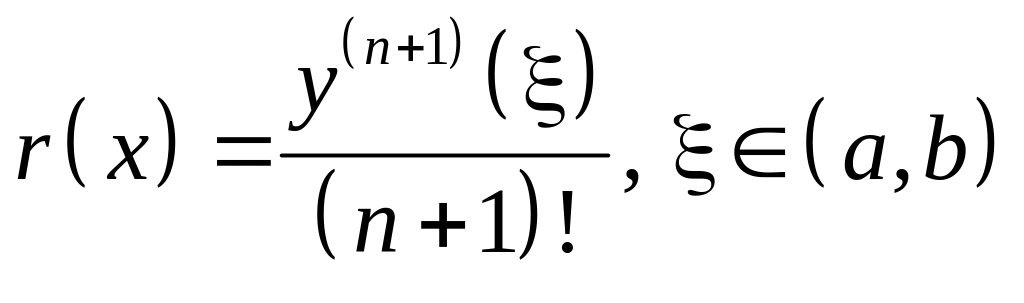 .
Подставляя в выражение для
.
Подставляя в выражение для
![]() ,
получаем
,откуда
следует формула (8). Оценки (9), (10) вытекают
из (8) автоматически.
,
получаем
,откуда
следует формула (8). Оценки (9), (10) вытекают
из (8) автоматически.
![]()

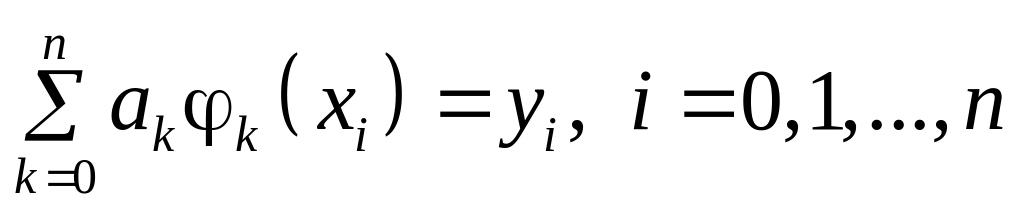 .
. – абсолютная
погрешность в точке,
– абсолютная
погрешность в точке,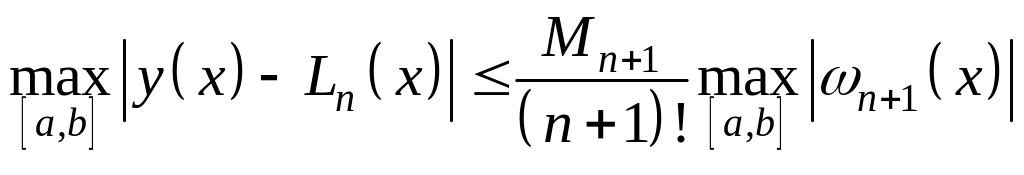 -
-