
- •2. Позиционная и нормализованная формы записи чисел. Значащие и верные цифры позиционной системы.
- •3. Ошибки округления чисел. Распространение ошибок округления в арифметических операциях. Абсолютная и относительная погрешность суммы, разности, произведения и частного.
- •Определение 2. Величина называется абсолютной погрешностью представления числа X с помощью числа .
- •4. Близость в метрическом и нормированном пространствах. Расстояние и норма, их определения и свойства. Основные классы функций:
- •5. Постановка задачи интерполяции. Интерполяционный многочлен Лагранжа. Теорема о погрешности интерполяции. Единственность многочлена Лагранжа.
- •6. Интерполяция на равномерной сетке. Конечные разности и их свойства.
- •1) Докажем, что операторы и перестановочные. .
- •7. Интерполяционный многочлен Ньютона. Построение и оценка погрешности.
- •8. Ортогональность в гильбертовом пространстве. Многочлены Чебышёва. Определение, построение, свойства.
- •9. Применение многочленов Чебышёва к задаче интерполяции. Теорема об оптимальном выборе узлов.
- •10. Среднеквадратичное приближение функций. Постановка задачи, теорема о существовании и единственности.
- •20. Классические ортогональные многочлены. Построение ортогональных многочленов на каноническом отрезке [-1,1].
- •11. Численное интегрирование. Использование функциональных рядов.
- •12. Квадратурная формула на основе интерполяции. Формулы дл коэффициентов и остаточного члена.
- •13. Базовые квадратурные формулы прямоугольников, трапеций и парабол. Формула теоретической погрешности.
- •14. Обобщенные квадратурные формулы трапеции и Симпсона (формулы Ньютона-Котеса).
- •15. Теоретич. Оценки погрешности обобщённых формул трапеции и Симпсона.
- •16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.
- •17. Общие свойства полиномов ортогональных с весом.
- •18. Алгебраическая степень точности квадратурной формулы. Квадратурные формулы Гаусса-Кристоффеля.
- •19. Теорема о необходимых и достаточных условиях выбора узлов в формулах Гаусса-Кристоффеля.
- •21. Принцип сжатых отображений. Теорема о неподвижной точке. Доказать единственность неподвижной точки. Следствия теоремы для банаховых пространств и пространства
- •22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.
- •23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.
- •24. Метод Ньютона в многомерном случае. Организация итерационного алгоритма.
- •25. Численные методы решения слау. Прямые и итерационные методы, общие понятия.
- •26. Нормы вещественных квадратных матриц. Спектральные свойства матриц.
- •27. Обусловленность матриц и систем лау. Число обусловленности в спектральной норме.
- •28. Метод итераций для слау специального вида. Теорема о достаточных условия сходимости.
- •29. Спектральный признак сходимости.(теорема о необх. И дост. Усл. Сходимости)
- •30.Стационарные итерационные процедуры. Приведение слау к системе специального вида.
- •31. Метод простых итераций Ричардсона. Условия сходимости.
- •32. Теорема о выборе ускоряющего множителя в методе Ричардсона.
- •33. Метод Якоби. Организация алгоритма. Теорема о достаточных условиях сходимости.
- •34. Метод Зейделя как ускорение метода Якоби. Организация алгоритма. Теорема об условиях сходимости.
- •35. Метод последовательной верхней релаксации. Задача выбора ускоряющего множителя.
- •36. Численное дифференцирование на основе интерполяции.
- •37. Численное дифференцирование на равномерной сетке, основанное на тэйлоровском разложении. Теорема об аппроксимации первой и второй производной.
- •38. Задача Коши. Постановка задачи. Сведение к системе для уравнения n-ого порядка.
- •39. Метод Эйлера. Алгоритм, геометрическая интерпретация, порядок точности.
- •40. Методы Рунге-Кутты повышенной точности. Метод «предиктор-корректор» и метод «средней точки».
- •41. Общая постановка краевой задачи для решения оду второго порядка. Классификация граничных условий.
- •42. Метод «стрельбы» решения краевой задачи с граничными условиями первого рода.
- •43. Метод конечных разностей решения линейной краевой задачи для оду второго порядка.
- •44. Каноническая разностная схема для линейного оду второго порядка, имеющая порядок аппроксимации .
- •45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.
20. Классические ортогональные многочлены. Построение ортогональных многочленов на каноническом отрезке [-1,1].
Рассмотрим систему
алгебраических многочленов
![]() (34)
(34)
Такая система,
рассматриваемая в гильбертовом
пространстве
![]() ,
линейно независима при
,
линейно независима при
![]() .
Однако, непосредственная подстановка
алгебраических многочленов в систему
(30) неэффективна, т.к. приводит к плохо
обусловленной системе уравнений. На
базе системы (34) можно построить
ортогональные полиномы на заданном
отрезке (или бесконечном промежутке) с
заданной весовой функцией
.
Однако, непосредственная подстановка
алгебраических многочленов в систему
(30) неэффективна, т.к. приводит к плохо
обусловленной системе уравнений. На
базе системы (34) можно построить
ортогональные полиномы на заданном
отрезке (или бесконечном промежутке) с
заданной весовой функцией
![]() .Рассмотрим
один из алгоритмов ортогонализации,
известный как рекуррентная
процедура Грама-Шмидта. Новая
система полиномов, ортогональная на
с весом
строится рекуррентно:
.Рассмотрим
один из алгоритмов ортогонализации,
известный как рекуррентная
процедура Грама-Шмидта. Новая
система полиномов, ортогональная на
с весом
строится рекуррентно:
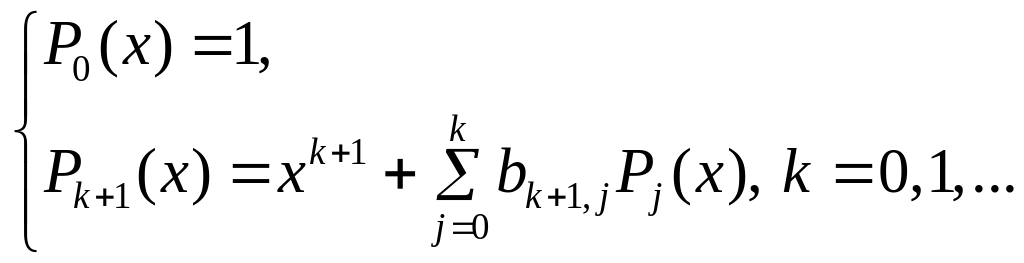 .
.
Накладывая условие
ортогональности:
![]() ,
,
![]() получаем формулу для коэффициентов
получаем формулу для коэффициентов
![]() :
:
|
(35) |
Пример 16.
Пусть отрезок
![]() .
Построить первые три ортогональных
полинома
.
Построить первые три ортогональных
полинома
![]() ,
используя процедуру Грама-Шмидта.
,
используя процедуру Грама-Шмидта.
Полагаем
![]() .
Далее по формулам (35) находим
.
Далее по формулам (35) находим
 откуда получаем
откуда получаем
![]() Действуя аналогично далее, получаем:
Действуя аналогично далее, получаем:
![]() .
.
Существует другой
- более эффективный способ построения
ортогональных многочленов. В частности,
для системы ортогональных многочленов
на отрезке
с весом
![]() ,
справедливы следующие две формулы:
,
справедливы следующие две формулы:
формула Родрига:
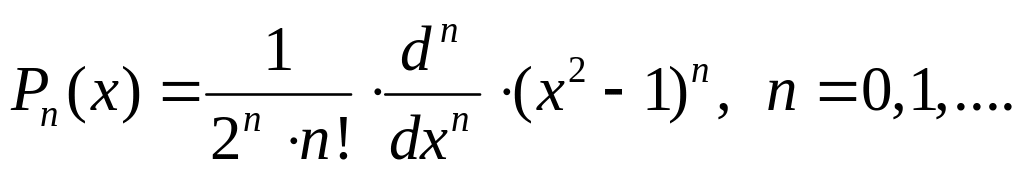 (36)
(36)
и рекуррентная
формула:
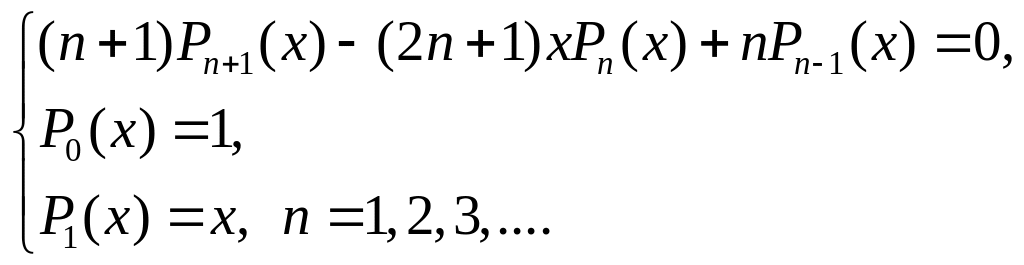 (37)
(37)
Из (36) последовательно
получаем:
![]() ;
Далее по рекуррентной формуле (37) при
;
Далее по рекуррентной формуле (37) при
![]() находим:
находим:
![]() .
Получаемые таким образом полиномы
называются полиномами
Лежандра.
.
Получаемые таким образом полиномы
называются полиномами
Лежандра.
Замечание. Найденные по процедуре (36)-(37) ортогональные многочлены могут лишь множителями отличаться от тех, которые строятся по методу Грама-Шмидта.
Квадрат нормы
полиномов Лежандра равен
![]()
11. Численное интегрирование. Использование функциональных рядов.
Пусть
![]() .
Тогда существует определенный интеграл
.
Тогда существует определенный интеграл
 ,
,
согласно формуле Лейбница.
Однако во многих
случаях первообразная
![]() не выражается в аналитическом виде,
поэтому приходится применять те или
иные численные методы.
не выражается в аналитическом виде,
поэтому приходится применять те или
иные численные методы.
Примеры «неберущихся» интегралов:
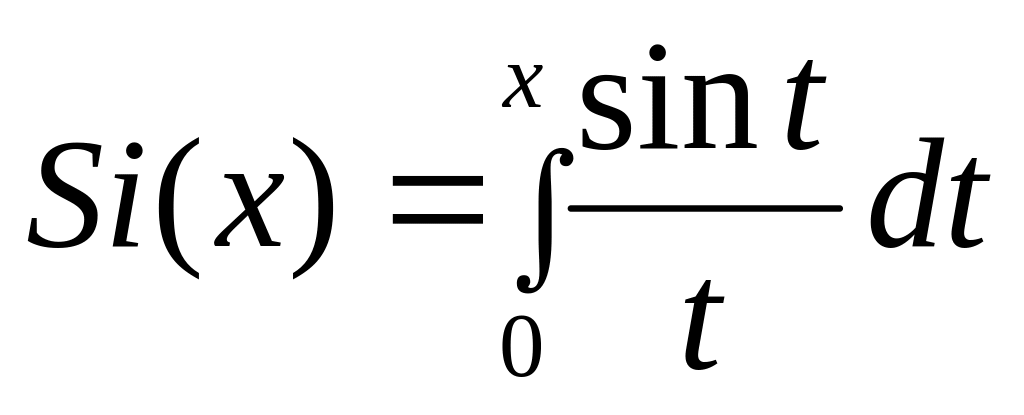 – интегральный
синус;
– интегральный
синус;
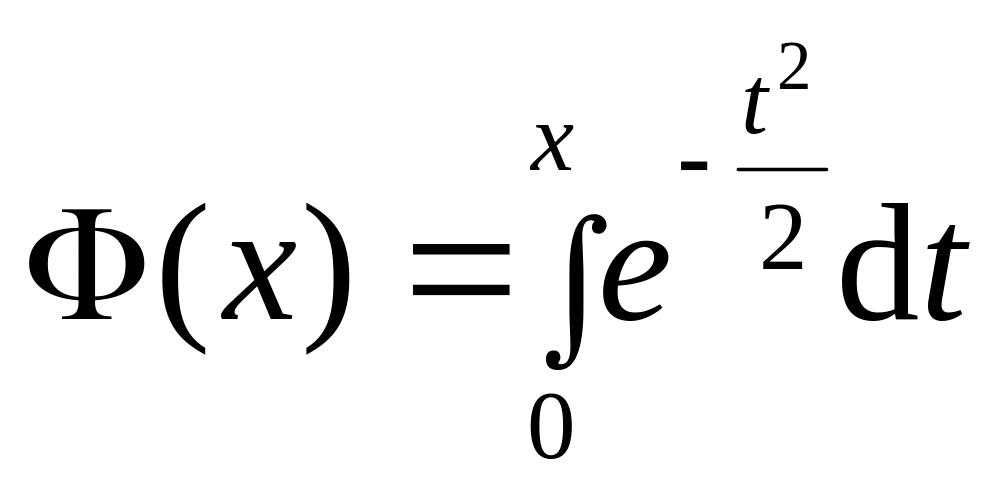 –
интеграл вероятности;
–
интеграл вероятности;
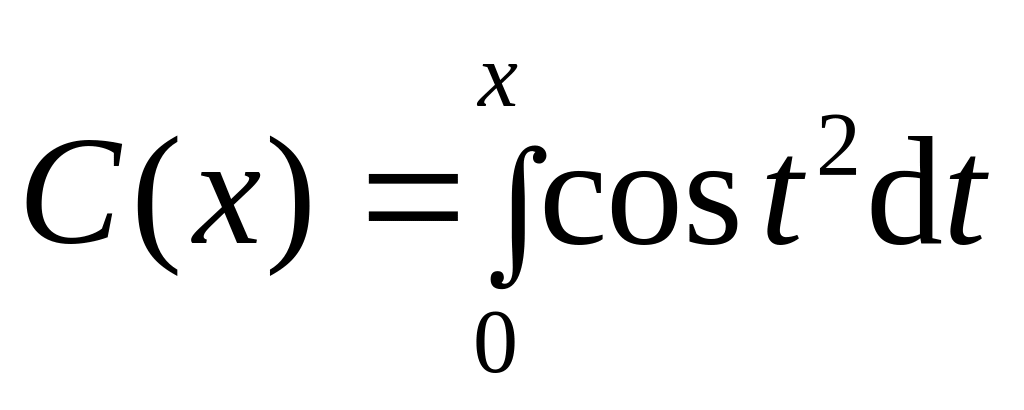 - интеграл Френеля,
и другие.
- интеграл Френеля,
и другие.
Одним из способов численного интегрирования является разложение подынтегральной функции в те или иные ряды (например, в ряд Тейлора) и почленное интегрирование полученного ряда. Например, для «интегрального синуса» получаем с помощью тейлоровского разложения:
 .
.
Взяв конечное
число членов разложения, получим
приближенное значение интегрального
синуса
![]() .
При этом абсолютная ошибка приближения
оценивается по остаточному члену
тейлоровского разложения.
.
При этом абсолютная ошибка приближения
оценивается по остаточному члену
тейлоровского разложения.
Подобные примеры рассматриваются на семинарском занятии.
Другой подход основан на интерполяции подынтегральной функции по Лагранжу или Ньютону. В результате получаются так называемые квадратурные формулы. В следующем параграфе этот подход рассматривается более подробно.
12. Квадратурная формула на основе интерполяции. Формулы дл коэффициентов и остаточного члена.
Пусть задана сетка
узлов
![]() ,
не обязательно равномерная. Требуется
приближенно вычислить интеграл
,
не обязательно равномерная. Требуется
приближенно вычислить интеграл
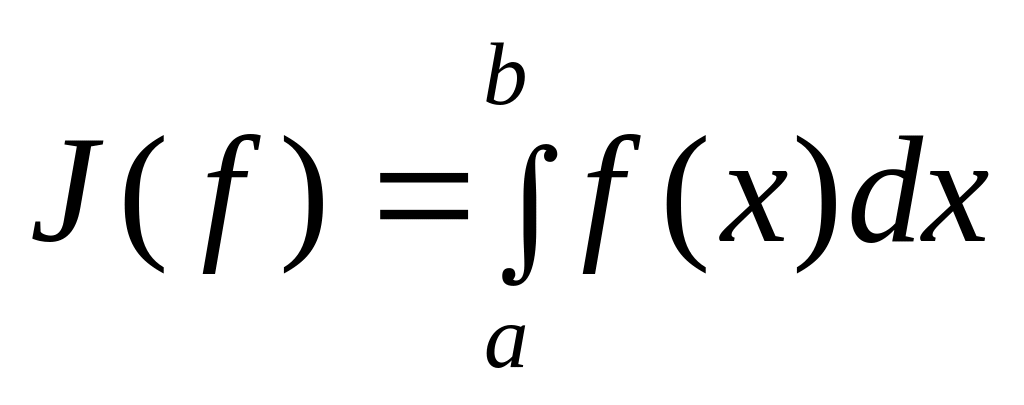 .
Представим подынтегральную функцию
интерполяционным полиномом Лагранжа
по данной системе узлов:
.
Представим подынтегральную функцию
интерполяционным полиномом Лагранжа
по данной системе узлов:
![]() ,
тогда
,
тогда
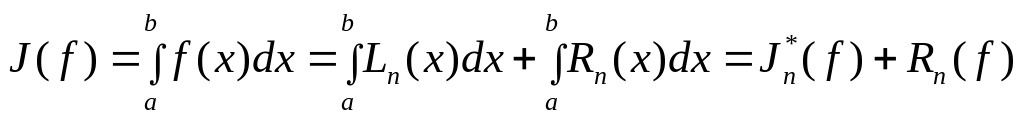 ,
где
,
где
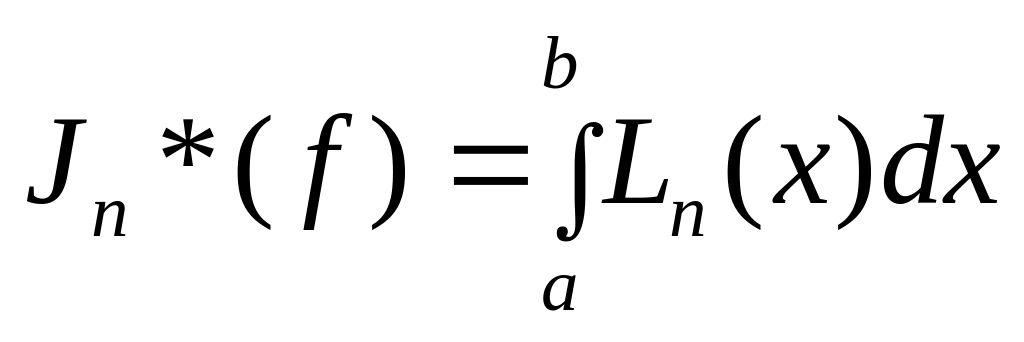 - приближенное значение интеграла,
- приближенное значение интеграла,
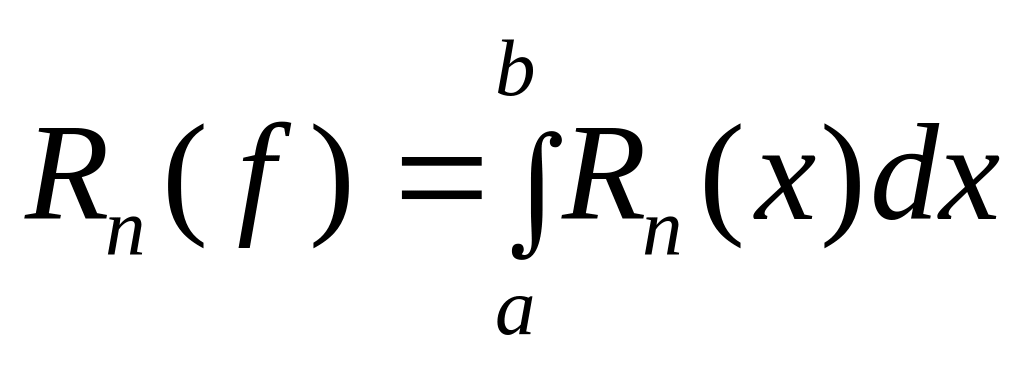 - ошибка приближения.
- ошибка приближения.
Используя
представление полинома Лагранжа через
фундаментальные полиномы
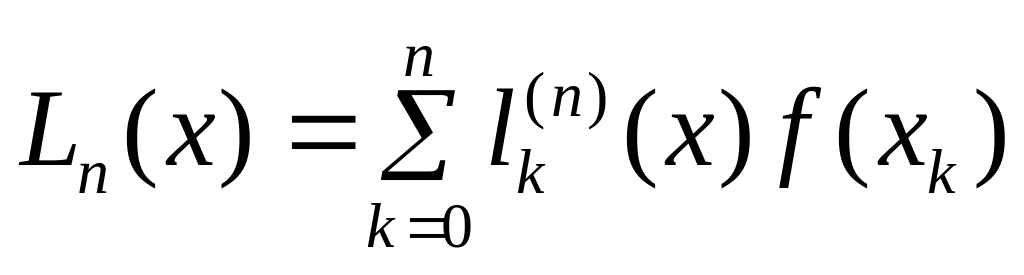 ,
получим:
,
получим:
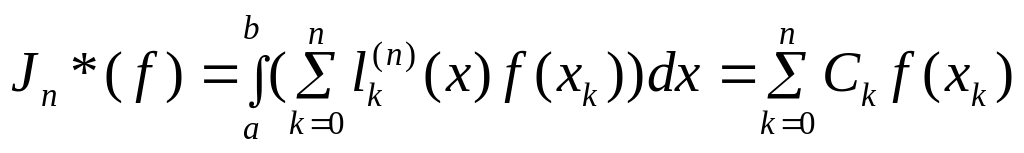 (1)
(1)
Где
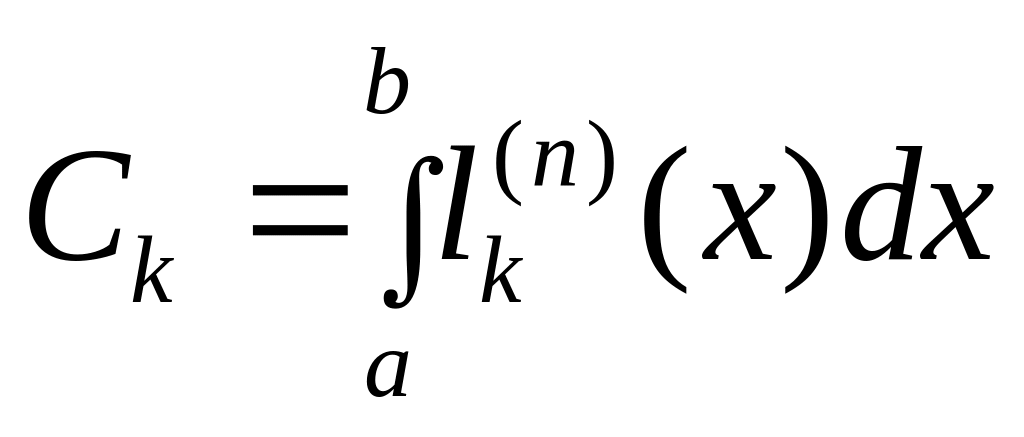 .
.
Формула (1) называется
квадратурной формулой n-го
порядка. Если
![]() ,
то используя формулу погрешности
интерполяции в точке, получим следующее
выражение для погрешности квадратурной
формулы:
,
то используя формулу погрешности
интерполяции в точке, получим следующее
выражение для погрешности квадратурной
формулы:
|
(2) |
Оценивая обе части (2) по модулю, получим оценку абсолютной погрешности
|
(3) |
Где
![]() ,
,
![]() Стандартные квадратурные формулы
получаются для равномерной сетки
Стандартные квадратурные формулы
получаются для равномерной сетки
![]() .
.
Воспользуемся первой интерполяционной формулой Ньютона:
|
(4) |
где
![]() .
.
В этом случае
квадратурная формула n-го
порядка получается при подстановке
представления (4) в интеграл
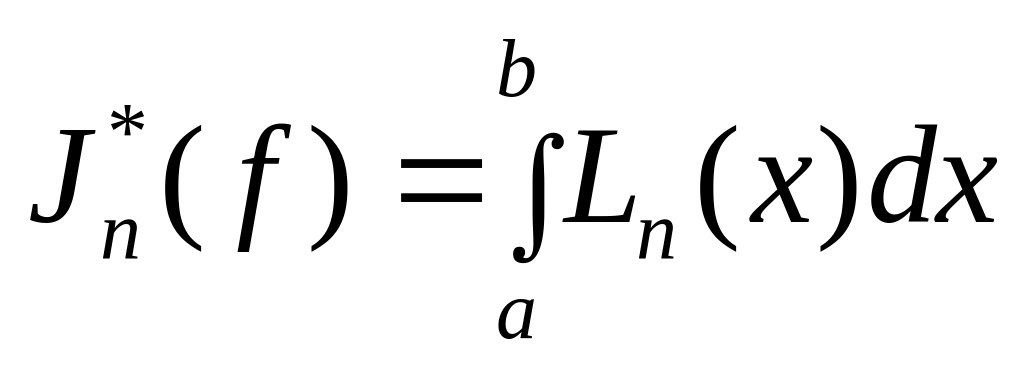 и представления конечных разностей
и представления конечных разностей
![]() в виде линейной комбинации узловых
значений функции
в виде линейной комбинации узловых
значений функции
![]() (согласно свойству конечных разностей).
Для ошибки квадратурной формулы n-го
порядка соответственно получаем
выражение:
(согласно свойству конечных разностей).
Для ошибки квадратурной формулы n-го
порядка соответственно получаем
выражение:
|
(5) |
После замены
переменной
![]() ,
окончательно получаем:
,
окончательно получаем:
|
(5) |
Условие
![]() связано с тем, что при
связано с тем, что при
![]() понятие «шага» сетки не определено.
понятие «шага» сетки не определено.


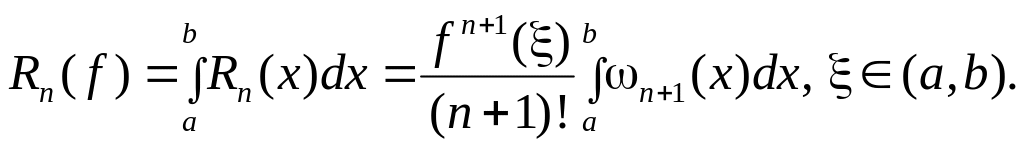
 ,
,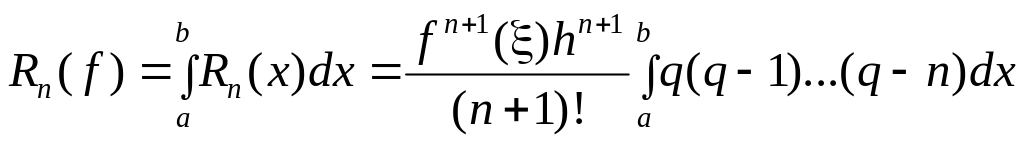 .
.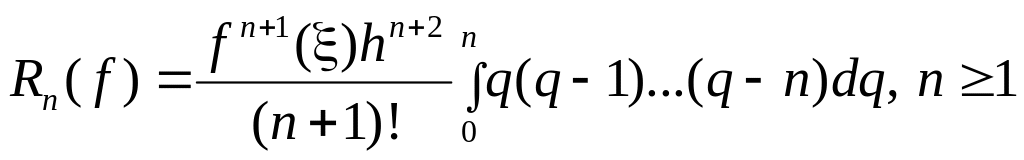 .
.