44. Каноническая разностная схема для линейного оду второго порядка, имеющая порядок аппроксимации .

Рассмотрим один из вариантов аппроксимации краевого условия третьего рода на левом конце отрезка.

Граничное условие третьего рода имеет вид (см. урав.(18)):

(24)

Разложим функцию по Тэйлору с центром в точке и найдем значение :

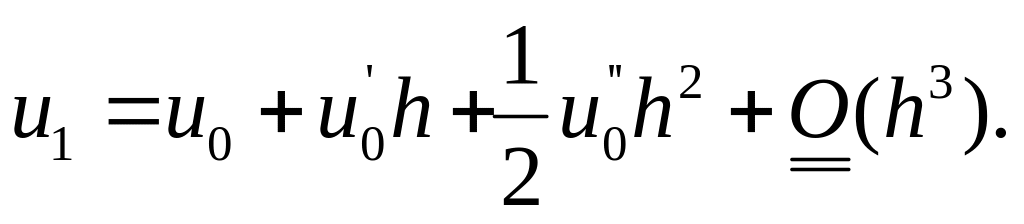
найдем из уравнения (21), аппроксимируя его в точке сетки (непрерывность вторых производных на отрезке позволяет это сделать):

.

Подставляя найденное значение второй производной в выражение для , получаем:

.

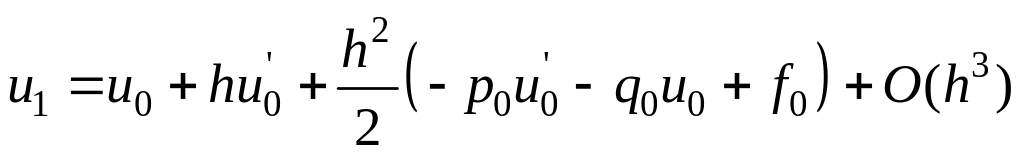Отбрасывая остаточный член и приводя подобные в последнем уравнении, получаем систему линейных уравнений для неизвестных :

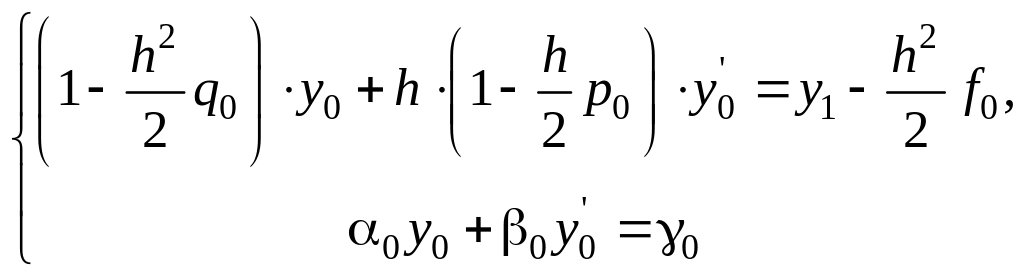
Исключая из полученной системы , получаем линейное уравнение, связывающее два сеточных значения и :

,

где параметры легко выражаются через . Аналогично аппроксимируется третье краевое условие на правом конце отрезка, которое приводится к виду

.

В результате получаем неявную конечно-разностную систему уравнений, записанную в каноническом виде:

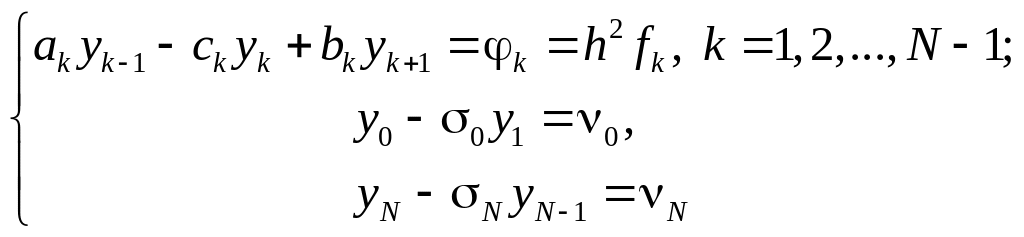(25)

Система (25) - трехдиагональная, для которой разработаны специальные эффективные методы численного решения, например, метод прогонки [1,6,11].

45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.

Пусть

(26)

Апроксимируем (1) на сетке с шагом . Тогда

(27)

Определение 1. Говорят, что задача (27) апроксимирует задачу (26) на сетке с порядком относительно шага , если выполняется условие: , где константа не зависит от . Заметим, что по определению сеточного решения . С другой стороны, , т.к. при подстановке точного решения в левую часть сеточного уравнения системы (27), получим несколько иную сеточную правую часть. Поэтому, обозначив - “невязка”, получаем: - - по условию аппроксимация порядка p.

Итак

(28)

Определение 2. Пусть

(29)

невозмущенная задача на сетке, - возмущенная задача..

Разностная схема (29) устойчива по правой части, если малое изменение “правой части” ( ) приводит к малому изменению решения, т.е. если где с₂ не зависит от h.

Теорема 4.5. (Необходимый и достаточный признак устойчивости процедуры (31) по правой части). Итерационная процедура устойчива по правой части тогда и только тогда, когда выполняется условие , где с не зависит от h (т.е. от N). Без доказательства (см.[1,2]).

Однако это условие не всегда легко проверить. Поэтому для конкретных итерационных схем вырабатываются и доказываются более простые достаточные условия. Таковы, например, условия “диагонального преобладания” для схем прогонки.

Теорема 4.6. (Необходимый спектральный признак устойчивости). Пусть - собственные числа оператора R_h. Для устойчивости схемы (31) по правой части необходимо выполнение условия:

, (32) причем константа не зависит от h (от N).

Пусть (32) не выполняется для некоторого собственного значения . То есть, не существует такой константы , для которой (32) выполнялось бы для данного ₁. Фактически, это означает, что вместо линейного ограничения имеем:

, где 0<<1, c₁ - некоторая константа.

Пусть - соответствующий собственный вектор, т.е.

Оценим по сеточной норме:

.

Из последнего неравенства следует:

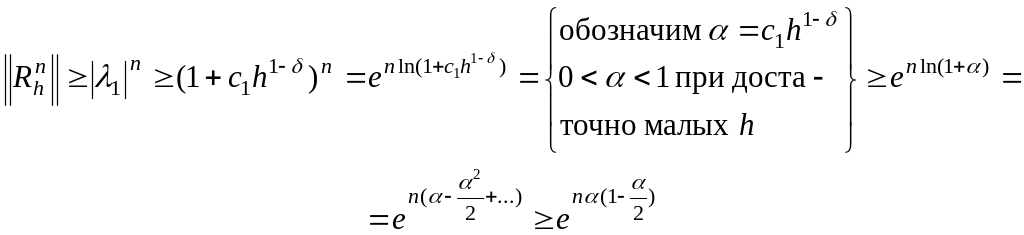
Заметим, что по условию на , поэтому

т.е. нарушается условие устойчивости, сформулированное ранее. Происходит экспоненциальный рост ошибки.

Рассмотрим снова сеточное уравнение вида (31)

63