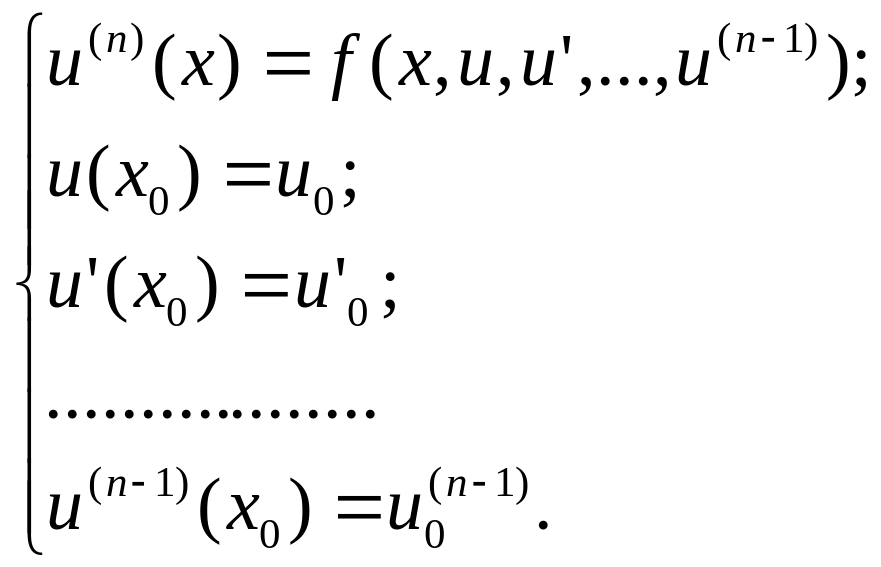- •2. Позиционная и нормализованная формы записи чисел. Значащие и верные цифры позиционной системы.
- •3. Ошибки округления чисел. Распространение ошибок округления в арифметических операциях. Абсолютная и относительная погрешность суммы, разности, произведения и частного.
- •Определение 2. Величина называется абсолютной погрешностью представления числа X с помощью числа .
- •4. Близость в метрическом и нормированном пространствах. Расстояние и норма, их определения и свойства. Основные классы функций:
- •5. Постановка задачи интерполяции. Интерполяционный многочлен Лагранжа. Теорема о погрешности интерполяции. Единственность многочлена Лагранжа.
- •6. Интерполяция на равномерной сетке. Конечные разности и их свойства.
- •1) Докажем, что операторы и перестановочные. .
- •7. Интерполяционный многочлен Ньютона. Построение и оценка погрешности.
- •8. Ортогональность в гильбертовом пространстве. Многочлены Чебышёва. Определение, построение, свойства.
- •9. Применение многочленов Чебышёва к задаче интерполяции. Теорема об оптимальном выборе узлов.
- •10. Среднеквадратичное приближение функций. Постановка задачи, теорема о существовании и единственности.
- •20. Классические ортогональные многочлены. Построение ортогональных многочленов на каноническом отрезке [-1,1].
- •11. Численное интегрирование. Использование функциональных рядов.
- •12. Квадратурная формула на основе интерполяции. Формулы дл коэффициентов и остаточного члена.
- •13. Базовые квадратурные формулы прямоугольников, трапеций и парабол. Формула теоретической погрешности.
- •14. Обобщенные квадратурные формулы трапеции и Симпсона (формулы Ньютона-Котеса).
- •15. Теоретич. Оценки погрешности обобщённых формул трапеции и Симпсона.
- •16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.
- •17. Общие свойства полиномов ортогональных с весом.
- •18. Алгебраическая степень точности квадратурной формулы. Квадратурные формулы Гаусса-Кристоффеля.
- •19. Теорема о необходимых и достаточных условиях выбора узлов в формулах Гаусса-Кристоффеля.
- •21. Принцип сжатых отображений. Теорема о неподвижной точке. Доказать единственность неподвижной точки. Следствия теоремы для банаховых пространств и пространства
- •22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.
- •23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.
- •24. Метод Ньютона в многомерном случае. Организация итерационного алгоритма.
- •25. Численные методы решения слау. Прямые и итерационные методы, общие понятия.
- •26. Нормы вещественных квадратных матриц. Спектральные свойства матриц.
- •27. Обусловленность матриц и систем лау. Число обусловленности в спектральной норме.
- •28. Метод итераций для слау специального вида. Теорема о достаточных условия сходимости.
- •29. Спектральный признак сходимости.(теорема о необх. И дост. Усл. Сходимости)
- •30.Стационарные итерационные процедуры. Приведение слау к системе специального вида.
- •31. Метод простых итераций Ричардсона. Условия сходимости.
- •32. Теорема о выборе ускоряющего множителя в методе Ричардсона.
- •33. Метод Якоби. Организация алгоритма. Теорема о достаточных условиях сходимости.
- •34. Метод Зейделя как ускорение метода Якоби. Организация алгоритма. Теорема об условиях сходимости.
- •35. Метод последовательной верхней релаксации. Задача выбора ускоряющего множителя.
- •36. Численное дифференцирование на основе интерполяции.
- •37. Численное дифференцирование на равномерной сетке, основанное на тэйлоровском разложении. Теорема об аппроксимации первой и второй производной.
- •38. Задача Коши. Постановка задачи. Сведение к системе для уравнения n-ого порядка.
- •39. Метод Эйлера. Алгоритм, геометрическая интерпретация, порядок точности.
- •40. Методы Рунге-Кутты повышенной точности. Метод «предиктор-корректор» и метод «средней точки».
- •41. Общая постановка краевой задачи для решения оду второго порядка. Классификация граничных условий.
- •42. Метод «стрельбы» решения краевой задачи с граничными условиями первого рода.
- •43. Метод конечных разностей решения линейной краевой задачи для оду второго порядка.
- •44. Каноническая разностная схема для линейного оду второго порядка, имеющая порядок аппроксимации .
- •45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.
36. Численное дифференцирование на основе интерполяции.
Если функция
![]() задана таблично, то аналитическое
дифференцирование невозможно. Строится
интерполяционный полином и его производную
принимают приближенно за
задана таблично, то аналитическое
дифференцирование невозможно. Строится
интерполяционный полином и его производную
принимают приближенно за
![]() .
.
Запишем 1-ую форму интерполяционного полинома Ньютона на равномерной сетке:
|
(1) |
где
![]()
 .
.
![]() - погрешность
интерполяции.
- погрешность
интерполяции.
Дифференцируя (1), получим:
 ,
,
где
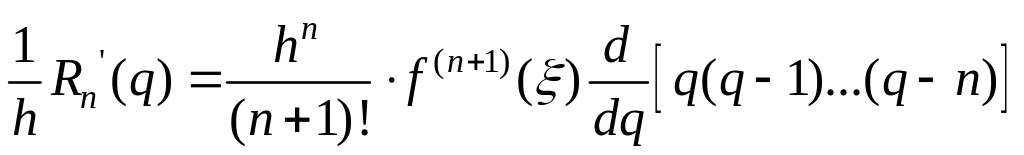 -
-
- теоретическая погрешность производной.
Пример 1.
Пусть
![]() .
Вычислить приближенно первую производную
.
Вычислить приближенно первую производную
![]() и оценить погрешность (теоретическую).
и оценить погрешность (теоретическую).
На данной сетке
получаем:
![]() .
.
Интерполяционный полином третьего порядка имеет вид:
![]() ;
;
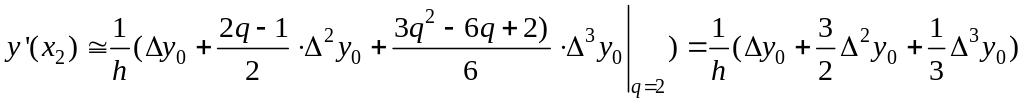 ;
;
 .
.
37. Численное дифференцирование на равномерной сетке, основанное на тэйлоровском разложении. Теорема об аппроксимации первой и второй производной.
Пусть задана сетка
![]() .
.
Теорема 4.1.
Обозначим
![]() и т.д. и пусть
и т.д. и пусть
![]() ,
тогда существует такая точка
,
тогда существует такая точка
![]() ,
для которой справедлива формула:
,
для которой справедлива формула:
|
(2) |
Т.к.
,
то справедливо разложение Тейлора с
центром в точке
![]() и остаточным членом в форме Лагранжа:
и остаточным членом в форме Лагранжа:
![]() .
.
В точке
![]() получаем:
получаем:
![]() ,
откуда следует
,
откуда следует
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Теорема 4.2. Пусть
![]() тогда
тогда![]() .
(3)
.
(3)
Самостоятельно. См. ход доказательства следующей теоремы .
Теорема 4.3. Пусть
![]() ,
тогда существует такая точка
,
тогда существует такая точка
![]() ,
что справедлива формула
,
что справедлива формула
|
(4) |
По условию теоремы
справедливо тейлоровское разложение
функции
с центром в точке
:![]() ,
(5)
,
(5)
где
![]() .
Положим в формуле (5) последовательно
.
Положим в формуле (5) последовательно
![]() и
и
![]() :
:
![]()
Складывая эти две формулы, получим
![]() .
.
В силу непрерывности
четвертой производной
![]() :
:
![]() ,
,
Откуда следует:
![]() ,
т.е. формула (4)
.
,
т.е. формула (4)
.
Замечание. Формулы
(2), (3) и (4) называются формулами
численного дифференцирования.
При этом формула (2) аппроксимирует
первую производную в узле
правой
конечной разностью
и имеет порядок
точности
![]() (т.е.
первый
порядок);
(т.е.
первый
порядок);
формула (3)
аппроксимирует первую производную
центральной конечной разностью и имеет
порядок
точности
![]() (второй
порядок);
формула (4) аппроксимирует вторую
производную в узле
центральной конечной разностью и имеет
порядок
точности
.
(второй
порядок);
формула (4) аппроксимирует вторую
производную в узле
центральной конечной разностью и имеет
порядок
точности
.
38. Задача Коши. Постановка задачи. Сведение к системе для уравнения n-ого порядка.
Задача Коши для ОДУ первого порядка для функции одной переменной ставится следующим образом:
|
(6) |
Более общая постановка задачи Коши для дифференциального уравнения n-го порядка:
|
(7) |
Здесь
![]() - заданные числа (начальные условия).
- заданные числа (начальные условия).
Задача (7) с помощью замены переменных
![]() ,
,
![]()
сводится к системе дифференциальных уравнений первого порядка:
|
(8) |
Систему (8) можно переписать в векторном виде:
|
(9) |
где
![]() ,
,
![]() ,
,
![]() .
.
Система (9) исследуется и решается аналогично одномерной задаче Коши (6), поэтому важно изучить, прежде всего, численные методы решения задачи (6).
В курсе математического
анализа формулируется и доказывается
теорема существования и единственности
решения задачи Коши. Отметим, что для
выполнения теоремы необходимо и
достаточно, чтобы функция
![]() имела непрерывные частные производные
по
имела непрерывные частные производные
по
![]() в замкнутой ограниченной области
в замкнутой ограниченной области
![]() на плоскости
на плоскости
![]() .
.