
- •2. Позиционная и нормализованная формы записи чисел. Значащие и верные цифры позиционной системы.
- •3. Ошибки округления чисел. Распространение ошибок округления в арифметических операциях. Абсолютная и относительная погрешность суммы, разности, произведения и частного.
- •Определение 2. Величина называется абсолютной погрешностью представления числа X с помощью числа .
- •4. Близость в метрическом и нормированном пространствах. Расстояние и норма, их определения и свойства. Основные классы функций:
- •5. Постановка задачи интерполяции. Интерполяционный многочлен Лагранжа. Теорема о погрешности интерполяции. Единственность многочлена Лагранжа.
- •6. Интерполяция на равномерной сетке. Конечные разности и их свойства.
- •1) Докажем, что операторы и перестановочные. .
- •7. Интерполяционный многочлен Ньютона. Построение и оценка погрешности.
- •8. Ортогональность в гильбертовом пространстве. Многочлены Чебышёва. Определение, построение, свойства.
- •9. Применение многочленов Чебышёва к задаче интерполяции. Теорема об оптимальном выборе узлов.
- •10. Среднеквадратичное приближение функций. Постановка задачи, теорема о существовании и единственности.
- •20. Классические ортогональные многочлены. Построение ортогональных многочленов на каноническом отрезке [-1,1].
- •11. Численное интегрирование. Использование функциональных рядов.
- •12. Квадратурная формула на основе интерполяции. Формулы дл коэффициентов и остаточного члена.
- •13. Базовые квадратурные формулы прямоугольников, трапеций и парабол. Формула теоретической погрешности.
- •14. Обобщенные квадратурные формулы трапеции и Симпсона (формулы Ньютона-Котеса).
- •15. Теоретич. Оценки погрешности обобщённых формул трапеции и Симпсона.
- •16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.
- •17. Общие свойства полиномов ортогональных с весом.
- •18. Алгебраическая степень точности квадратурной формулы. Квадратурные формулы Гаусса-Кристоффеля.
- •19. Теорема о необходимых и достаточных условиях выбора узлов в формулах Гаусса-Кристоффеля.
- •21. Принцип сжатых отображений. Теорема о неподвижной точке. Доказать единственность неподвижной точки. Следствия теоремы для банаховых пространств и пространства
- •22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.
- •23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.
- •24. Метод Ньютона в многомерном случае. Организация итерационного алгоритма.
- •25. Численные методы решения слау. Прямые и итерационные методы, общие понятия.
- •26. Нормы вещественных квадратных матриц. Спектральные свойства матриц.
- •27. Обусловленность матриц и систем лау. Число обусловленности в спектральной норме.
- •28. Метод итераций для слау специального вида. Теорема о достаточных условия сходимости.
- •29. Спектральный признак сходимости.(теорема о необх. И дост. Усл. Сходимости)
- •30.Стационарные итерационные процедуры. Приведение слау к системе специального вида.
- •31. Метод простых итераций Ричардсона. Условия сходимости.
- •32. Теорема о выборе ускоряющего множителя в методе Ричардсона.
- •33. Метод Якоби. Организация алгоритма. Теорема о достаточных условиях сходимости.
- •34. Метод Зейделя как ускорение метода Якоби. Организация алгоритма. Теорема об условиях сходимости.
- •35. Метод последовательной верхней релаксации. Задача выбора ускоряющего множителя.
- •36. Численное дифференцирование на основе интерполяции.
- •37. Численное дифференцирование на равномерной сетке, основанное на тэйлоровском разложении. Теорема об аппроксимации первой и второй производной.
- •38. Задача Коши. Постановка задачи. Сведение к системе для уравнения n-ого порядка.
- •39. Метод Эйлера. Алгоритм, геометрическая интерпретация, порядок точности.
- •40. Методы Рунге-Кутты повышенной точности. Метод «предиктор-корректор» и метод «средней точки».
- •41. Общая постановка краевой задачи для решения оду второго порядка. Классификация граничных условий.
- •42. Метод «стрельбы» решения краевой задачи с граничными условиями первого рода.
- •43. Метод конечных разностей решения линейной краевой задачи для оду второго порядка.
- •44. Каноническая разностная схема для линейного оду второго порядка, имеющая порядок аппроксимации .
- •45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.
24. Метод Ньютона в многомерном случае. Организация итерационного алгоритма.
Пусть задана
система нелинейных уравнений
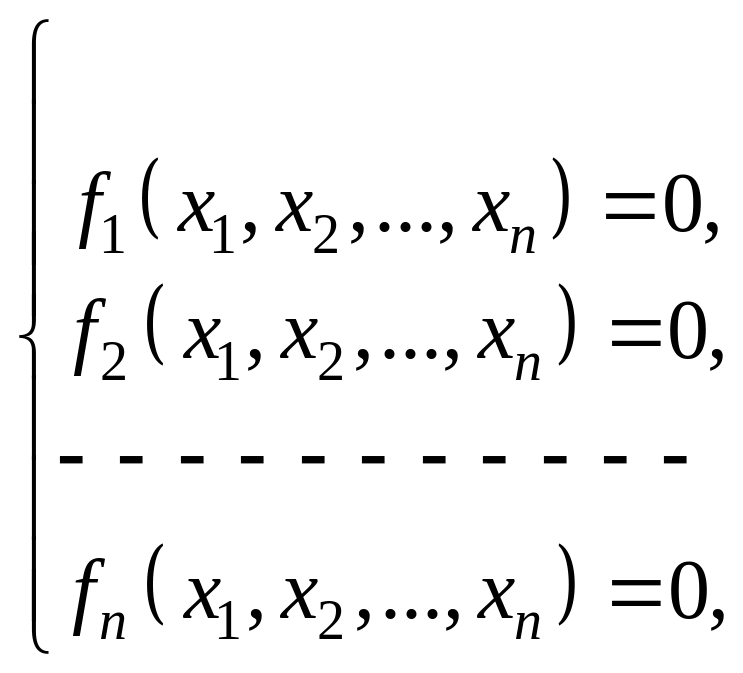
или в более
компактной форме: f(x)=0,
где
![]() ─
-мерная
вектор-функция (вектор-столбец). Для
реализации метода решения и исследования
сходимости необходимо, чтобы функции
─
-мерная
вектор-функция (вектор-столбец). Для
реализации метода решения и исследования
сходимости необходимо, чтобы функции
![]() были достаточно гладкими, например,
были достаточно гладкими, например,
![]() ,
где
,
где
![]() .
Рассмотрим i-ое
уравнение системы:
.
Рассмотрим i-ое
уравнение системы:
![]() и
пусть
и
пусть
![]() - некоторое приближение к корню
- некоторое приближение к корню
![]() ,
полученное на k-ой
итерации. Разложим функцию
в многомерный ряд Тейлора в точке
:
,
полученное на k-ой
итерации. Разложим функцию
в многомерный ряд Тейлора в точке
:
|
(17) |
где
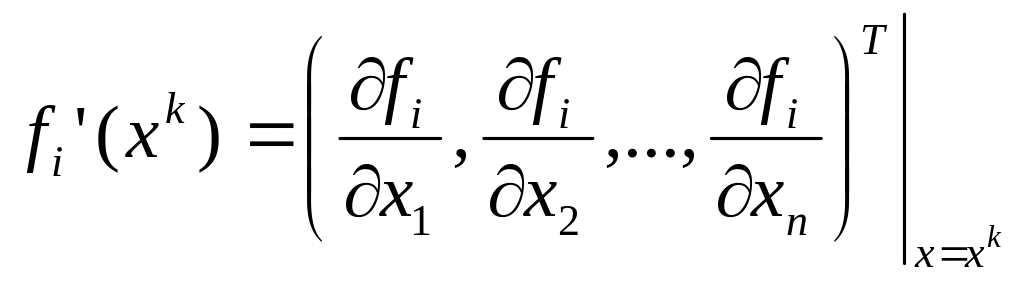 -
-
- вектор-градиент
функции
в точке
,
а
![]() - скалярное произведение векторов a
и b.
Пренебрегая остаточным членом в (17),
положим
- скалярное произведение векторов a
и b.
Пренебрегая остаточным членом в (17),
положим
![]()
или в более компактной матричной форме:
|
(18) |
где
 -
-
- так называемая матрица Якоби первых производных в точке .
Пусть
![]() .
Разрешим систему линейных алгебраических
уравнений (18) относительно x:
.
Разрешим систему линейных алгебраических
уравнений (18) относительно x:
![]()
И положим
![]() :
:
|
(19) |
Векторное уравнение
(19) представляет собой итерационную
процедуру Ньютона в многомерном случае.
Для ее запуска необходимо задать
начальную точку
![]() .
Однако при произвольном выборе начальной
точки нельзя гарантировать сходимость
процедуры Ньютона. Вопрос о сходимости
(19) в теоретическом плане более сложный,
чем тот же вопрос о сходимости метода
Ньютона в одномерном случае. Рассмотрим
некоторые основные моменты проблемы
исследования сходимости процедуры
(19).
.
Однако при произвольном выборе начальной
точки нельзя гарантировать сходимость
процедуры Ньютона. Вопрос о сходимости
(19) в теоретическом плане более сложный,
чем тот же вопрос о сходимости метода
Ньютона в одномерном случае. Рассмотрим
некоторые основные моменты проблемы
исследования сходимости процедуры
(19).
Прежде всего
отметим, что для реализации метода
Ньютона необходимо, чтобы матрица Якоби
![]() была невырождена в некоторой окрестности
точки
была невырождена в некоторой окрестности
точки
![]() .
Тогда обратная матрица
.
Тогда обратная матрица
![]() существует в этой окрестности. Аналогично
одномерному случаю, процедуру (19) можно
рассматривать как итерационный поиск
неподвижной точки для уравнения
существует в этой окрестности. Аналогично
одномерному случаю, процедуру (19) можно
рассматривать как итерационный поиск
неподвижной точки для уравнения
![]() ,
где
-
-мерная
оператор-функция.
Можно показать, что
.
Поэтому, как и в одномерном случае
существует окрестность точки
,
в которой оператор-функция
является сжимающим оператором с некоторой
константой сжатия
,
где
-
-мерная
оператор-функция.
Можно показать, что
.
Поэтому, как и в одномерном случае
существует окрестность точки
,
в которой оператор-функция
является сжимающим оператором с некоторой
константой сжатия
![]() ,
тем меньшей, чем ближе точка
,
тем меньшей, чем ближе точка
![]() к точке
(в эвклидовой норме).
к точке
(в эвклидовой норме).
Поэтому о характере сходимости многомерного метода Ньютона справедливы утверждения, аналогичные одномерному случаю.
Например, если
- строго выпукла в G,
![]() и начальное приближение
и начальное приближение
![]() выбирается достаточно близко к
выбирается достаточно близко к
![]() ,
то итерационная процедура Ньютона (19)
сходится с линейной скоростью, а, начиная
с некоторого номера, - и с квадратичной
скоростью.
,
то итерационная процедура Ньютона (19)
сходится с линейной скоростью, а, начиная
с некоторого номера, - и с квадратичной
скоростью.
Замечание. Строгую
формулировку достаточных условий
сходимости метода Ньютона в многомерном
случае можно найти в цитируемой литературе
(см., например, [2]). На практике эти условия,
как правило, проверить чрезвычайно
сложно. Поэтому при работе на компьютере
(например, в пакете MATLAB)
используют метод
проб и ошибок
при выборе начальной точки
![]() .
На начальном этапе важно найти так
называемую зону
притяжения,
т.е. такую область
.
На начальном этапе важно найти так
называемую зону
притяжения,
т.е. такую область
![]() ,
что при выборе
,
что при выборе
![]() процедура (19) сходится.
процедура (19) сходится.
25. Численные методы решения слау. Прямые и итерационные методы, общие понятия.
Пусть задана система линейных алгебраических уравнений (ЛАУ) в стандартной форме:
![]() ,
,
где
![]() - матрица
- матрица
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Если
![]() - то решение системы существует и
единственно.
- то решение системы существует и
единственно.
Формальное решение системы можно записать по известным формулам Крамера
![]() ,
,
где определители
![]() вычисляются по известному правилу.
вычисляются по известному правилу.
Однако с вычислительной
точки зрения формальное решение не
эффективно (хотя и устойчиво) – требует
слишком много операций на вычисление
определителей (для каждого определителя
![]() слагаемых). Это совершенно неприемлемо
даже для современных компьютеров уже
при
слагаемых). Это совершенно неприемлемо
даже для современных компьютеров уже
при
![]() .
Поэтому используются другие методы
численного решения. Эти методы делятся
на две большие группы: 1)– прямые методы
и 2) – итерационные методы.
.
Поэтому используются другие методы
численного решения. Эти методы делятся
на две большие группы: 1)– прямые методы
и 2) – итерационные методы.
Прямые методы
основаны на последовательном исключении
неизвестных и приведении матрицы A
к треугольному виду (метод Гаусса и его
модификации, основанные на определенном
правиле
выбора главного элемента).
Эти методы дают решение СЛАУ за конечное
число арифметических операций – это
их основное преимущество. Число операций,
затрачиваемых на приведение системы к
треугольному виду и последующее решение
пропорционально
![]() .
Основной недостаток прямых методов –
возможно сильное накопление ошибок
округлений при делении на малые числа.
Кроме того, возможно возникновение так
называемой неустранимой погрешности,
если система (и соответственно матрица
)
плохо
обусловлена.
Это свойство систем обсуждается далее
в п.п.3.4.2.
.
Основной недостаток прямых методов –
возможно сильное накопление ошибок
округлений при делении на малые числа.
Кроме того, возможно возникновение так
называемой неустранимой погрешности,
если система (и соответственно матрица
)
плохо
обусловлена.
Это свойство систем обсуждается далее
в п.п.3.4.2.
Итерационные
методы более
эффективны в вычислении и применяются
для разреженных (слабо заполненных)
систем порядка
![]() и более.
и более.
Метод Гаусса обычно изучается в курсе линейной алгебры, и мы его рассматривать не будем. Более подробно рассмотрим итерационные методы. Для тех или иных оценок решения понадобится понятие нормы вектора и нормы матрицы, которые мы и обсудим в следующем параграфе.
