
- •2. Позиционная и нормализованная формы записи чисел. Значащие и верные цифры позиционной системы.
- •3. Ошибки округления чисел. Распространение ошибок округления в арифметических операциях. Абсолютная и относительная погрешность суммы, разности, произведения и частного.
- •Определение 2. Величина называется абсолютной погрешностью представления числа X с помощью числа .
- •4. Близость в метрическом и нормированном пространствах. Расстояние и норма, их определения и свойства. Основные классы функций:
- •5. Постановка задачи интерполяции. Интерполяционный многочлен Лагранжа. Теорема о погрешности интерполяции. Единственность многочлена Лагранжа.
- •6. Интерполяция на равномерной сетке. Конечные разности и их свойства.
- •1) Докажем, что операторы и перестановочные. .
- •7. Интерполяционный многочлен Ньютона. Построение и оценка погрешности.
- •8. Ортогональность в гильбертовом пространстве. Многочлены Чебышёва. Определение, построение, свойства.
- •9. Применение многочленов Чебышёва к задаче интерполяции. Теорема об оптимальном выборе узлов.
- •10. Среднеквадратичное приближение функций. Постановка задачи, теорема о существовании и единственности.
- •20. Классические ортогональные многочлены. Построение ортогональных многочленов на каноническом отрезке [-1,1].
- •11. Численное интегрирование. Использование функциональных рядов.
- •12. Квадратурная формула на основе интерполяции. Формулы дл коэффициентов и остаточного члена.
- •13. Базовые квадратурные формулы прямоугольников, трапеций и парабол. Формула теоретической погрешности.
- •14. Обобщенные квадратурные формулы трапеции и Симпсона (формулы Ньютона-Котеса).
- •15. Теоретич. Оценки погрешности обобщённых формул трапеции и Симпсона.
- •16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.
- •17. Общие свойства полиномов ортогональных с весом.
- •18. Алгебраическая степень точности квадратурной формулы. Квадратурные формулы Гаусса-Кристоффеля.
- •19. Теорема о необходимых и достаточных условиях выбора узлов в формулах Гаусса-Кристоффеля.
- •21. Принцип сжатых отображений. Теорема о неподвижной точке. Доказать единственность неподвижной точки. Следствия теоремы для банаховых пространств и пространства
- •22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.
- •23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.
- •24. Метод Ньютона в многомерном случае. Организация итерационного алгоритма.
- •25. Численные методы решения слау. Прямые и итерационные методы, общие понятия.
- •26. Нормы вещественных квадратных матриц. Спектральные свойства матриц.
- •27. Обусловленность матриц и систем лау. Число обусловленности в спектральной норме.
- •28. Метод итераций для слау специального вида. Теорема о достаточных условия сходимости.
- •29. Спектральный признак сходимости.(теорема о необх. И дост. Усл. Сходимости)
- •30.Стационарные итерационные процедуры. Приведение слау к системе специального вида.
- •31. Метод простых итераций Ричардсона. Условия сходимости.
- •32. Теорема о выборе ускоряющего множителя в методе Ричардсона.
- •33. Метод Якоби. Организация алгоритма. Теорема о достаточных условиях сходимости.
- •34. Метод Зейделя как ускорение метода Якоби. Организация алгоритма. Теорема об условиях сходимости.
- •35. Метод последовательной верхней релаксации. Задача выбора ускоряющего множителя.
- •36. Численное дифференцирование на основе интерполяции.
- •37. Численное дифференцирование на равномерной сетке, основанное на тэйлоровском разложении. Теорема об аппроксимации первой и второй производной.
- •38. Задача Коши. Постановка задачи. Сведение к системе для уравнения n-ого порядка.
- •39. Метод Эйлера. Алгоритм, геометрическая интерпретация, порядок точности.
- •40. Методы Рунге-Кутты повышенной точности. Метод «предиктор-корректор» и метод «средней точки».
- •41. Общая постановка краевой задачи для решения оду второго порядка. Классификация граничных условий.
- •42. Метод «стрельбы» решения краевой задачи с граничными условиями первого рода.
- •43. Метод конечных разностей решения линейной краевой задачи для оду второго порядка.
- •44. Каноническая разностная схема для линейного оду второго порядка, имеющая порядок аппроксимации .
- •45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.
22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.
Пусть
![]() (одномерный
случай) и задана функция f(x),
удовлетворяющая условиям:
(одномерный
случай) и задана функция f(x),
удовлетворяющая условиям:
1)
условие Липшица
с константой
2) . |
(1) |
Тогда оператор f(x) - сжимающий и уравнение f(x)=х имеет единственную неподвижную точку, которую можно найти методом простых итераций:
![]() .
.
Действительно,
определим
![]() .
Следовательно, выполняется условие
Липшица из теоремы 3.2, откуда и следует
результат.
.
Следовательно, выполняется условие
Липшица из теоремы 3.2, откуда и следует
результат.
Теорема 3.4. Пусть , причем выполнены условия:
1) ; 2) |
(8) |
Тогда оператор f(x) является сжимающим, и справедливо утверждение теоремы 3.1, т.е. последовательность сходится к единственному коню уравнения .
Пусть , тогда , согласно условию 1) теоремы. Далее по индукции устанавливаем, что все члены последовательности принадлежат . Пусть . Согласно теореме о среднем
, . Оценим это неравенство по модулю:
согласно условию 2) теоремы.
Таким образом, выполняются все условия теоремы 3.3., откуда и следует результат.
Рассмотрим задачу
поиска корней уравнения
![]() .
Пусть известны границы для единственного
корня этого уравнения и мы хотим найти
этот корень методом итераций. Если
удастся привести уравнение к виду
x=f(x),
так чтобы
выполнялись условия теоремы 3.3 или
теоремы 3.4, то в этом случае можно будет
применить метод итераций. Такое
преобразование, вообще говоря, не
единственно, причем главная трудность
заключается в определении того замкнутого
ограниченного множества S
(а в одномерном случае – отрезка [a,b]),
для которого помимо условия сжатости,
выполняется условие
.
Пусть известны границы для единственного
корня этого уравнения и мы хотим найти
этот корень методом итераций. Если
удастся привести уравнение к виду
x=f(x),
так чтобы
выполнялись условия теоремы 3.3 или
теоремы 3.4, то в этом случае можно будет
применить метод итераций. Такое
преобразование, вообще говоря, не
единственно, причем главная трудность
заключается в определении того замкнутого
ограниченного множества S
(а в одномерном случае – отрезка [a,b]),
для которого помимо условия сжатости,
выполняется условие
![]() .
.
Лемма 3.1. Определим
множество
![]() -
замкнутый r-“шар”
с центром в точке х0
(в одномерном случае – отрезок). Пусть
оператор Т
- сжимающий на S
и выполняется следующее условие:
-
замкнутый r-“шар”
с центром в точке х0
(в одномерном случае – отрезок). Пусть
оператор Т
- сжимающий на S
и выполняется следующее условие:
|
(9) |
Тогда для любой
точки
![]() выполняется:
выполняется:
![]() .
.
Достаточно
доказать, что
![]() Имеем:
Имеем:
![]() {неравенство
треугольника}
{неравенство
треугольника}
![]() .
.
23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.
Пусть снова задано
уравнение f(x)=0.
Запишем его в виде
![]() ,
,
где
![]() положим
положим
![]() .
Пусть хк
– некоторое приближение к корню х*.
Для ускорения сходимости итераций
желательно, чтобы
.
Пусть хк
– некоторое приближение к корню х*.
Для ускорения сходимости итераций
желательно, чтобы
![]() был как можно меньше. Положим
был как можно меньше. Положим
![]() Отсюда
находим, что
Отсюда
находим, что
 .
Подставляя в исходное уравнение, получаем
рекуррентную формулу:
.
Подставляя в исходное уравнение, получаем
рекуррентную формулу:
 ,
(11)
,
(11)
Это и есть итерационная процедура Ньютона.
Метод Ньютона
известен и под другим названием: метод
касательных.
Дадим графическую иллюстрацию данного
метода. Пусть
и строго выпукла (т.е.
![]() ).
Пусть, кроме того,
- единственный корень функции
на промежутке
.
).
Пусть, кроме того,
- единственный корень функции
на промежутке
.
В качестве начального
приближения возьмем точку
![]() ,
такую, для которой
,
такую, для которой
![]() .
Проведем через точку на плоскости
.
Проведем через точку на плоскости
![]() касательную к кривой
касательную к кривой
![]() .
Запишем уравнение касательной:
.
Запишем уравнение касательной:
![]() .
В качестве следующего приближения
возьмем точку
.
В качестве следующего приближения
возьмем точку
![]() ,
в которой
,
в которой
![]()
![]() .
Отсюда находим
.
Отсюда находим
![]() .
Далее в точке графика
.
Далее в точке графика
![]() проводим новую касательную, и т.д. В
результате получаем итерационную
процедуру Ньютона (11).
проводим новую касательную, и т.д. В
результате получаем итерационную
процедуру Ньютона (11).
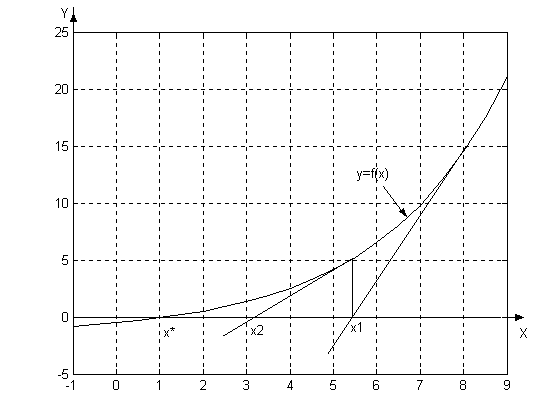
Метод касательных проиллюстрирован на рис.3.2.
Рис.3.2. Графическая иллюстрация метода Ньютона (метода касательных).
Начальная точка x0 = 8. Точное значение корня x* = 1. x1 и x2 – два последовательных приближения к корню, полученные с помощью касательных.
Исследуем условия сходимости метода Ньютона.
Теорема 3.5. Пусть
![]() ,
,
![]() на
,
и
имеет единственный действительный
корень на
.
Тогда
на
,
и
имеет единственный действительный
корень на
.
Тогда
![]() ,
такое, что на множестве
,
такое, что на множестве
![]()
процедура Ньютона (1) сходится к точке со скоростью геометрической прогрессии, а в некоторой малой окрестности точки x* и с квадратичной скоростью.
В силу непрерывности
функций
![]() на [a,b],
обе производные ограничены поэтому
на [a,b],
обе производные ограничены поэтому
![]() ,
причем
,
причем
![]() по условию.
по условию.
Заметим, что
итерационная процедура (11) равносильна
методу простых итераций для уравнения
 (12)
(12)
Очевидно, что
является неподвижной точкой функционального
оператора
![]() ,
называемого операторной
функцией Ньютона-Рафсона.
Проверим условия сжатости данной
функции. Для этого вычислим и оценим
производную
,
называемого операторной
функцией Ньютона-Рафсона.
Проверим условия сжатости данной
функции. Для этого вычислим и оценим
производную
![]() .
Имеем:
.
Имеем:
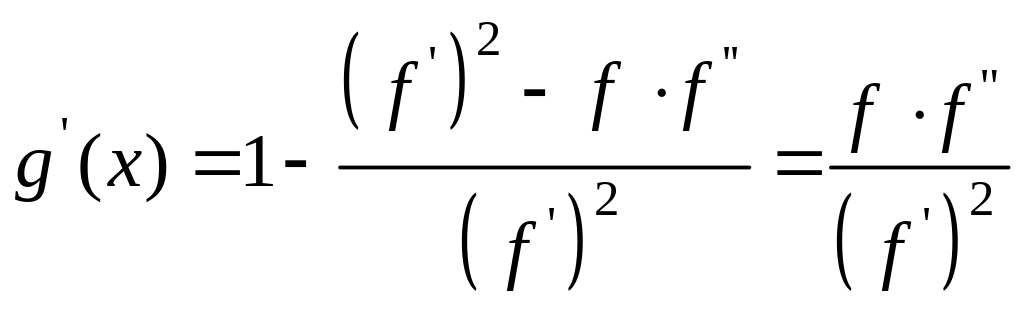 .
.
Оценивая полученное
равенство по модулю, и учитывая условия
теоремы, получим
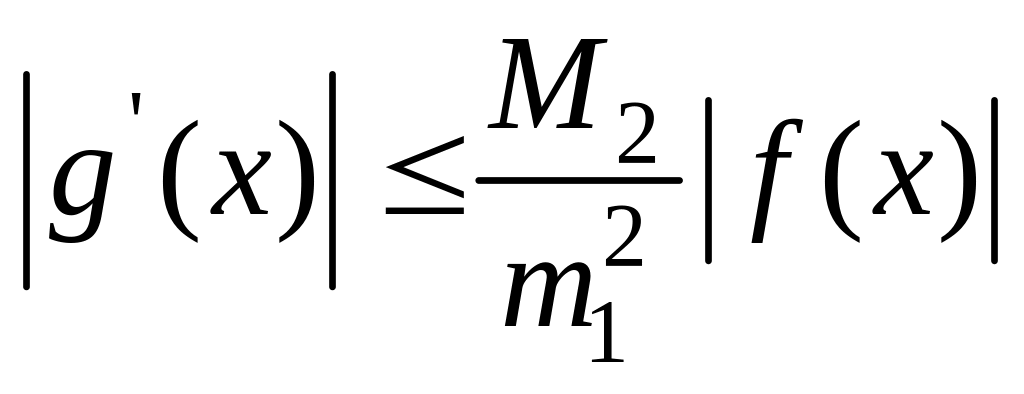 (13) Поскольку
- корень уравнения
(13) Поскольку
- корень уравнения
![]() ,
то, как следует из неравенства (13),
,
то, как следует из неравенства (13),
![]() и близка к нулю в некоторой малой
окрестности точки
,
где и следует ожидать выполнения условия
сжатости. Запишем формулу конечных
приращений Лагранжа
и близка к нулю в некоторой малой
окрестности точки
,
где и следует ожидать выполнения условия
сжатости. Запишем формулу конечных
приращений Лагранжа ![]() .
.
Оценивая по модулю,
получаем
![]() .
.
Подставляя эту
оценку в (13), получаем:
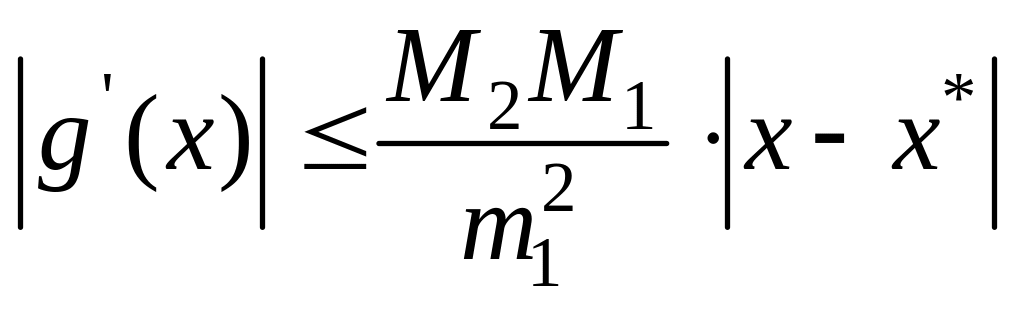 .
.
Условие сжатости
![]() будет, очевидно, выполнено, если
будет, очевидно, выполнено, если
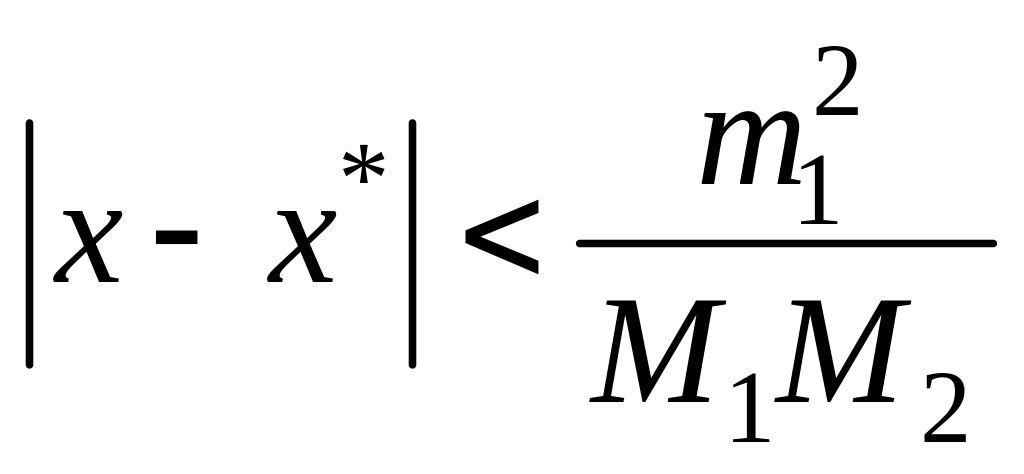 .
(14)
.
(14)
Обозначив
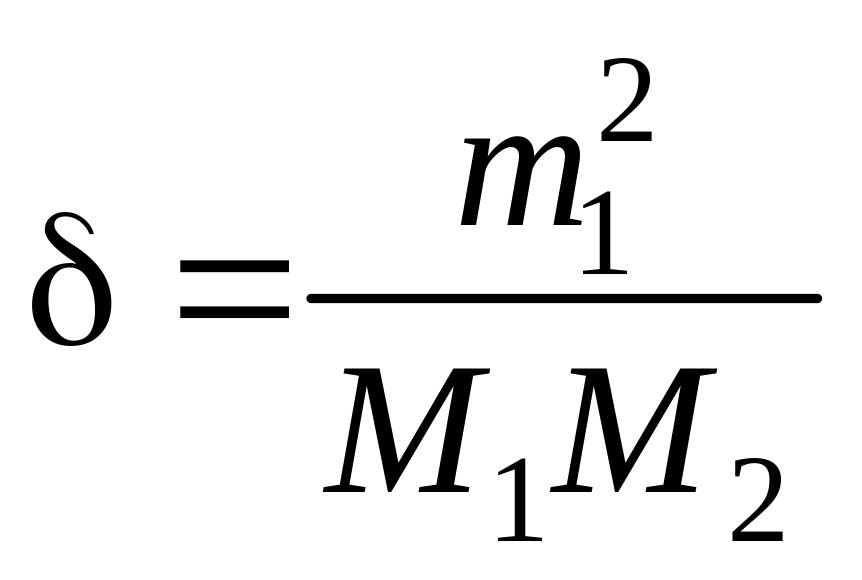 ,
получаем конкретизацию окрестности
,
получаем конкретизацию окрестности
![]() ,
где выполняется одно из условий сжатости.
Пусть теперь найдено
,
где выполняется одно из условий сжатости.
Пусть теперь найдено
![]() -е
приближение к корню
-е
приближение к корню
![]() .
.
Так как по условию
теоремы
![]() непрерывна на
,
то справедливо тэйлоровское разложение
функции
с центром в точке
непрерывна на
,
то справедливо тэйлоровское разложение
функции
с центром в точке
![]() с остаточным членом в форме Лагранжа
с остаточным членом в форме Лагранжа
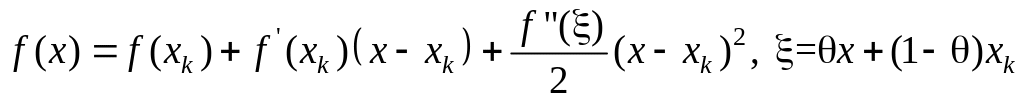
Положим в последнем
равенстве
![]() :
:
![]() .
.
Выражая отсюда
,
получим:
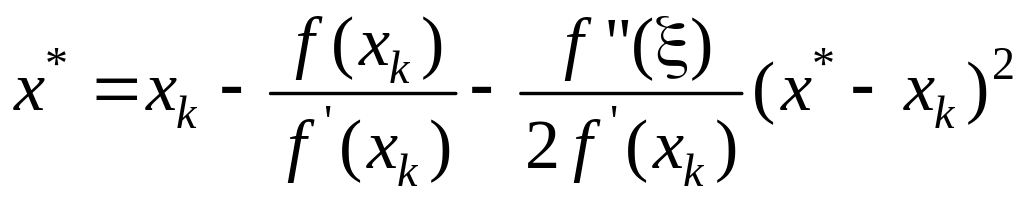 (15)
(15)
Вычтем (15) из (11):
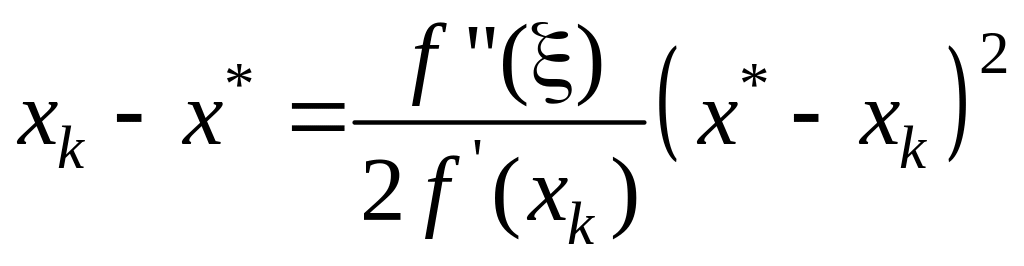 ;
;
Оценивая последнее
равенство по модулю, получаем: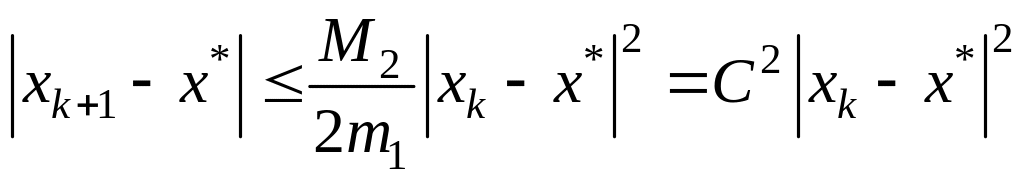 (16)
(16)
Продолжим далее оценку по модулю, используя (14):
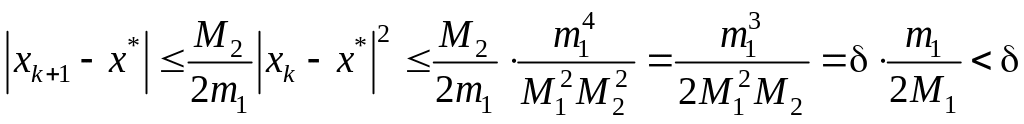 .
.
Таким образом,
если
,
где
![]() определяется из неравенства (14), то точка
определяется из неравенства (14), то точка
![]() .
Следовательно, выполняется и второе
условие теоремы 3.4, а значит последовательность
.
Следовательно, выполняется и второе
условие теоремы 3.4, а значит последовательность
![]() сходится к корню
со скоростью геометрической
последовательности (т.е. линейно). Далее
из неравенства (16) следует, что как только
при некотором
сходится к корню
со скоростью геометрической
последовательности (т.е. линейно). Далее
из неравенства (16) следует, что как только
при некотором
![]() выполнится условие
выполнится условие
![]() ,
так в дальнейшем, при
,
так в дальнейшем, при
![]() сходимость становится квадратичной:
сходимость становится квадратичной:
![]() .
.
