
- •Лабораторная работа №14
- •I. Краткие теоретические сведения.
- •1.2. Уравнения, допускающие понижение порядка.
- •1.3. Линейные дифференциальные уравнения высших порядков.
- •1.3.1. Структура общего решения однородного линейного дифференциального уравнения.
- •1.3.2. Структура общего решения линейного дифференциального уравнения.
- •1.3.3. Общее решение однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
- •Случай комплексно-сопряженных корней.
- •1.3.4. Решение олду более высоких порядков.
- •1.3.5. Решение нлду с постоянными коэффициентами.
- •I. Метод вариации.
- •II. Нахождение частного решения нлду по виду правой части.
- •II. Примеры решения заданий практической части.
- •Найти частное решение дифференциального уравнения (решить задачу Коши).
- •2. Найти общее решение дифференциального уравнения, допускающего понижение порядка.
- •Определить и записать структуру частного решения линейного неоднородного дифференциального уравнения по виду функции f(X).
- •4. Найти общее решение линейного неоднородного дифференциального уравнения.
- •5. Найти частное решение линейного неоднородного дифференциального уравнения, удовлетворяющее данным начальным условиям (решить задачу Коши).
- •6. Решить дифференциальное уравнение методом вариации произвольной постоянной (методом Лагранжа).
- •III. Задания для практической части.
- •1. Найти частное решение дифференциального уравнения (решить задачу Коши).
- •2. Найти общее решение дифференциального уравнения, допускающего понижение порядка.
- •3. Найти общее решение линейного однородного дифференциального уравнения.
Пусть f(x)=ex (Pn(x)cosx+Qm(x)sinx), где Pn(x) – многочлен n-ой степени от х, Qm(x) –многочлен m-ой степени от х, – некоторое число.
Возможны два случая:
(+i) не является корнем характеристического уравнения, тогда частное решение имеет вид: учн= ex(Rp(x)cosx+Kp(x)sinx), где Rp(x), Kp(x)– многочлены степени р от х, причем p=max(n,m);
(+i) является корнем характеристического уравнения кратности s, тогда частное решение имеет вид: учн= exxs(Rp(x)cosx+Kp(x)sinx), где Rp(x), Kp(x)– многочлены степени р от х, причем p=max(n,m).
Пример.
Решить НЛДУ второго порядка: y-3y+2y=(x2+х)е3х.
Найдем общее решение соответствующего ОЛДУ y-3y+2y=0. составим и решим характеристическое уравнение: к2-3к+2=0, к1=2, к2=1. Тогда уоо=С1е2х+С2ех.
Найдем частное решение данного НЛДУ. Функция f(x)=(x2+х)е3х является функцией специального вида f(x)=exPn(x), при Pn(x)= x2+х – многочлен второй степени от х, =3 не является корнем характеристического уравнения, поэтому частное решение будем искать в виде учн=(Ах2+Вx+С)e3x. Найдем значения неопределенных коэффициентов А, В, С.
учн=(2Ах+В)e3x+3(Ах2+Вx+С)e3x= e3x(3Ах2+(2А+3В)х+В+3С);
учн=(6Ах+2А+3В)e3x+3(3Ах2+(2А+3В)х+В+3С)e3x= e3x(9Ах2+(12А+9В)х+2А+6В+9С).
Подставим полученные значения в уравнение:
e3x(9Ах2+(12А+9В)х+2А+6В+9С)-3e3x(3Ах2+(2А+3В)х+В+3С)+2(Ах2+Вx+С)e3x=(x2+х)е3х;
9Ах2+(12А+9В)х+2А+6В+9С-9Ах2-(6А+9В)х-3В-9С+2Ах2+2Вx+2С= x2+х;
2Ах2+(6А+2В)х+2А+3В+2С=x2+х;
так как многочлены, стоящие в левой и правой частях уравнения, равны при любых значениях переменной, то коэффициенты при соответствующих степенях х также должны быть равны; тогда
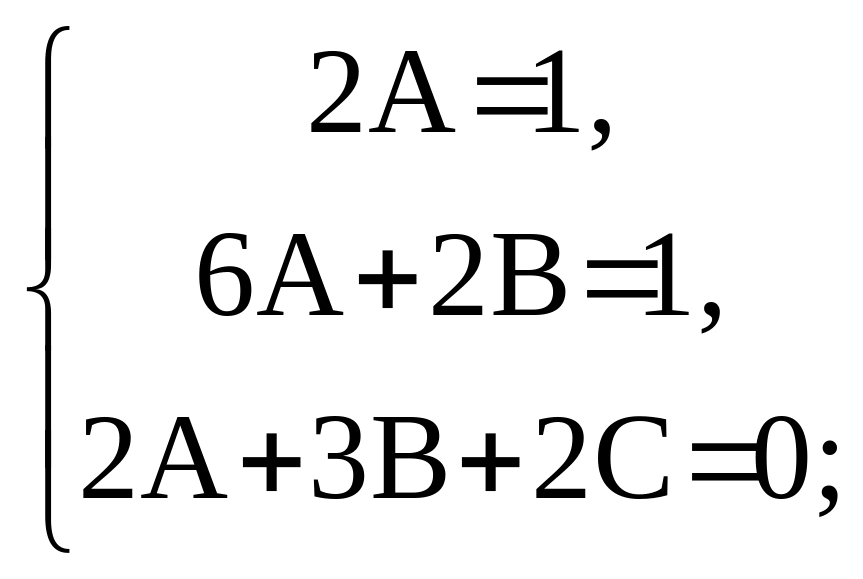
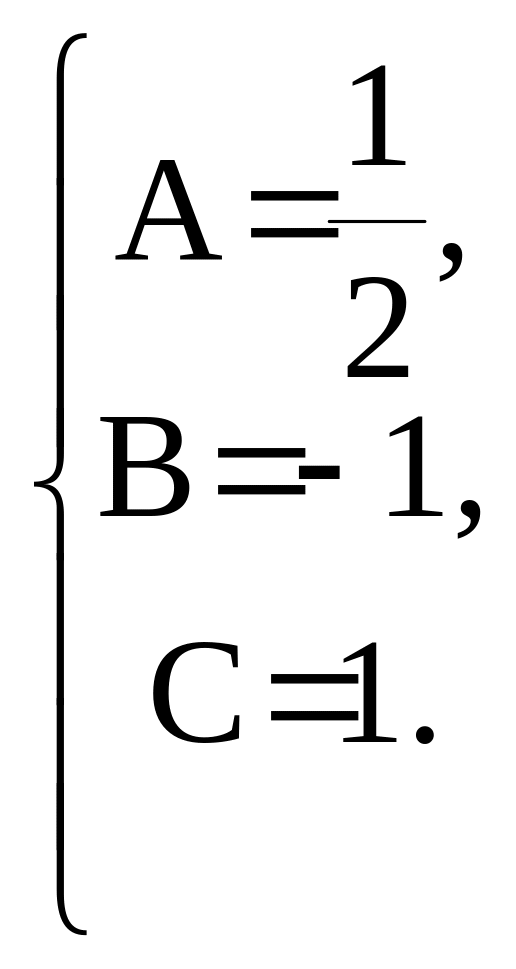
таким образом,
частное решение НЛДУ имеет вид:
![]() .
.
Общее решение НЛДУ
имеет вид:
![]()
Пример. Решить НЛДУ второго порядка: y+9y=6cos3x.
Найдем общее решение соответствующего ОЛДУ y+9y=0. Составим и решим характеристическое уравнение: к2+9=0, к1=3i, к2=-3i. Тогда уоо=С1cos3x+С2 sin3x.
Найдем частное решение данного НЛДУ. Функция f(x)=6cos3x является функцией специального вида f(x)=ex (Pn(x)cosx+Qm(x)sinx), при Pn(x)=6, Qm(x)=0 – многочлены нулевой степени от х, =0, =3, число (+i) является корнем характеристического уравнения кратности 1, поэтому частное решение будем искать в виде учн=e0xx1(Аcos3x+Вsin3x), или учн=x(Аcos3x+Вsin3x). Найдем значения неопределенных коэффициентов А, В.
учн=Аcos3x+Вsin3x+ x(-3Аsin3x+3Вcos3x);
учн=-3Аsin3x+3Вcos3x-3Аsin3x+3Вcos3x+x(-9Аcos3x-9Вsin3x)=
=(-6A-9Bx)sin3x+(-9Ax+6B)cos3x.
Подставим полученные значения в уравнение:
(-6A-9Bx)sin3x+(-9Ax+6B)cos3x+9x(Аcos3x+Вsin3x)=6cos3x;
(-6A-9Bx+9Bx)sin3x+(-9Ax+6B+9Ax)cos3x=6cos3x;
-6Asin3x+6Bcos3x=6cos3x;
![]()
![]() Таким образом,
частное решение НЛДУ имеет вид: учн=xsin3x.
Таким образом,
частное решение НЛДУ имеет вид: учн=xsin3x.
Общее решение НЛДУ имеет вид: уон=С1cos3x+С2 sin3x+ xsin3x.
Замечание 1. у каждого из рассмотренных методов есть свои преимущества и свои недостатки.
Метод вариации не зависит от вида правой части НЛДУ, однако этот метод достаточно трудоемкий
Преимуществом второго метода является простота, однако этот метод применим к ограниченному числу ДУ со специальной правой частью.
Замечание 2. Рассмотренные выше методы решения НЛДУ второго порядка с постоянными коэффициентами применяются и при решении НЛДУ высших порядков.
Пример. Решить НЛДУ четвертого порядка: yIV-3y=9x2.
Найдем общее
решение соответствующего ОЛДУ yIV-3y=0.
Составим и решим характеристическое
уравнение: к4-3к2=0,
к1=k2=0,
![]() .
.
Тогда
![]() ,
или
,
или
![]() .
.
Найдем частное решение данного НЛДУ. Функция f(x)=9x2 является функцией специального вида f(x)=exPn(x), при Pn(x)=9x2 – многочлен второй степени от х, =0 является корнем характеристического уравнения кратности 2, поэтому частное решение будем искать в виде учн=(Ах2+Вx+С)х2, или учн=Ах4+Вx3+Сх2. Найдем значения неопределенных коэффициентов А, В, С.
учн=4Ах3+3Вx2+2Сх;
учн=12Ах2+6Вx+2С;
учн=24Ах+6В;
yIVчн=24А.
Подставим полученные значения в уравнение:
24А-3(12Ах2+6Вx+2С)=9x2;
-36Ах2-18Вx+24А-6С=9x2;
так как многочлены, стоящие в левой и правой частях уравнения, равны при любых значениях переменной, то коэффициенты при соответствующих степенях х также должны быть равны; тогда
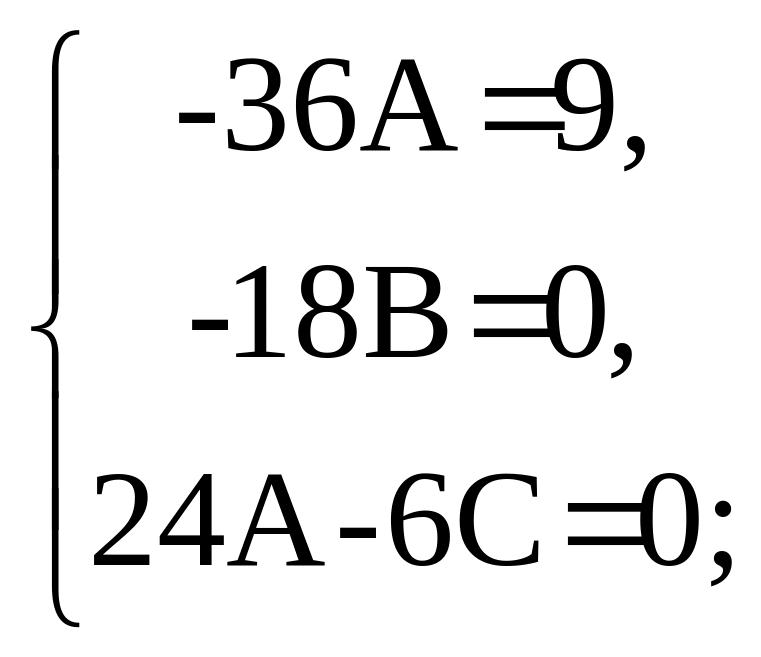
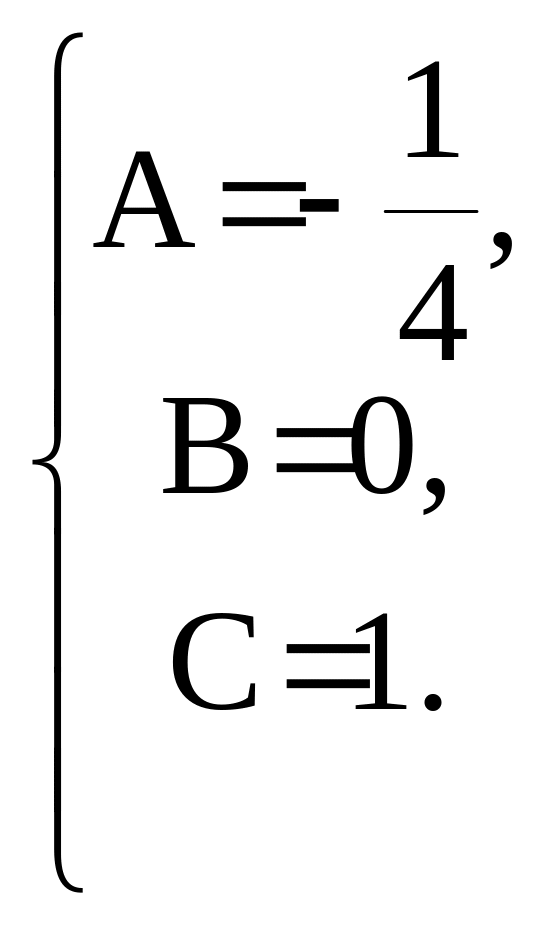
таким образом,
частное решение НЛДУ имеет вид:
учн=Ах4+Вx3+Сх2![]() .
.
Общее решение НЛДУ
имеет вид:
![]()
Пример.
Решить НЛДУ третьего порядка:
![]() .
.
Найдем общее
решение соответствующего ОЛДУ
![]() .
Составим и решим характеристическое
уравнение: к3-2к2-к+2=0,
к2(к-2)-(к-2)=0,
(к2-1)(к-2)=0,
к1=-1,
к2=1,
к3=2.
.
Составим и решим характеристическое
уравнение: к3-2к2-к+2=0,
к2(к-2)-(к-2)=0,
(к2-1)(к-2)=0,
к1=-1,
к2=1,
к3=2.
![]() .
.
Функция
![]() не является функцией специального вида.
Поэтому применим метод Лагранжа. Общее
решение НЛДУ будем искать в виде
не является функцией специального вида.
Поэтому применим метод Лагранжа. Общее
решение НЛДУ будем искать в виде
![]() .
.
Примем
![]() ,
,
![]() .
Тогда
.
Тогда
![]()
![]()
![]()
![]() .
.
Подставим полученные значения в ДУ:
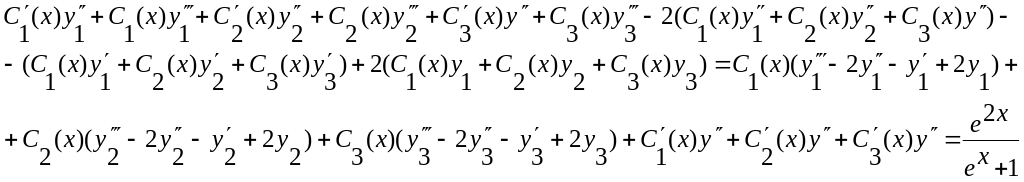
То есть
![]() .
Получим систему относительно неизвестных
С1(х),
С2(х),
С3(х):
.
Получим систему относительно неизвестных
С1(х),
С2(х),
С3(х):
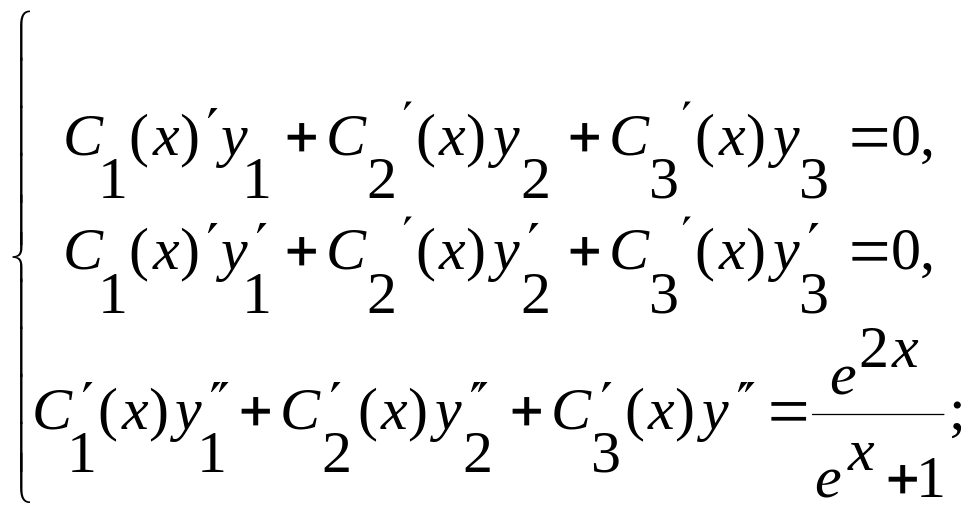
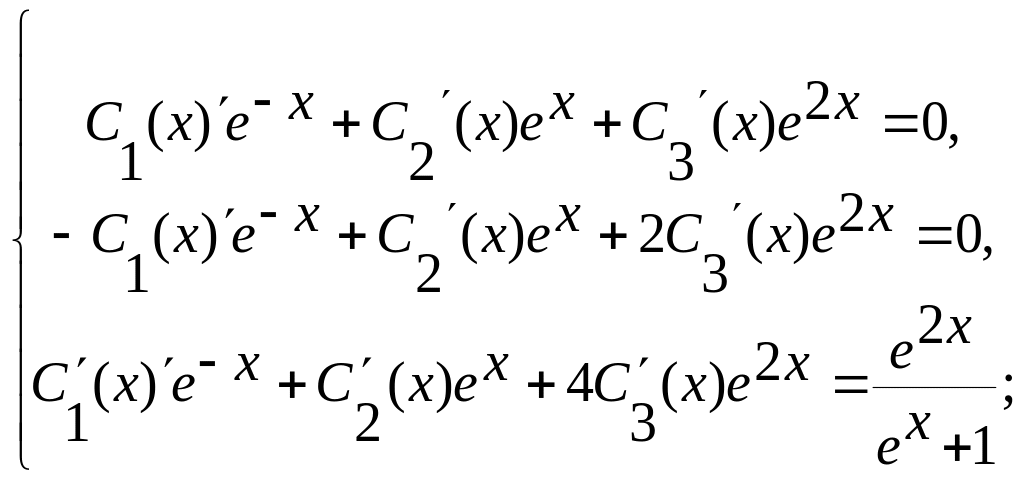 решив эту систему, найдем
решив эту систему, найдем
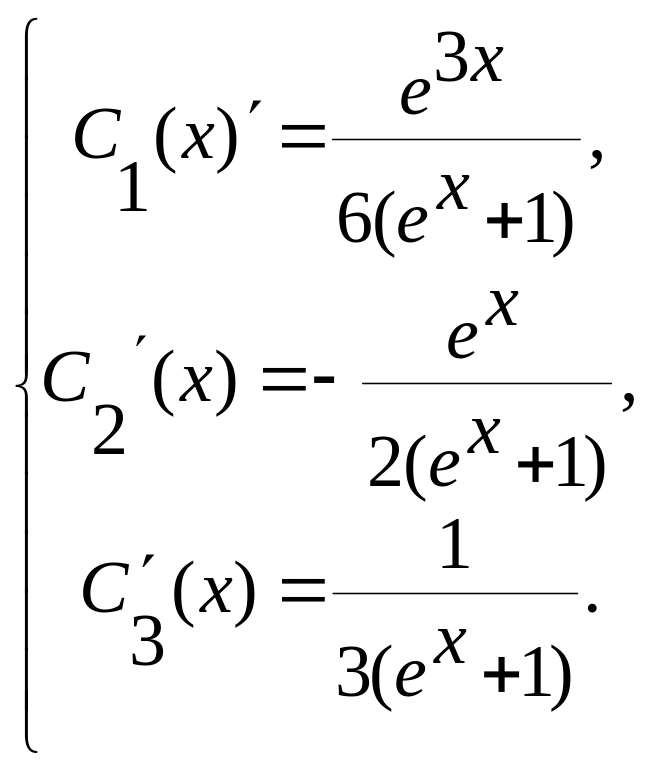 Проинтегрировав каждое из полученных
равенств, найдем значения функций С1(х),
С2(х), С3(х) и запишем общее
решение НЛДУ.
Проинтегрировав каждое из полученных
равенств, найдем значения функций С1(х),
С2(х), С3(х) и запишем общее
решение НЛДУ.
II. Примеры решения заданий практической части.
Найти частное решение дифференциального уравнения (решить задачу Коши).
а)
![]()
Решение.
1. Данное дифференциальное уравнение относится к уравнениям I типа, допускающих понижение порядка.
![]() разделим переменные:
разделим переменные:
![]() ;
;
![]() ;
проинтегрируем обе части:
;
проинтегрируем обе части:
![]() ;
;
![]() .
Повторим проделанные действия еще раз:
.
Повторим проделанные действия еще раз:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Воспользовавшись начальными условиями, определим значения С1 и С2.
![]() ;
;
![]() ;
С1=0;
;
С1=0;
![]() ;
;
![]() ;
С2=0.
;
С2=0.
Таким образом, частным решением является
функция
![]() .
.
Ответ: .
б)
![]() .
.
Решение.
1. Данное уравнение относится к III
типу дифференциальных уравнений,
допускающих понижение порядка. Понизим
порядок уравнения с помощью замены
![]() ,
тогда
,
тогда
![]() .
.
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
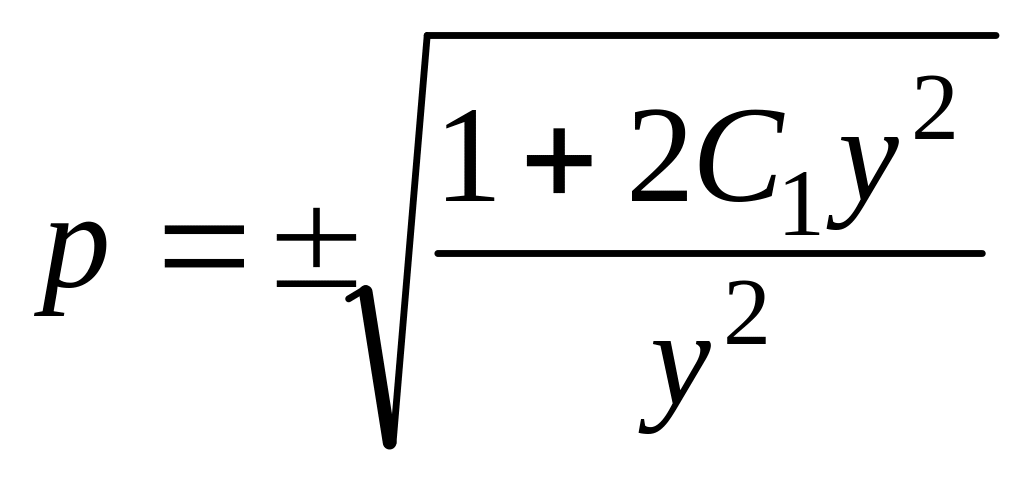 ,
,
![]() ;
;
Так как
,
то
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, общее решение данного дифференциального уравнения.
2. Воспользовавшись начальными условиями, определим значения С1 и С2.
Так как при х=1 у=0, у=1, получаем:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Следовательно, искомое частное решение
имеет вид:
![]() .
.
Ответ: .
2. Найти общее решение дифференциального уравнения, допускающего понижение порядка.
![]()
Решение.
Данное уравнение относится ко II
типу дифференциальных уравнений,
допускающих понижение порядка. Сделаем
подстановку
![]() ,
тогда
,
тогда
![]() .
Тогда
.
Тогда
![]() ;
разделим переменные:
;
разделим переменные:
![]() ,
,
![]() ;
проинтегрируем обе части равенства:
;
проинтегрируем обе части равенства:
![]() ,
,
![]() ,
выражая из последнего равенства я,
получаем:
,
выражая из последнего равенства я,
получаем:
![]() .
.
Так как
,
получаем
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Таким образом, общим решением уравнения является функция .
Ответ: .
Определить и записать структуру частного решения линейного неоднородного дифференциального уравнения по виду функции f(X).
![]() ,
если а)
,
если а)
![]() ,
б)
,
б)
![]() .
.
Решение.
Составим характеристическое уравнение и найдем его корни:
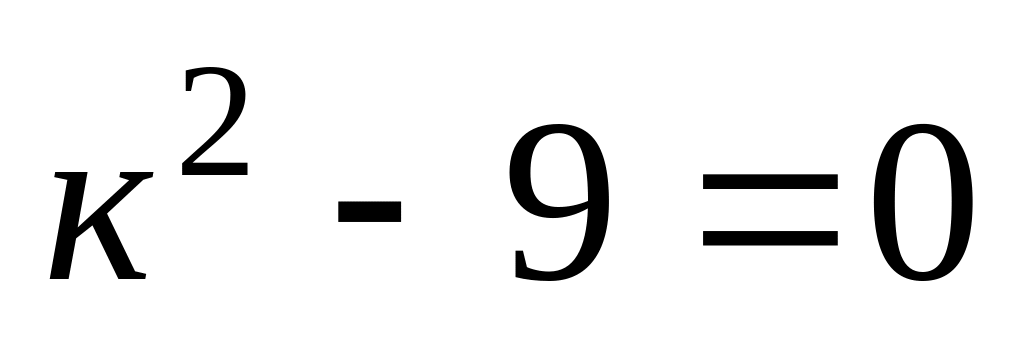 ,
к=3 или к=-3.
,
к=3 или к=-3.
а) данная функция соответствует первому специальному виду правой части f(x)=exPn(x), где =3, n=1 (степень многочлена 5-х).
=3 является корнем
кратности 1 характеристического
уравнения, поэтому частное решение
данного линейного неоднородного
дифференциального уравнения будет
иметь вид:
![]() или
или
![]() .
.
б)
или
![]() .
Данная функция соответствует второму
специальному виду правой части f(x)=ex
(Pn(x)cosx+Qm(x)sinx),
где =0,
=2,
n=0,
m=1.
.
Данная функция соответствует второму
специальному виду правой части f(x)=ex
(Pn(x)cosx+Qm(x)sinx),
где =0,
=2,
n=0,
m=1.
Так как +i=0+2i
не является корнем характеристического
уравнения, то частное решение будем
искать в виде
![]() или
или
![]() .
.
Ответ: а) ; б) .
4. Найти общее решение линейного неоднородного дифференциального уравнения.
![]()
Решение.
1. Составим характеристическое уравнение
и найдем его корни:
![]() ,
к=-1 или к=4.
,
к=-1 или к=4.
Тогда
![]() .
.
2. Правая часть
исходного уравнения имеет вид
![]() ,
что соответствует первому специальному
виду правой части f(x)=exPn(x),
где =-1,
n=1
(степень многочлена 6х).
,
что соответствует первому специальному
виду правой части f(x)=exPn(x),
где =-1,
n=1
(степень многочлена 6х).
=-1 является корнем
кратности 1 характеристического
уравнения, поэтому частное решение
данного линейного неоднородного
дифференциального уравнения будет
иметь вид:
![]() или
или
![]() .
.
Найдем неопределенные коэффициенты А и В.
![]() ,
,
![]() или
или
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Подставим найденные
выражения для у, у,
у
в исходное уравнение:
![]() ,
разделим обе части уравнения на е-х:
,
разделим обе части уравнения на е-х:
![]() ;
перегруппируем левую часть уравнения
по степеням х:
;
перегруппируем левую часть уравнения
по степеням х:
![]() ,
,
![]() ,
,
составим систему уравнений, приравняв
коэффициенты при одинаковых степенях
х в левой и правой части:
![]()
![]()
Таким образом, частное решение линейного
неоднородного дифференциального
уравнения имеет вид:
![]() .
.
3. Общее решение
данного линейного неоднородного
дифференциального уравнения будет
иметь вид:
![]() или
или
![]() .
.
Ответ: .
5. Найти частное решение линейного неоднородного дифференциального уравнения, удовлетворяющее данным начальным условиям (решить задачу Коши).
![]()
Решение.
1. Составим характеристическое уравнение
и найдем его корни:
![]() ,
,
![]() или
или
![]() .
.
Тогда
![]() .
.
2. Правая часть
исходного уравнения имеет вид
![]() или
или
![]() ,
что соответствует второму специальному
виду правой части f(x)=ex
(Pn(x)cosx+Qm(x)sinx),
где =0,
=1,
n=0,
m=0.
,
что соответствует второму специальному
виду правой части f(x)=ex
(Pn(x)cosx+Qm(x)sinx),
где =0,
=1,
n=0,
m=0.
Так как +i=0+i
не является корнем характеристического
уравнения, то частное решение будем
искать в виде
![]() или
или
![]() .
.
Найдем неопределенные коэффициенты А и В.
![]() ,
,
![]() ,
,
![]()
Подставим найденные выражения для у, у, у в исходное уравнение:
![]() ,
,
![]() ,
,
![]() ;
;
составим систему уравнений, приравняв
соответствующие коэффициенты в левой
и правой части:
![]()
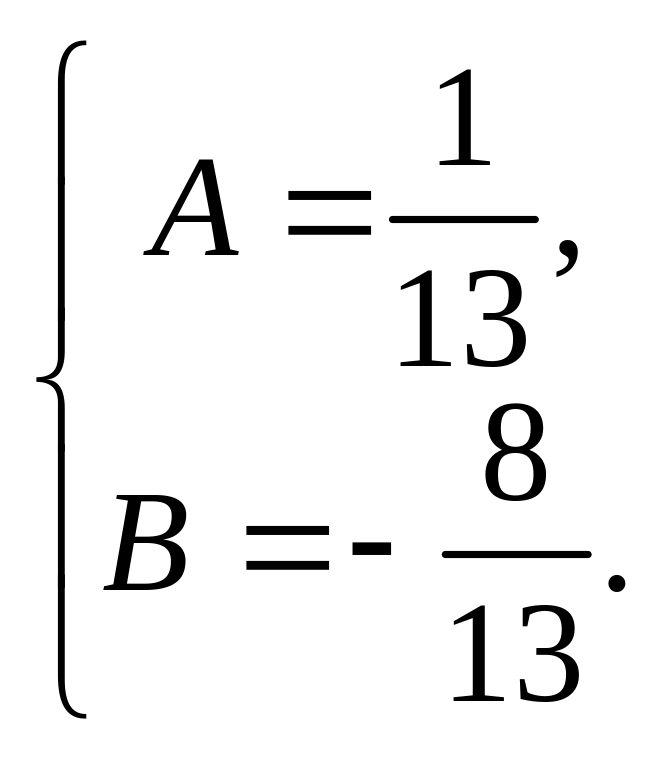
Таким образом, частное решение линейного
неоднородного дифференциального
уравнения имеет вид:
![]() .
.
3. Общее решение
данного линейного неоднородного
дифференциального уравнения будет
иметь вид:
![]() .
.
4. Воспользовавшись начальными условиями, определим значения С1 и С2.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким образом,
частным решением исходного линейного
неоднородного дифференциального
уравнения, удовлетворяющим заданным
начальным условием, является функция
![]() .
.
Ответ: .
6. Решить дифференциальное уравнение методом вариации произвольной постоянной (методом Лагранжа).
![]() .
.
Решение.
1. Найдем общее решение соответствующего
линейного однородного дифференциального
уравнения
![]() .
.
![]() ,
к=1 или к=-1. Тогда общее решение имеет
вид:
,
к=1 или к=-1. Тогда общее решение имеет
вид:
![]() .
.
2. Найдем общее решение линейного неоднородного дифференциального уравнения, считая С1=С1(х) и С2=С2(х) некоторыми пока неизвестными функциями.
С1(х) и С2(х) определим из системы уравнений:
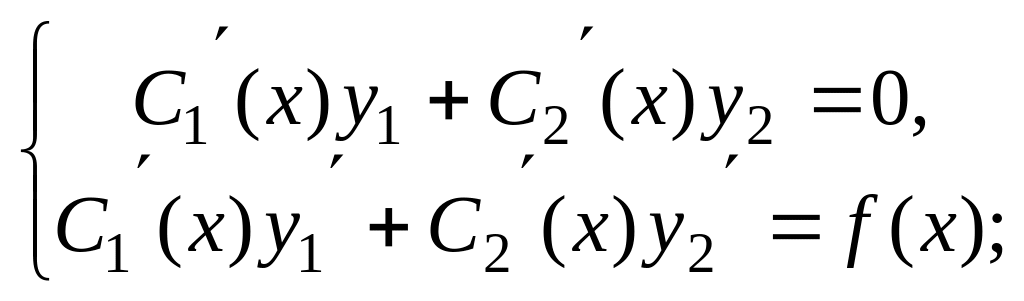
Для данного уравнения эта система имеет
вид:

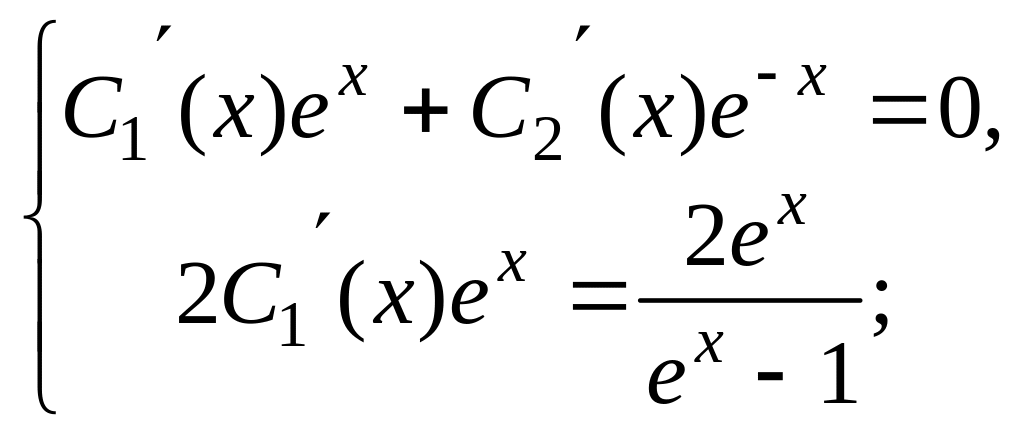
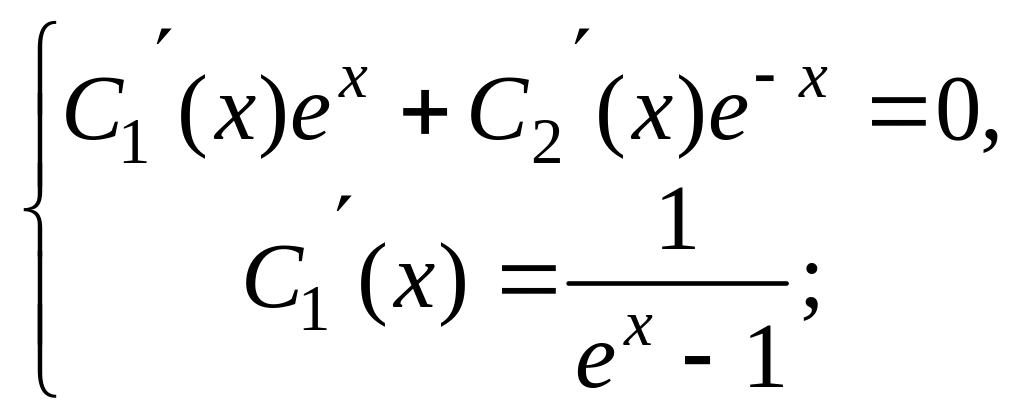
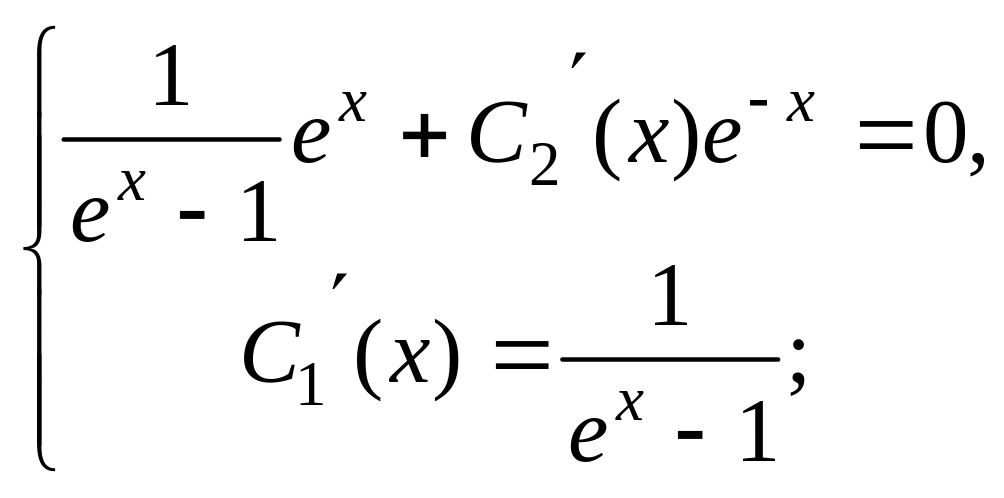
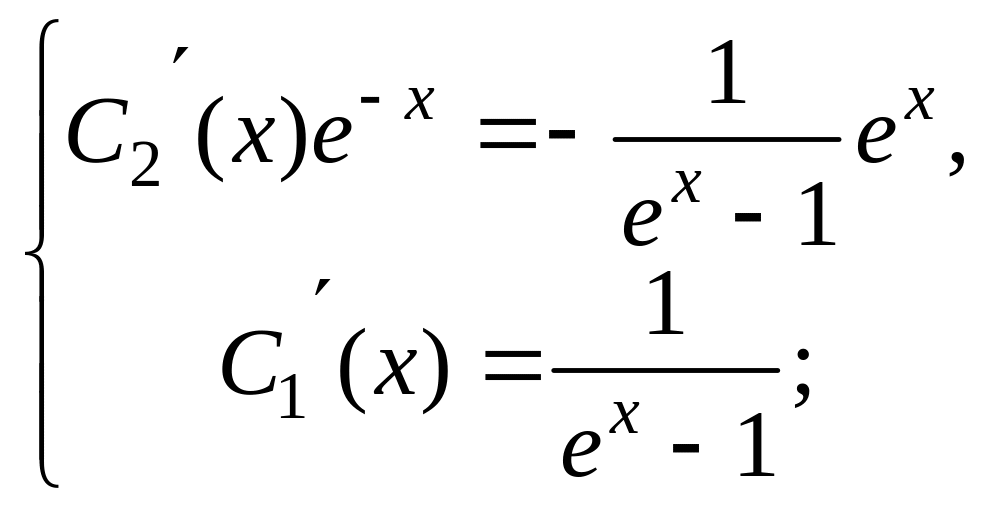
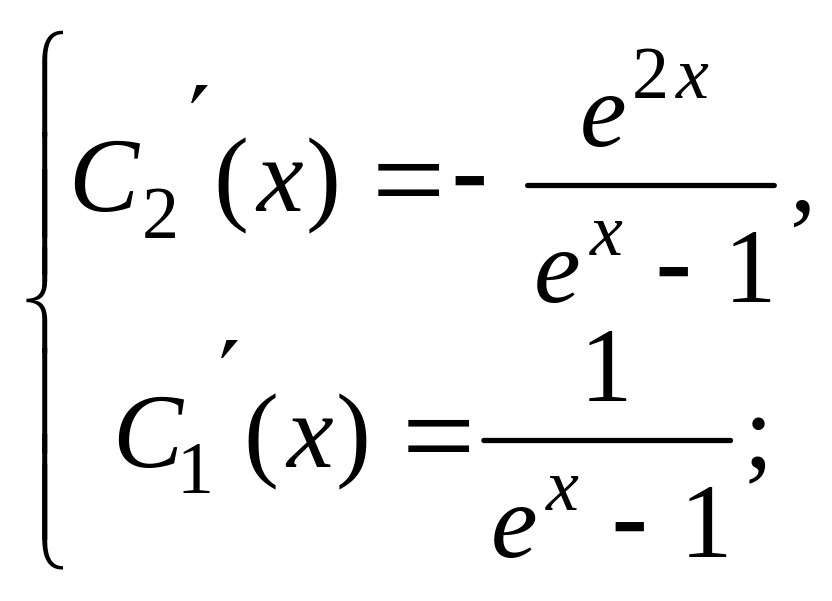
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Следовательно, общее решение исходного
линейного неоднородного дифференциального
уравнения будет иметь вид:
![]() .
.
Ответ: .
III. Задания для практической части.
1. Найти частное решение дифференциального уравнения (решить задачу Коши).
1.1. а) у=sinx, y(0)=1, y(0)=0, y(0)=0; б)
 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
1.2. а)
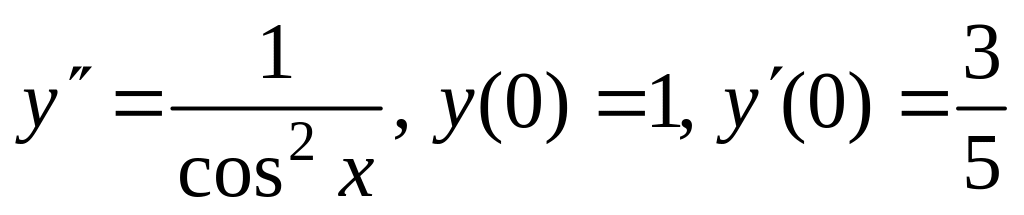 ;
б)
;
б)
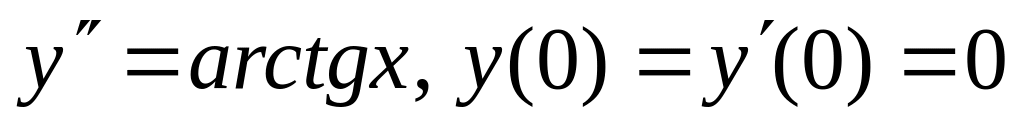 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
1.3. а)
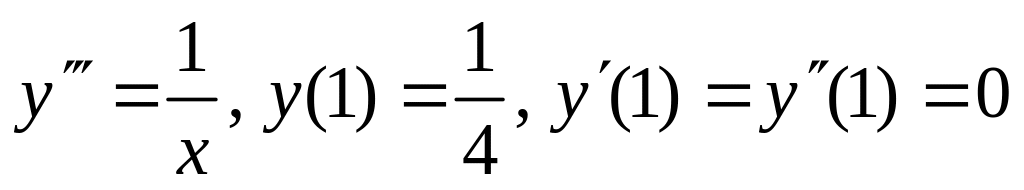 ;
б)
;
б)
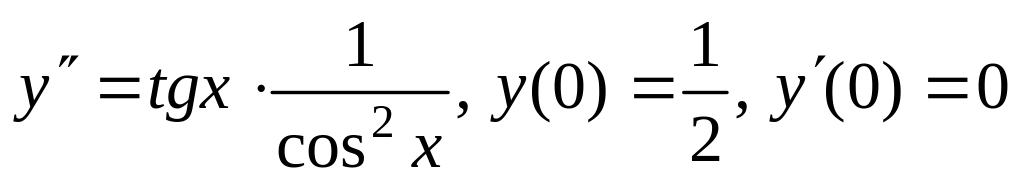 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
1.4. а)
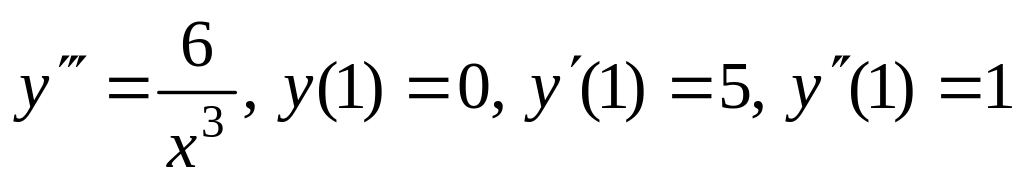 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
1.5. а)
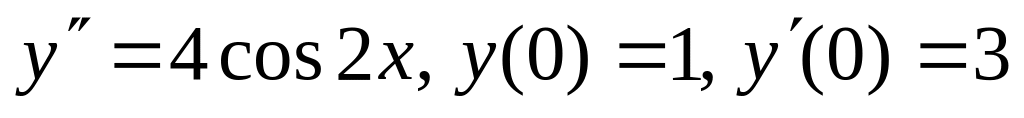 ;
б)
;
б)
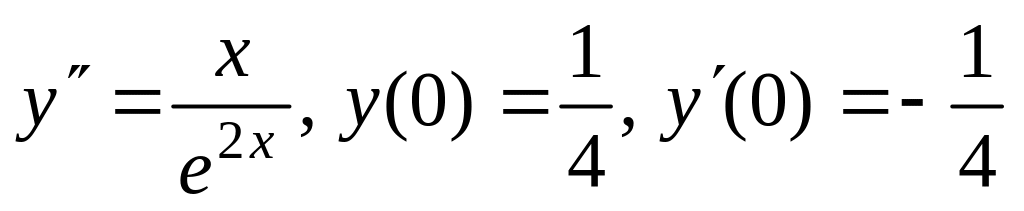 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
1.6. а)
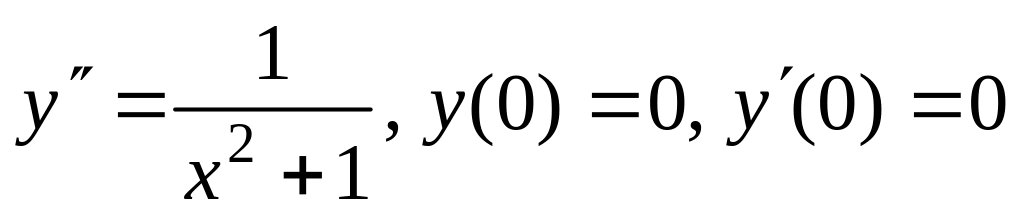 ;
б)
;
б)
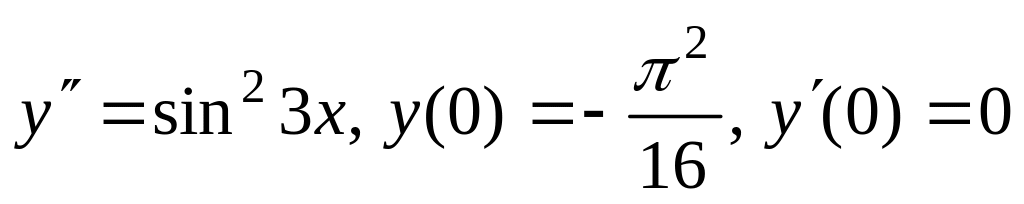 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
1.7. а)
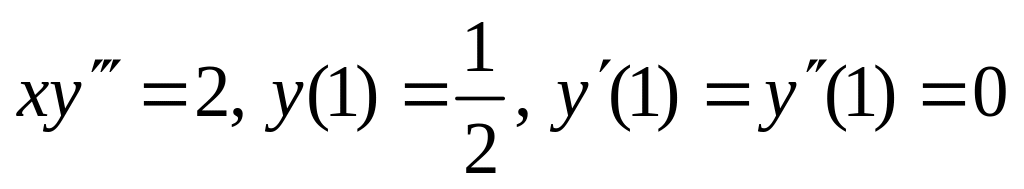 ;
б)
;
б)
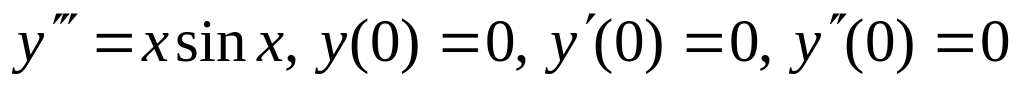 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
1.8. а)
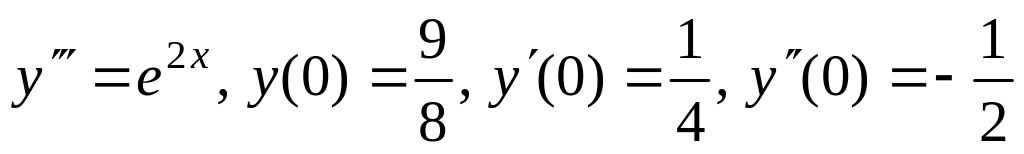 ;
б)
;
б)
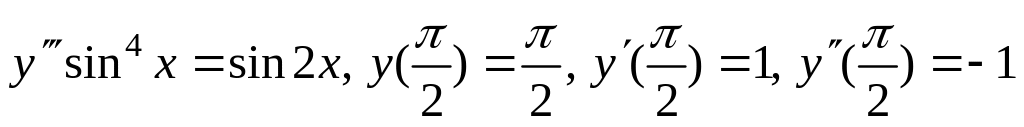 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
1.9. а)
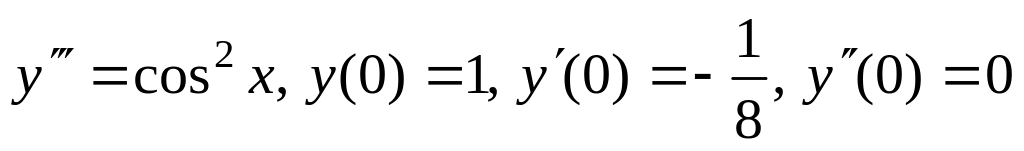 ;
б)
;
б)
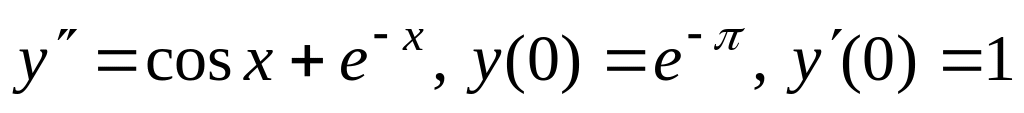 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
1.10. а)
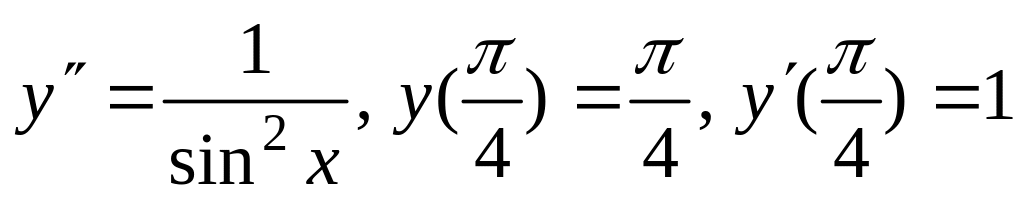 ;
б)
;
б)
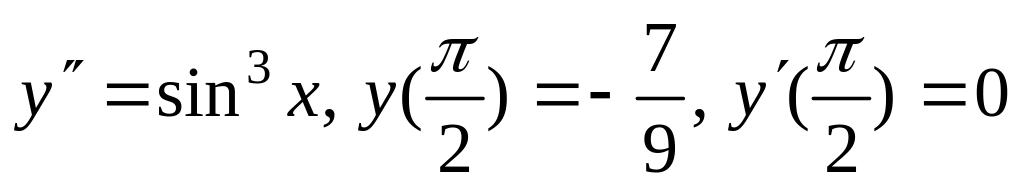 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
2. Найти общее решение дифференциального уравнения, допускающего понижение порядка.
2.1. а)
![]() ;
б)
;
б)
![]() ;
2.2. а)
;
2.2. а)
![]() ;
б)
;
б)
![]() ;
;
2.3. а)
![]() ;
б)
;
б)
![]() ; 2.4.
а)
; 2.4.
а)
![]() ;
б)
;
б)
![]() ;
;
2.5. а)
![]() ;
б)
;
б)
![]() ; 2.6.
а)
; 2.6.
а)
![]() ;
б)
;
б)
![]() ;
;
2.7. а)
![]() ;
б)
;
б)
![]() ; 2.8.
а)
; 2.8.
а)
![]() ;
б)
;
б)
![]() ;
;
2.9. а)
![]() ;
б)
;
б)
![]() ; 2.10.
а)
; 2.10.
а)
![]() ;
б)
;
б)
![]() .
.
3. Найти общее решение линейного однородного дифференциального уравнения.
3.1. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
3.2. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
3.3. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
3.4. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
3.5. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
3.6. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
3.7. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
3.8. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
3.9. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
3.10. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() .
.
4. Определить и записать структуру частного решения линейного неоднородного дифференциального уравнения по виду функции f(x).
4.1.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() ;
;
4.2.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() ;
;
4.3.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() ;
;
4.4.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() ;
;
4.5.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() ;
;
4.6.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() ;
;
4.7.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() ;
;
4.8.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() ;
;
4.9.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() ;
;
4.10.
![]() ,
а)
,
а)
![]() ;
б)
;
б)
![]() .
.
5. Найти общее решение линейного неоднородного дифференциального уравнения.
5.1. а)
![]() ;
б)
;
б)
![]() ;
;
5.2. а)
![]() ;
б)
;
б)
![]() ;
;
5.3. а)
![]() ;
б)
;
б)
![]() ;
;
5.4. а)
![]() ;
б)
;
б)
![]() ;
;
5.5. а)
![]() ;
б)
;
б)
![]() ;
;
5.6. а)
![]() ;
б)
;
б)
![]() ;
;
5.7. а)
![]() ;
б)
;
б)
![]() ;
;
5.8. а)
![]() ;
б)
;
б)
![]() ;
;
5.9. а)
![]() ;
б)
;
б)
![]() ;
;
5.10. а)
![]() ;
б)
;
б)
![]() .
.
6. Найти частное решение линейного неоднородного дифференциального уравнения, удовлетворяющее данным начальным условиям (решить задачу Коши).
6.1. а)
![]() ;
;
б)
![]() ;
;
6.2. а)
![]() ;
;
б)
![]() ;
;
6.3. а)
![]() ;
;
б)
![]() ;
;
6.4. а)
![]() ;
;
б)
![]() ;
;
6.5. а)
![]() ;
;
б)
![]() ;
;
6.6. а)
![]() ;
;
б)
![]() ;
;
6.7. а)
![]() ;
;
б)
![]() ;
;
6.8. а)
![]() ;
;
б)
![]() ;
;
6.9. а)
![]() ;
;
б)
![]() ;
;
6.10. а)
![]() ;
;
б)
![]() .
.
7. Решить дифференциальное уравнение методом вариации произвольной постоянной (методом Лагранжа).
7.1. а)
![]() ;
б)
;
б)
![]() ;
;
7.2. а)
![]() ;
б)
;
б)
![]() ;
;
7.3. а)
![]() ;
б)
;
б)
![]() ;
;
7.4. а)
![]() ;
б)
;
б)
![]() ;
;
7.5. а)
![]() ;
б)
;
б)
![]() ;
;
7.6. а)
![]() ;
б)
;
б)
![]() ;
;
7.7. а)
![]() ;
б)
;
б)
![]() ;
;
7.8. а)
![]() ;
б)
;
б)
![]() ;
;
7.9. а)
![]() ;
б)
;
б)
![]() ;
;
7.10. а)
![]() ;
б)
;
б)
![]() .
.
