1.3.2. Структура общего решения линейного дифференциального уравнения.

Будем говорить, что ОЛДУ y⁽ⁿ⁾+a_n-1(x)y^(n-1)+ a_n-2(x)y^(n-2)+…+a₁(x)y+a₀(x)y=0 соответствует НЛДУ y⁽ⁿ⁾+a_n-1(x)y^(n-1)+ a_n-2(x)y^(n-2)+…+a₁(x)y+a₀(x)y=f(x), если левые части этих уравнений совпадают.

Теорема. (структура общего решения НЛДУ)

Пусть функции у₁(х), у₂(х),…, у_n(х) составляют фундаментальную систему решений ОЛДУ y⁽ⁿ⁾+a_n-1(x)y^(n-1)+ a_n-2(x)y^(n-2)+…+a₁(x)y+a₀(x)y=0, соответствующего НЛДУ

y⁽ⁿ⁾+a_n-1(x)y^(n-1)+ a_n-2(x)y^(n-2)+…+a₁(x)y+a₀(x)y=f(x); – некоторое произвольное решение уравнения y⁽ⁿ⁾+a_n-1(x)y^(n-1)+ a_n-2(x)y^(n-2)+…+a₁(x)y+a₀(x)y=f(x). тогда функция

у(х)= + С₁у₁(х)+С₂у₂(х)+…+С_nу_n(х) будет являться общим решением НЛДУ (1).

Замечание. Будем обозначать (общее решение ОЛДУ); (частное решение НЛДУ). Тогда общее решение НЛДУ

y⁽ⁿ⁾+a_n-1(x)y^(n-1)+ a_n-2(x)y^(n-2)+…+a₁(x)y+a₀(x)y=f(x) будет иметь вид: у_он=у_оо+у_чн.

1.3.3. Общее решение однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.

Характеристическое уравнение.

ОЛДУ второго порядка имеет вид: y+ay+by=0. (1)

Решение уравнения (1) будем искать в виде у(х)= е^кх; тогда у(х)=ке^кх, у(х)=к²е^кх. Подставим в уравнение (1):

к²е^кх+аке^кх+bе^кх=0. разделим обе части уравнения на е^кх (е^кх0):

к²+ак+b=0. (2)

Очевидно, для того чтобы функция у(х)=е^кх была решением уравнения (1), необходимо и достаточно чтобы к являлось решением уравнения (2), которое называют характеристическим уравнением ОЛДУ (1).

В процессе решения уравнения (2) возможен один из трех вариантов:

• корни уравнения являются различными действительными числами;

• корни уравнения являются равными действительными числами;

• корни уравнения являются различными комплексными числами.

1. Случай различных действительных корней.

Пусть к₁ и к₂ различные действительные корни характеристического уравнения к²+ак+b=0.

Рассмотрим функции и . Очевидно, каждая из них является решением ОЛДУ (1). Докажем, что у₁(х) и у₂(х) образуют ФСР. Составим для них определитель Вронского:

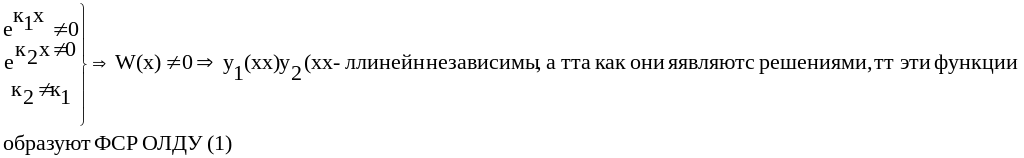
Пример. у-2у-3у=0.

Составим и решим характеристическое уравнение: к²-2к-3=0. к₁=3, к₂=-1. Тогда общее решение данного ОЛДУ имеет вид: .

2. Случай кратных корней.

Пусть характеристическое уравнение к²+ак+b=0 имеет два равных корня: к₁=к₂=к, . Тогда функция является решением ОЛДУ (1). Покажем, что функция так же является решением этого ОЛДУ.

, , .

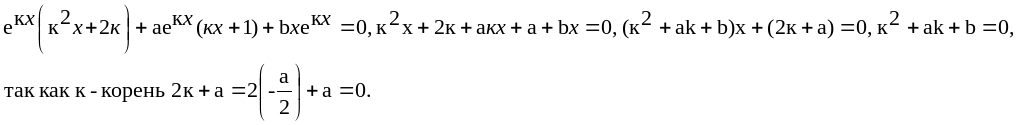
Следовательно, является решением ОЛДУ.

Покажем, что функции и образуют ФСР.

. Следовательно, функции и образуют ФСР, а следовательно, общее решение ОЛДУ в этом случае имеет вид: .

3. Случай комплексно-сопряженных корней.

Если определитель D<0, то квадратное уравнение имеет комплексные корни к₁ и к₂, причем

к₁=+i, к₂=-i. Тогда ОЛДУ будет иметь два решения:

и . Имеет место формула Эйлера: .

Тогда , .

Рассмотрим функции и .

. Полученные функции являются решениями ОЛДУ по свойству 2. Проверим, образуют ли данные функции ФСР.

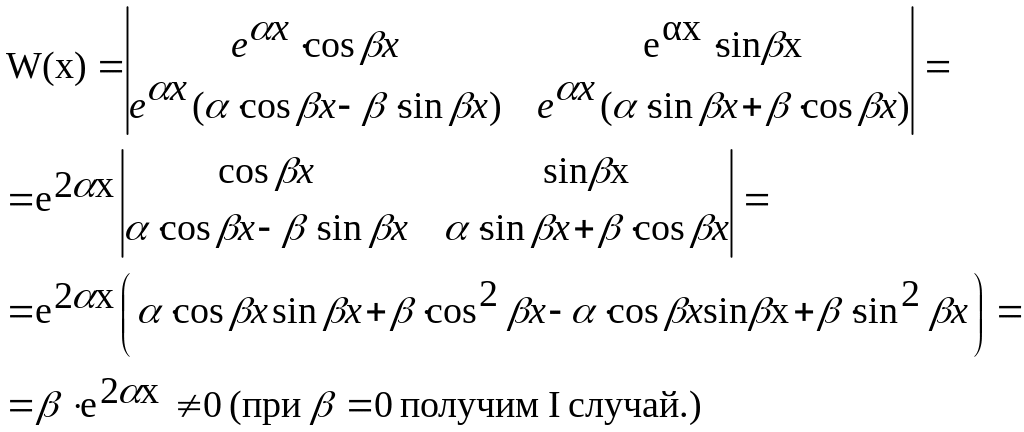
Таким образом, функции образуют ФСР. Тогда общее решение ОЛДУ в случае различных комплексных корней характеристического уравнения имеет вид: .

Пример. Решить ОЛДУ второго порядка 1) у-2у+у=0; 2) у+у+у=0.

1) Составим и решим характеристическое уравнение: к²-2к+1=0. к₁=к₂=1. Тогда общее решение данного ОЛДУ имеет вид: .

2) Составим и решим характеристическое уравнение: к²+к+1=0. D=-3<0,

. Тогда общее решение ОЛДУ имеет вид: