
Державний вищий навчальний заклад
«Запорізький національний університет»
Міністерства освіти і науки України
О.І. Александров, Н.І.–В. Манько
ЗБІРНИК ІНДИВІДУАЛЬНИХ ЗАВДАНЬ
З ФУНКЦІОНАЛЬНОГО АНАЛІЗУ
для студентів математичного факультету
Затверджено
вченою радою ЗНУ
Протокол № від
Запоріжжя
2011
УДК
ББК
Александров О.І., Манько Н.І.–В. Збірник індивідуальних завдань з функціонального аналізу для студентів математичного факультету.–Запоріжжя: ЗНУ, 2011.– 66 с.
Збірник індивідуальних завдань призначений для студентів III–V курсів та магістрів математичного факультету спеціальності «математика» за всіма освітньо-кваліфікаційними рівнями підготовки (бакалавр, спеціаліст, магістр). У ньому подано варіанти індивідуальних завдань, передбачених робочими програмами з дисциплін «Функціональний аналіз», «Теорія міри та інтегралу», «Вибрані питання функціонального аналізу», «Вибрані питання нелінійного функціонального аналізу і теорії операторів», а також наведено список рекомендованої літератури із зазначених предметів.
Рецензент Приварников А.К.
Відповідальний за випуск Манько Н.І.–В.
ЗМІСТ
Вступ……………………………………………………………………………… 1 Аналіз у метричних просторах……………………………………………….. 2 Лінійний функціональний аналіз……………………………………………... 3 Вибрані питання нелінійного функціонального аналізу і теорії операторів 4 Вибрані питання функціонального аналізу………………………………….. 5 Теорія міри та інтегралу………………………………………………………. |
4 5 19 30 37 48 |
ВСТУП
Цей збірник завдань розроблено для студентів університетів, які отримують вищу освіту за спеціальністю «Математика». Він містить у собі 115 варіантів індивідуальних завдань з дисциплін «Функціональний аналіз», «Теорія міри та інтегралу», «Вибрані питання функціонального аналізу», «Вибрані питання нелінійного функціонального аналізу і теорії операторів». Перелічені дисципліни поєднує те, що всі вони є повязаними одна з одною частинами функціонального аналізу – однієї з найважливіших областей сучасної математики.
Задачі, обєднані в одному варіанті, мають характер семестрового завдання з відповідної дисципліни. Вони отримуються індивідуально кожним студентом, який повинен виконати і захистити це завдання протягом семестру. Робота над виконанням завданням має бути самостійною і повинна спиратися на методики, які викладені на лекціях, практичних заняттях, або містяться в рекомендованій літературі. Оцінка, яку отримує студент за виконане завдання, повина враховувати не зовсім однаковий рівень складностізадач цього завдання і впливати на атестаційні показники модульного контроля, а також мати свій внесок у загальну підсумкову оцінку з відповідної дисципліни.
Збірник складається з п’яти розділів, перші два з яких відповідають семестровим складовим частинам дисципліни «Функціональний аналіз», а останні три розділи містять у собі завдання з дисциплін, назви яких співпадають з назвами цих розділів.
1 Аналіз у метричних просторах
ВАРІАНТ 1
Нехай
 і
і
 – довільні множини,
– довільні множини,
 і
і
 – довільні підмножини множини
;
– довільні підмножини множини
;
 – довільне взаємно однозначне
відображення. Чи виконується співвідношення
– довільне взаємно однозначне
відображення. Чи виконується співвідношення
 ?
?Множини , і відображення
 визначені співвідношеннями:
визначені співвідношеннями:
 .
Чи існує відображення
.
Чи існує відображення
 ,
яке є оберненим до
?
,
яке є оберненим до
?Чи збігається у просторі
 послідовність
послідовність
 його елементів, для якої
його елементів, для якої
 ,
,

Чи збігається у просторі
 послідовність
послідовність
 його елементів, якщо
його елементів, якщо
 ?
?Чи є множина строго зростаючих на відрізку
 функцій простору
функцій простору
 відкритою у цьому просторі?
відкритою у цьому просторі?Чи є множина
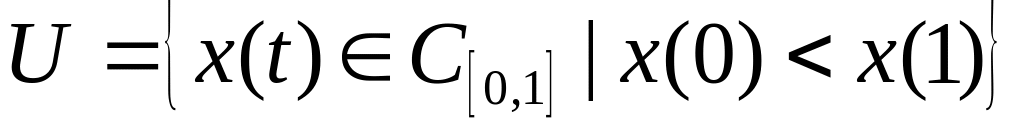 замкненою у просторі
?
замкненою у просторі
?На множині
 визначена метрика
визначена метрика
 .Чи
є отриманий таким чином метричний
простір повним?
.Чи
є отриманий таким чином метричний
простір повним?
ВАРІАНТ 2
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне взаємно однозначне відображення. Чи виконується співвідношення
 ?
?Множини , і відображення визначені співвідношеннями:
 .
Чи існує відображення
.
Чи існує відображення
 ,
яке є оберненим до
,
яке є оберненим до
 ?
?Чи збігається у просторі послідовність
 його елементів, для якої
його елементів, для якої
 ,
,

Чи збігається у просторі
 послідовність
послідовність
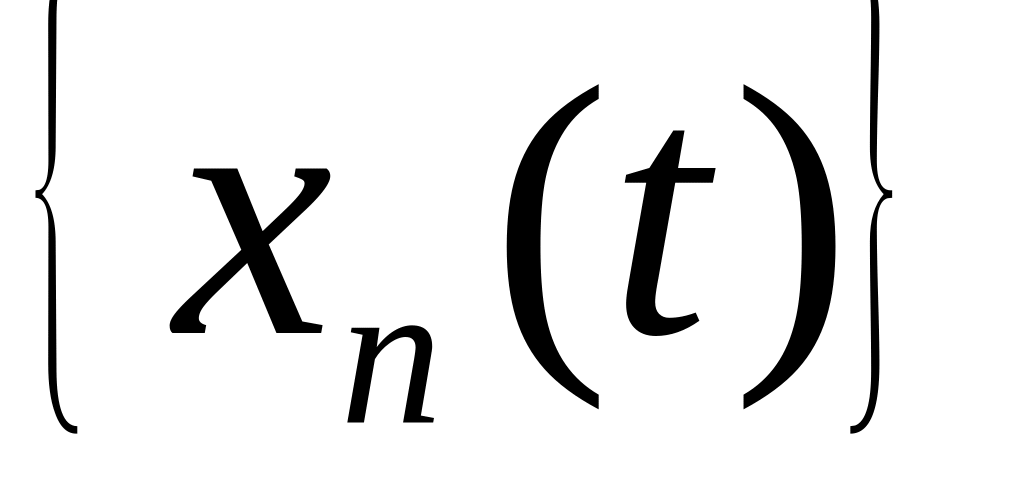 його елементів, якщо
його елементів, якщо
 ?
?Чи є множина неспадних на відрізку
 функцій простору
відкритою у цьому просторі?
функцій простору
відкритою у цьому просторі?Чи є множина
 замкненою у просторі
?
замкненою у просторі
?На множині
 визначена метрика
визначена метрика
 .Чи
є отриманий таким чином метричний
простір повним?
.Чи
є отриманий таким чином метричний
простір повним?
ВАРІАНТ 3
Нехай і – довільні множини,
 – довільна підмножина множини
;
– довільне взаємно однозначне
відображення. Чи виконується співвідношення
– довільна підмножина множини
;
– довільне взаємно однозначне
відображення. Чи виконується співвідношення
 ?
?Множини , і відображення
 визначені співвідношеннями:
визначені співвідношеннями:
 .
Чи існує відображення
.
Чи існує відображення
 ,
яке є оберненим до
?
,
яке є оберненим до
?Чи збігається у просторі послідовність його елементів, для якої
 ,
,

Чи збігається у просторі
 послідовність
послідовність
 його елементів, якщо
його елементів, якщо
 ?
?Чи є множина строго зростаючих на відрізку
 функцій простору
функцій простору
 відкритою у цьому просторі?
відкритою у цьому просторі?Чи є множина
 замкненою у просторі
замкненою у просторі
 ?
?На множині
 визначена метрика
визначена метрика
 .Чи
є отриманий таким чином метричний
простір повним?
.Чи
є отриманий таким чином метричний
простір повним?
ВАРІАНТ 4
Нехай і – довільні множини,
 – довільна підмножина множини
;
– довільне взаємно однозначне
відображення. Чи виконується співвідношення
– довільна підмножина множини
;
– довільне взаємно однозначне
відображення. Чи виконується співвідношення
 ?
?Множини , і відображення визначені співвідношеннями:
 .
Чи існує відображення
.
Чи існує відображення
 ,
яке є оберненим до
?
,
яке є оберненим до
?Чи збігається у просторі послідовність його елементів, для якої
 ,
,

Чи збігається у просторі послідовність його елементів, для якої

Чи є множина всіх неспадних на відрізку функцій простору
 відкритою у цьому просторі?
відкритою у цьому просторі?Чи є множина
 замкненою у просторі
?
замкненою у просторі
?На множині
 всіх ірраціональних чисел визначена
метрика
всіх ірраціональних чисел визначена
метрика
 .Чи
є отриманий таким чином метричний
простір повним?
.Чи
є отриманий таким чином метричний
простір повним?
ВАРІАНТ 5
Нехай і – довільні множини,
 і
і
 – довільні підмножини множини
;
– довільне відображення. Чи виконується
співвідношення
– довільні підмножини множини
;
– довільне відображення. Чи виконується
співвідношення
 ?
?Множини , і відображення визначені співвідношеннями:
 .
Чи існує відображення
,
яке є оберненим до
?
.
Чи існує відображення
,
яке є оберненим до
?Чи збігається у просторі послідовність його елементів, для якої ,

Чи збігається у просторі
 послідовність
його елементів, якщо
послідовність
його елементів, якщо
 ?
?Чи є множина
 відкритою
у просторі
?
відкритою
у просторі
?Чи є множина
 замкненою у просторі
?
замкненою у просторі
?На множині визначених на відрізку функцій
 задана метрика
задана метрика
 .
Чи є отриманий таким чином метричний
простір повним?
.
Чи є отриманий таким чином метричний
простір повним?
ВАРІАНТ 6
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне відображення. Чи виконується співвідношення
 ?
?Множини , і відображення визначені співвідношеннями:

 ,
,
 .
Чи існує відображення
,
яке є оберненим до
?
.
Чи існує відображення
,
яке є оберненим до
?Чи збігається у просторі послідовність його елементів, для якої
 ?
?Чи збігається у просторі послідовність його елементів, якщо
 ?
?Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина
 замкненою у просторі
замкненою у просторі
 ?
?На множині
 всіх упорядкованих сукупностей
всіх упорядкованих сукупностей
 дійсних чисел визначена метрика
дійсних чисел визначена метрика
 ,
де
,
де
 ,
,
 .
Довести, що отриманий таким чином
метричний простір є повним?
.
Довести, що отриманий таким чином
метричний простір є повним?
ВАРІАНТ 7
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне відображення. Чи виконується співвідношення
 ?
?Множини , і відображення визначені співвідношеннями:
 .
Чи існує відображення
,
яке є оберненим до
?
.
Чи існує відображення
,
яке є оберненим до
?Чи збігається у просторі
 послідовність
його елементів, для якої
послідовність
його елементів, для якої
 ?
?Чи збігається у просторі послідовність його елементів, для якої

Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина
 замкненою у просторі
замкненою у просторі
 ?
?На множині всіх упорядкованих сукупностей дійсних чисел визначена метрика
 ,
де
,
де
 ,
,
 .Чи
є отриманий таким чином метричний
простір повним?
.Чи
є отриманий таким чином метричний
простір повним?
ВАРІАНТ 8
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне взаємно однозначне відображення. Чи виконується співвідношення
 ?
?Множини , і відображення визначені співвідношеннями:
 .
Чи існує відображення
,
яке є оберненим до
?
.
Чи існує відображення
,
яке є оберненим до
?Чи збігається у просторі послідовність його елементів, для якої
 ?
?Чи збігається у просторі послідовність його елементів, якщо
 ?
?Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина
 замкненою у просторі
?
замкненою у просторі
?Довести, що метричний простір
 є повним.
є повним.
ВАРІАНТ 9
Нехай і – довільні множини, – довільна підмножини множини ; – довільне відображення. Чи виконується співвідношення
 ?
?Множини , і відображення визначені співвідношеннями:
 .
Чи існує відображення
,
яке є оберненим до
?
.
Чи існує відображення
,
яке є оберненим до
?Чи збігається у просторі послідовність його елементів, для якої
 ?
?Чи збігається у просторі послідовність його елементів, якщо
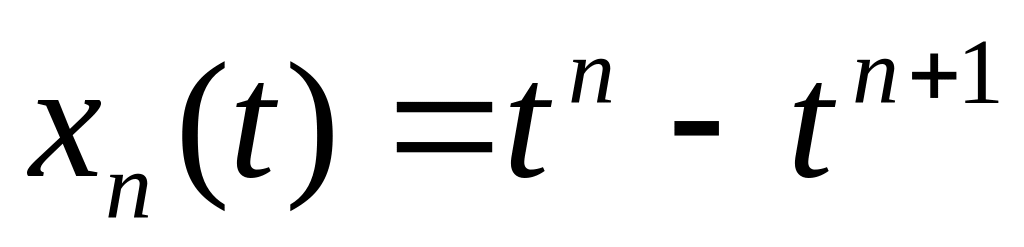 ?
?Чи є множина
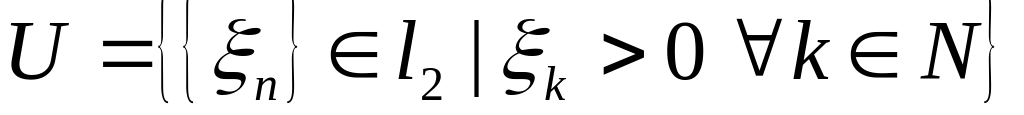 відкритою у просторі
?
відкритою у просторі
?Чи є множина
 замкненою у просторі
?
замкненою у просторі
?Довести, що метричний простір
 є повним.
є повним.
ВАРІАНТ 10
Нехай і – довільні множини,
 – довільна підмножина множини
;
– довільне відображення. Чи виконується
співвідношення
– довільна підмножина множини
;
– довільне відображення. Чи виконується
співвідношення
 ?
?Множини , і відображення визначені співвідношеннями:
 ,
,
 ,
,
 .
Чи існує відображення
,
яке є оберненим до
?
.
Чи існує відображення
,
яке є оберненим до
?Чи збігається у просторі
 послідовність
його елементів, якщо
?
послідовність
його елементів, якщо
?Чи збігається у просторі
 послідовність
його елементів, для якої
послідовність
його елементів, для якої
 ?
?Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина
 замкненою у просторі
?
замкненою у просторі
?Довести, що метричний простір
 є повним.
є повним.
ВАРІАНТ 11
Нехай і – довільні множини, – довільна підмножина множини ; – довільне відображення. Чи виконується співвідношення
 ?
?Побудувати взаємно однозначне відображення множини
 на множину
на множину
 .
.Чи збігається у просторі послідовність його елементів, для якої ?
Чи збігається у просторі послідовність його елементів, якщо
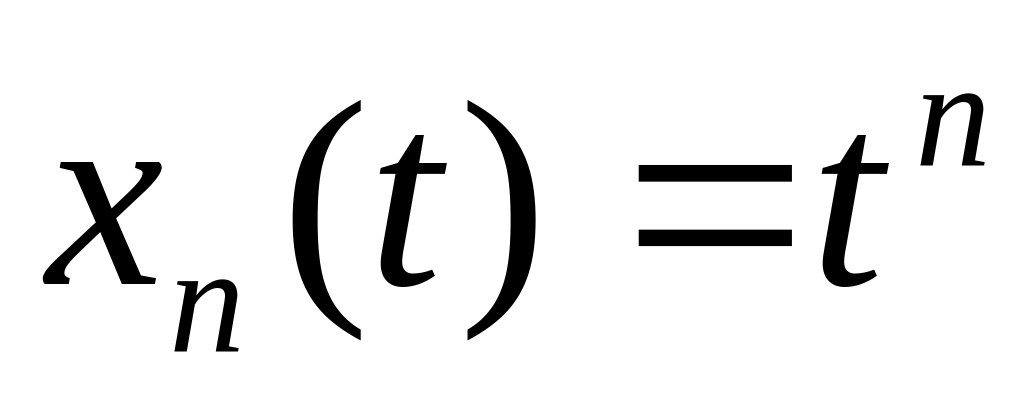 ?
?Чи є множина відкритою у просторі ?
Чи є множина замкненою у просторі ?
На множині
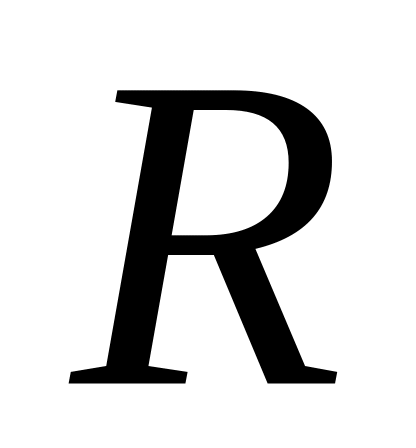 всіх дійсних чисел визначена метрика
всіх дійсних чисел визначена метрика
 .Чи
є отриманий у такий спосіб метричний
простір повним?
.Чи
є отриманий у такий спосіб метричний
простір повним?
ВАРІАНТ 12
Нехай і – довільні множини, – довільна підмножина множини ; – довільне відображення. Чи виконується співвідношення
 ?
?Побудувати взаємно однозначне відображення множини
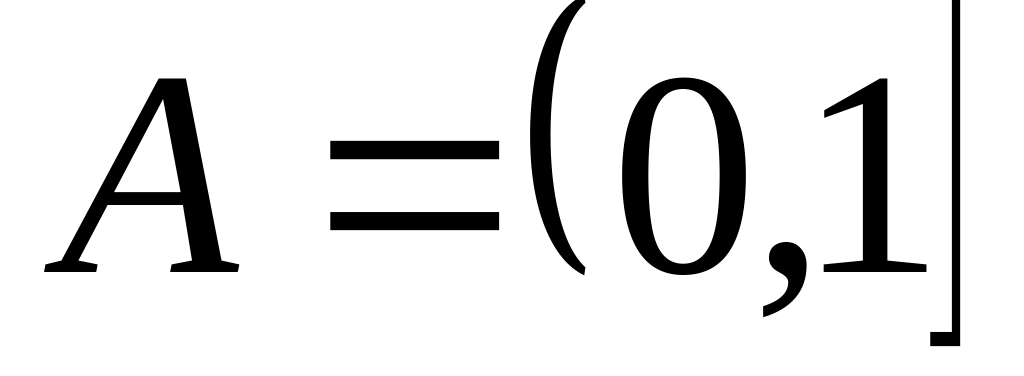 на множину
на множину
 .
.Чи збігається у просторі послідовність його елементів, якщо
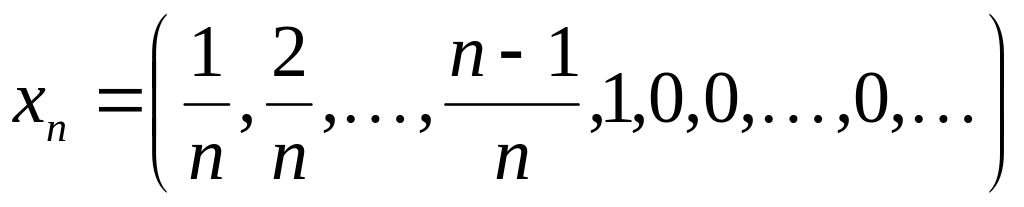 ?
?Чи збігається у просторі
 послідовність
його елементів, якщо
?
послідовність
його елементів, якщо
?Чи є множина відкритою у просторі ?
Чи є множина
 замкненою у просторі
?
замкненою у просторі
?На множині всіх дійсних чисел визначена метрика
 .Чи
є отриманий у такий спосіб метричний
простір повним?
.Чи
є отриманий у такий спосіб метричний
простір повним?
ВАРІАНТ 13
Нехай і – довільні множини, і
 – довільні підмножини множини
;
– довільне відображення. Чи виконується
співвідношення
– довільні підмножини множини
;
– довільне відображення. Чи виконується
співвідношення
 ?
?Побудувати взаємно однозначне відображення множини на множину
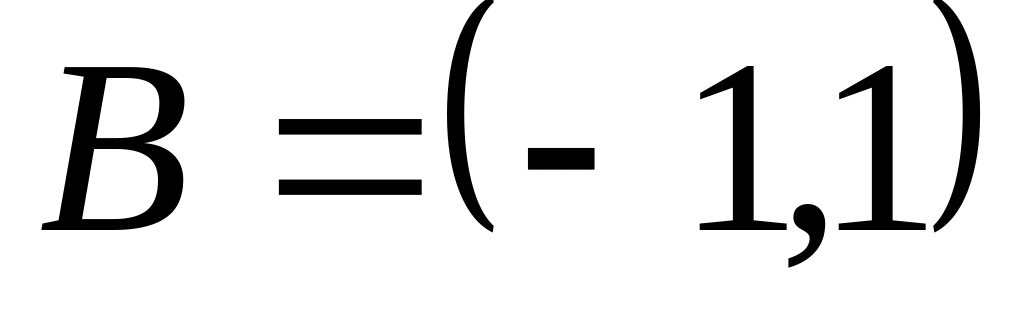 .
.Чи збігається у просторі послідовність його елементів, якщо
 ?
?Чи збігається у просторі
 послідовність
його елементів, якщо
?
послідовність
його елементів, якщо
?Чи є множина відкритою у просторі ?
Чи є множина замкненою у просторі ?
На множині всіх дійсних чисел визначена метрика
 .Чи
є отриманий у такий спосіб метричний
простір повним?
.Чи
є отриманий у такий спосіб метричний
простір повним?
ВАРІАНТ 14
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне відображення. Чи виконується співвідношення
 ?
?Побудувати взаємно однозначне відображення множини
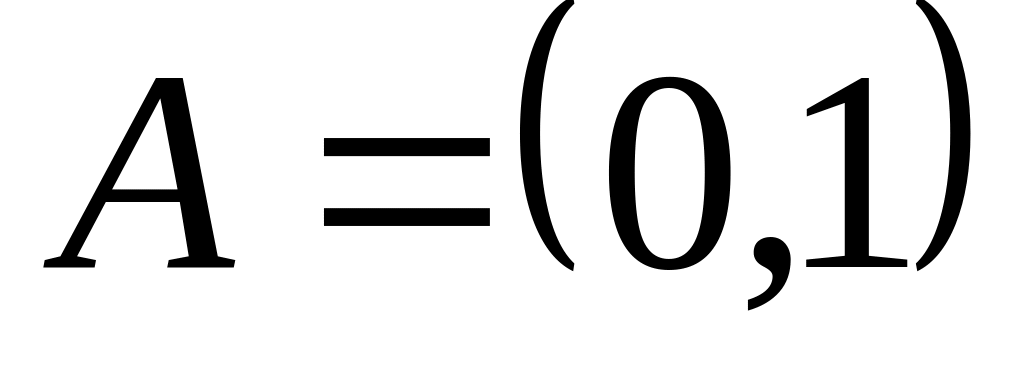 на множину
на множину
 .
.Чи збігається у просторі послідовність його елементів, для якої
 ?
?Чи збігається у просторі
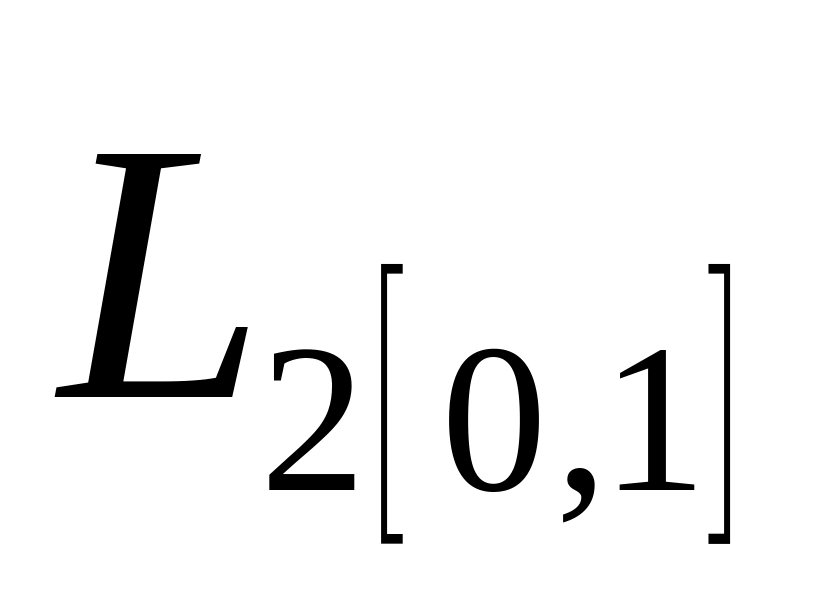 послідовність
його елементів, якщо
?
послідовність
його елементів, якщо
?Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина
 замкненою у просторі
?
замкненою у просторі
?На множині
 всіх додатних дійсних чисел визначена
метрика
всіх додатних дійсних чисел визначена
метрика
 .Чи
є отриманий у такий спосіб метричний
простір повним?
.Чи
є отриманий у такий спосіб метричний
простір повним?
ВАРІАНТ 15
Нехай і – довільні множини,
 і
і
 –
довільні підмножини множини
;
– довільне відображення. Чи виконується
співвідношення
–
довільні підмножини множини
;
– довільне відображення. Чи виконується
співвідношення
 ?
?Побудувати взаємно однозначне відображення множини
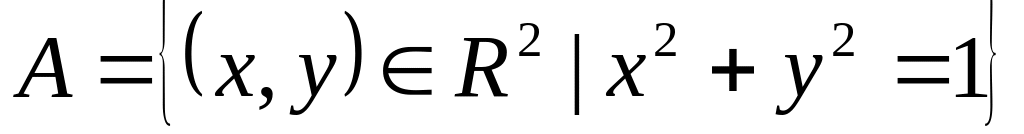 на множину
на множину
 .
.Чи збігається у просторі послідовність його елементів, для якої ,

Чи збігається у просторі послідовність його елементів, якщо ?
Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина
 замкненою у просторі
?
замкненою у просторі
?Довести, що інтегральне рівняння
 має єдиний розв’язок
у просторі
.
має єдиний розв’язок
у просторі
.
ВАРІАНТ 16
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне відображення. Чи виконується співвідношення
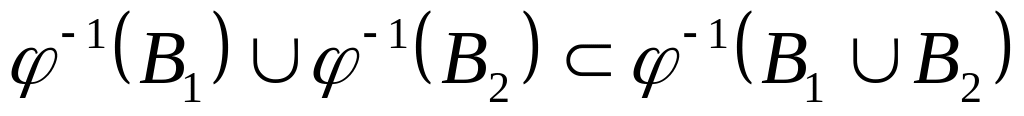 ?
?Побудувати взаємно однозначне відображення множини
 на множину
на множину
 .
.Чи збігається у просторі послідовність його елементів, для якої ,
Чи збігається у просторі послідовність його елементів, якщо ?
Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина замкненою у просторі ?
Довести, що інтегральне рівняння
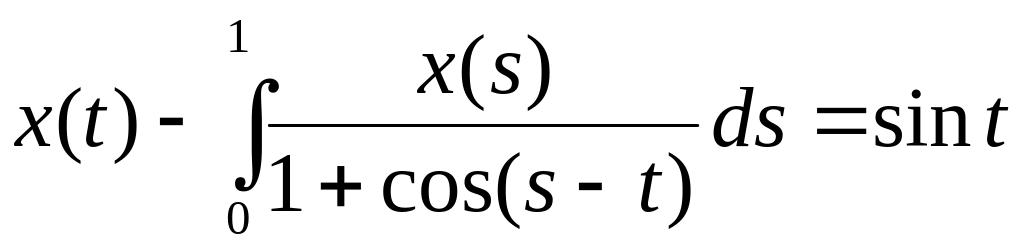 має єдиний розв’язок
у просторі
.
має єдиний розв’язок
у просторі
.
ВАРІАНТ 17
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне відображення. Чи виконується співвідношення
 ?
?Побудувати взаємно однозначне відображення множини на множину .
Чи збігається у просторі послідовність його елементів, для якої ,
Чи збігається у просторі послідовність його елементів, якщо
 ?
?Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина строго зростаючих на відрізку функцій простору замкненою у цьому просторі?
Довести, що інтегральне рівняння
 має єдиний розв’язок
у просторі
.
має єдиний розв’язок
у просторі
.
ВАРІАНТ 18
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне відображення. Чи виконується співвідношення
 ?
?Побудувати взаємно однозначне відображення множини
 на множину
на множину
 .
.Чи збігається у просторі
 послідовність
його елементів, для якої
,
послідовність
його елементів, для якої
,

Чи збігається у просторі послідовність його елементів, якщо ?
Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина неспадних на відрізку функцій простору замкненою у цьому просторі?
Довести, що інтегральне рівняння
 має єдиний розв’язок
у просторі
.
має єдиний розв’язок
у просторі
.
ВАРІАНТ 19
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне відображення. Чи виконується співвідношення
 ?
?Побудувати взаємно однозначне відображення множини
 на множину
на множину
 .
.Чи збігається у просторі послідовність його елементів, для якої ,
Чи збігається у просторі послідовність його елементів, якщо ?
Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина всіх строго зростаючих на відрізку функцій простору замкненою у цьому просторі?
Довести, що інтегральне рівняння
 має єдиний розв’язок
у просторі
.
має єдиний розв’язок
у просторі
.
ВАРІАНТ 20
Нехай і – довільні множини, і
 –
довільні підмножини множини
;
– довільне відображення. Чи виконується
співвідношення
–
довільні підмножини множини
;
– довільне відображення. Чи виконується
співвідношення
 ?
?Побудувати взаємно однозначне відображення множини на множину
 .
.Чи збігається у просторі послідовність його елементів, для якої ,
Чи збігається у просторі послідовність його елементів, якщо
 ?
?Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина всіх неспадних на відрізку функцій простору замкненою у цьому просторі?
Довести, що інтегральне рівняння
 має єдиний розв’язок
у просторі
.
має єдиний розв’язок
у просторі
.
ВАРІАНТ 21
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне відображення. Чи виконується співвідношення
 ?
?Множини , і відображення визначені співвідношеннями:
 ,
,
 .
Чи існує відображення
,
яке є оберненим до
?
.
Чи існує відображення
,
яке є оберненим до
?Чи збігається у просторі послідовність його елементів, для якої ,

Чи збігається у просторі послідовність його елементів, для якої

Чи є множина відкритою у просторі
 ?
?Чи є множина
 замкненою у просторі
?
замкненою у просторі
?Довести, що метричний простір є повним.
ВАРІАНТ 22
Нехай і – довільні множини, і
 – довільні підмножини множини
;
– довільне відображення. Чи виконується
співвідношення
– довільні підмножини множини
;
– довільне відображення. Чи виконується
співвідношення
 ?
?Побудувати взаємно однозначне відображення множини
 на множину
на множину
 .
.Чи збігається у просторі послідовність його елементів, для якої ,
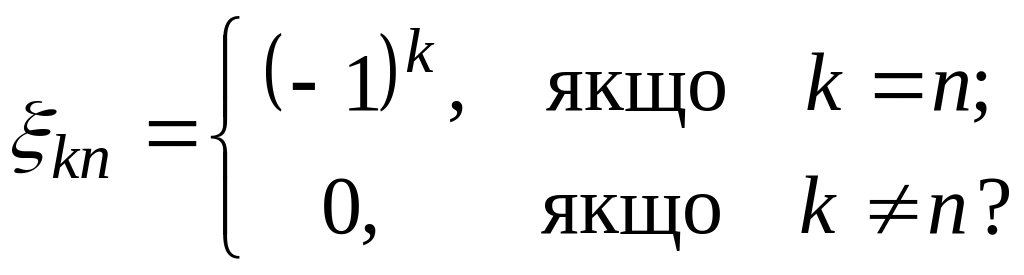
Чи збігається у просторі послідовність його елементів, для якої

Чи є відкрита куля метричного простору відкритою множиною ціого простору?
Чи є відкрита куля метричного простору замкненою множиною ціого простору?
На множині
 визначена метрика
визначена метрика
 ,
де
,
де
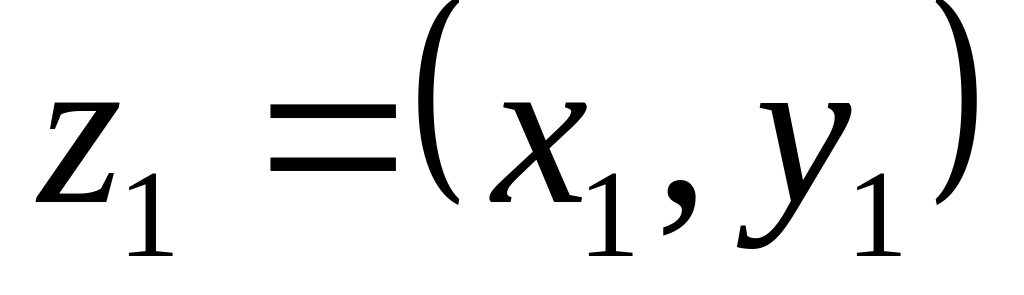 ,
,
 .
Чи є отриманий у такий спосіб метричний
простір повним?
.
Чи є отриманий у такий спосіб метричний
простір повним?
ВАРІАНТ 23
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне взаємно однозначне відображення. Чи виконується співвідношення
 ?
?Побудувати взаємно однозначне відображення множини
 на множину
на множину
 .
.Чи збігається у просторі послідовність його елементів, для якої ,
Чи збігається у просторі послідовність його елементів, для якої
Чи є замкнена куля метричного простору відкритою множиною ціого простору?
Чи є замкнена куля метричного простору замкненою множиною ціого простору?
На множині
 визначена метрика
,
де
,
.
Чи є отриманий у такий спосіб метричний
простір повним?
визначена метрика
,
де
,
.
Чи є отриманий у такий спосіб метричний
простір повним?
ВАРІАНТ 24
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне взаємно однозначне відображення. Чи виконується співвідношення ?
Побудувати взаємно однозначне відображення множини
 на множину
на множину
 .
.Чи збігається у просторі послідовність його елементів, для якої ,
Чи збігається у просторі послідовність його елементів, для якої
Чи є множина
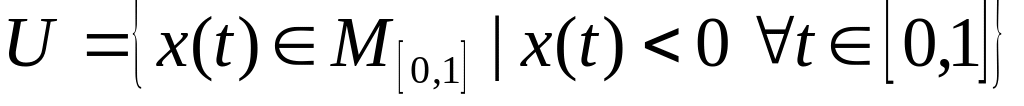 відкритою у просторі
?
відкритою у просторі
?Чи є множина
 замкненою у просторі
?
замкненою у просторі
?На множині
 визначена метрика
визначена метрика
 ,
де
,
де
 ,
,
 .
Чи є отриманий у такий спосіб метричний
простір повним?
.
Чи є отриманий у такий спосіб метричний
простір повним?
ВАРІАНТ 25
Нехай і – довільні множини, і – довільні підмножини множини ; – довільне відображення. Чи виконується співвідношення
 ?
?Побудувати взаємно однозначне відображення множини
 на множину
.
на множину
.Чи збігається у просторі послідовність його елементів, для якої ,

Чи збігається у просторі послідовність його елементів, для якої
Чи є множина
 відкритою у просторі
?
відкритою у просторі
?Чи є множина
 замкненою у просторі
?
замкненою у просторі
?На множині
 визначена метрика
визначена метрика
 .
Чи є отриманий у такий спосіб метричний
простір повним?
.
Чи є отриманий у такий спосіб метричний
простір повним?
