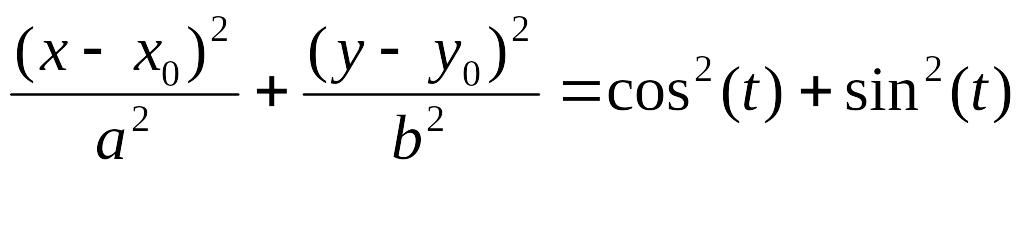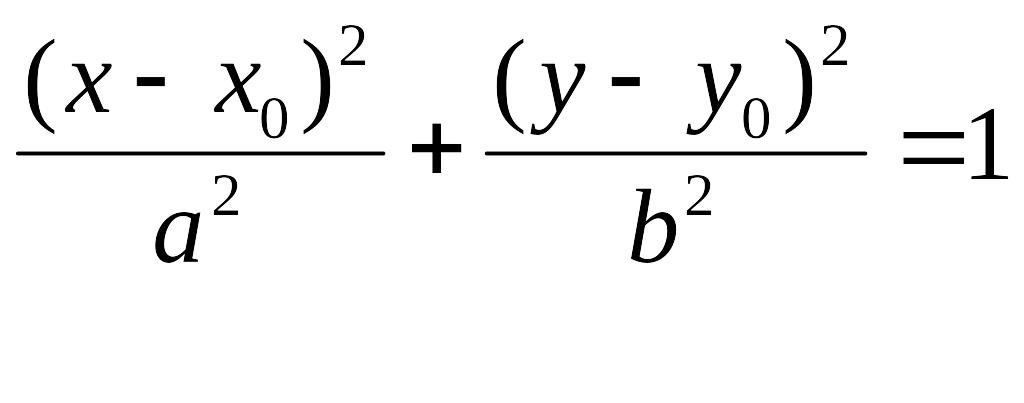3.2. Переход от полярных координат к декартовым.

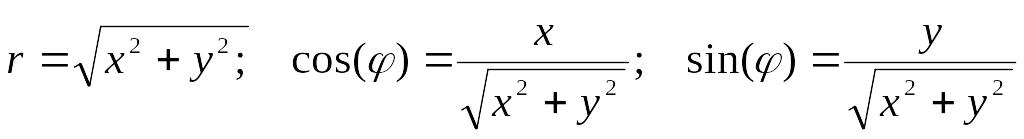
3.4. Параметрически заданные кривые и построение их графиков

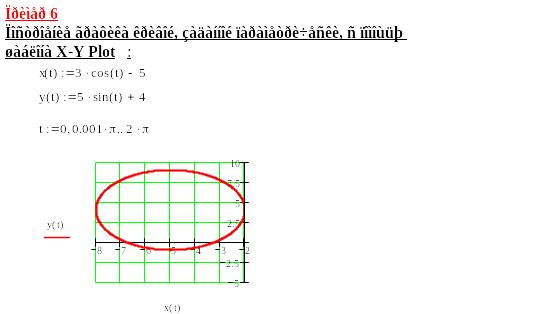
3.4.1. Переход от параметрической записи уравнения к стандартной (в декартовой системе координат)

При переходе от уравнений линий, заданных параметрически, к уравнениям в декартовых координатах, над этими уравнениями необходимо выполнить элементарные преобразования с целью исключения параметра t.

Для иллюстрации рассмотрим преобразования параметрических уравнений эллипса:

Порядок выполнения задания:

Перенесем x0 и y0 в левые части уравнений
Возведем в квадрат левые и правые части уравнений
Разделим обе части 1-го и 2-го уравнений на a2 и b2 соответственно
Суммируем левые и правые части уравнений
Получаем общий вид уравнения эллипса, заданного в декартовых координатах:

3.5. Построение графиков поверхностей

Одним из вариантов построения графика поверхности является вариант применения вращения направляющей линии вокруг какой-либо оси.

Например, построить поверхность конуса, путем вращения направляющей вокруг оси Ох.

 

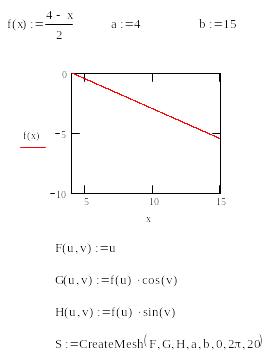
Из примера видно, что для построения графика поверхности таким способом нужно определиться с:

1. 1.      направляющей

2. 2.      правильно задать параметры функции построения CreateMesh.

 

Формат функции выглядит следующим образом:

, где

F, G, H – стандартные функции:

- проекция направляющей f(u) на ось х.

- проекция направляющей f(u) на ось y.

a,b – область определения направляющей функции

mesh – количество направляющих

a, a1 - начало и конец интервала вращения (задается в градусах).

 

После определения функции Createmesh, для построения поверхности нужно выбрать команду

Insert – Graph – Surface Plot.

 

3.5.1 Форматирование графика

Для установки параметров форматирования необходимо выбрать команду Format Graph Surface Plot или щелкнуть по графику два раза левой клавишей мыши.

При этом на экране появится окно форматирования с вложенными вкладками.

На вкладке можно установить следующие параметры форматирования осей X-Y-Z соответственно:

	Прорисовать линии сетки
	Количество линий сетки
	Толщина линий сетки
	Цвет линий сетки
	Нумерация линий сетки
	установка по оси автосетки
	Толщина оси

 

На вкладке General можно установить следующие параметры форматирования графика:

	Поворот
	Масштаб
	Стиль осей

 

На вкладке можно установить следующие параметры форматирования плоскостей графика:

Закрашивание плоскости цветом

 

На вкладке Title можно установить название графика:

3.6. Построение поверхностей многогранников

Polyhedron(S1) – предназначена для построения многогранников.

S1 – может быть:

•      названием многогранника

•      номер кода многогранника

Например,

Polyhedron ("cube") or Polyhedron ("#6") or Polyhedron ("3|2 4")

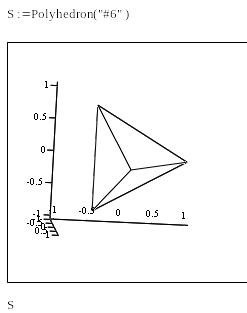
PolyLookup(n) - выводит по коду многогранника его название

Например,