3.3 Построение графиков, заданных в полярной системе координат

Что такое полярные координаты?

Зафиксируем на плоскости точку О и выходящую из нее полупрямую Ор, а также выберем единицу масштаба. Точка О называется полюсом, полупрямая Ор – полярной осью.

Произвольной точке м плоскости поставим в соответствие два числа:

1.       Полярный радиус r, равный расстоянию от точки М до полюса О;

2.       Полярный угол φ, равный углу между полярной осью Ор и полупрямой ОМ. Полярный угол измеряется в радианах. Отсчет положительных и отрицательных значений ведется от Ор против и по часовой стрелке. Полюсу соответствует полярный радиус равный нулю.

Запись М(r; φ) означает: точка М с полярными координатами r и φ.

Зависимость между прямоугольными и полярными координатами следующая:

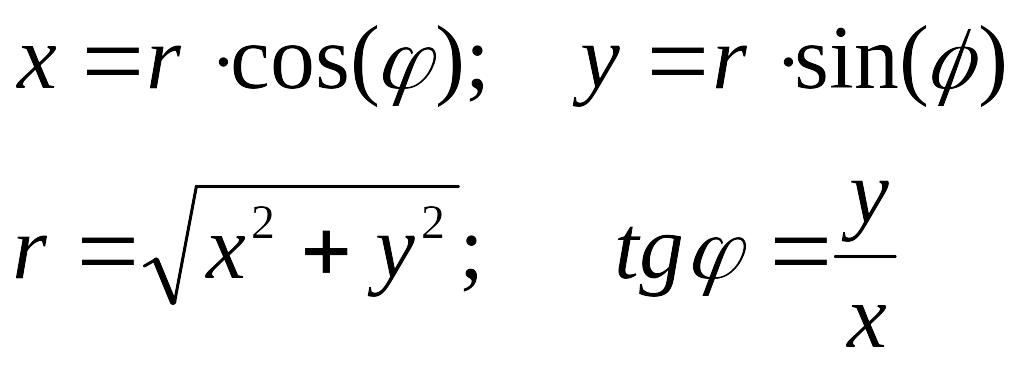
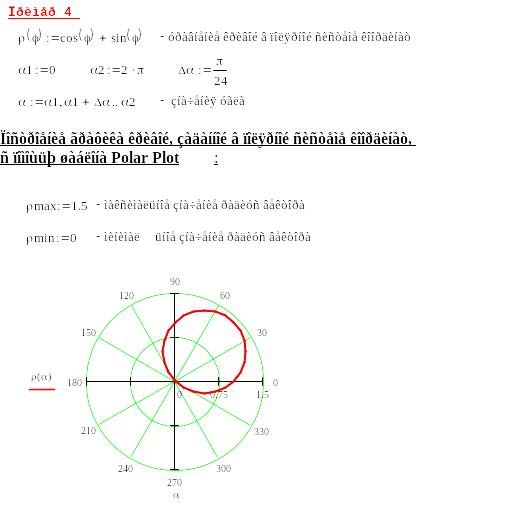
Для построения графика используется шаблон, вызываемый командой:

Insert - Graph - Polar Plot или используется комбинация клавиш Ctrl + 7

После выбора соответствующего шаблона необходимо заполнить его данными:

4.       слева в центральный маркер ввести функцию полярного радиуса

5.       снизу в центральный маркер ввести обозначение полярного угла

6.       нажать на Enter.

Примечание: Для построения на одном графике нескольких функциональных зависимостей нужно ввести соответствующие функции полярного радиуса через запятую.

3.1. Форматирование полярного графика

Для установки параметров форматирования необходимо выбрать команду Format Graph Polar Plot или щелкнуть по графику два раза левой клавишей мыши.

При этом на экране появится окно форматирования с вложенными вкладками.

На первой вкладке можно установить следующие параметры форматирования полярных осей соответственно:

Ось полярного радиуса Radial	Ось полярного угла Angular
установка по оси логарифмической шкалы
установка на оси вспомогательных линий сетки
нумерация оси
установка по оси автосетки
установка по оси режима показа меток
установка по оси размера сетки, в соответствующих текстовых полях
Установка стиля осей
	Выделяет ось полярного радиуса
	выводит график без рамки с осями
	выводит график без рамки и без осей

На второй вкладке можно установить следующие параметры форматирования линии графика:

	название линии графика (trace1 ….)
			dadot - штрих пунктирная линия
	цвет графика
	толщина линии графика (только для линейных)

 

На третьей вкладке можно установить следующие параметры:

заголовок графика:

над графиком       под графиком       вывести заголовок в области графика