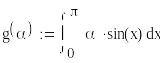Лабораторная работа № 7. Интегральное исчисление в пакете MathCad. Модульное программирование в докуметах MathCad

 

Цель работы: освоение основных приемов вычисление интегралов в пакете MATHCAD, а также использование модульного программирования. (4 часа)

 

Содержание

1. Интегрирование 1

1.1 Понятие неопределенного интеграла 1

1.2 Понятие определенного интеграла 1

1.3 Результат численного интегрирования 3

1.4 О расходящихся интегралах 4

1.5 Кратные интегралы 4

2. Применение интегралов для вычисления площадей и объемов геометрических тел 5

2.1 Вычисление площади фигуры в прямоугольных координатах 5

2.2 Вычисление объема тела вращения 6

2.3 Применение интегралов для вычисления длины дуги кривой 7

2. Численное интегрирование 8

3. Модульное программирование в MathCad 8

3.1. Модульное программирование в одном документа 8

3.2 Модульное программирование в нескольких документах Mathcad 9

 

Индивидуальные задания 11

Задание 1. Вычисление неопределенных интегралов 11

Задание 2. Вычисление определенных интегралов 12

Задание 3. Вычисления площади, длины дуги и объема с помощью определенных интегралов 12

Задание 4. Модульное программирование и численные методы нахождения определенного интеграла. 14

Контрольные вопросы 14

 

1. Интегрирование

1.1 Понятие неопределенного интеграла

Если функция f(x) определена и непрерывна на промежутке (a,b) и F(x) – ее первообразная, то есть F’(x)=f(x) при a<x<b, то

1.2 Понятие определенного интеграла

Если существует предел , не зависящий от способа разбиения отрезка [a;b] и выбора точек , то этот предел будем называть определенным интегралом функции f(x) на отрезке [a;b] и обозначать символом

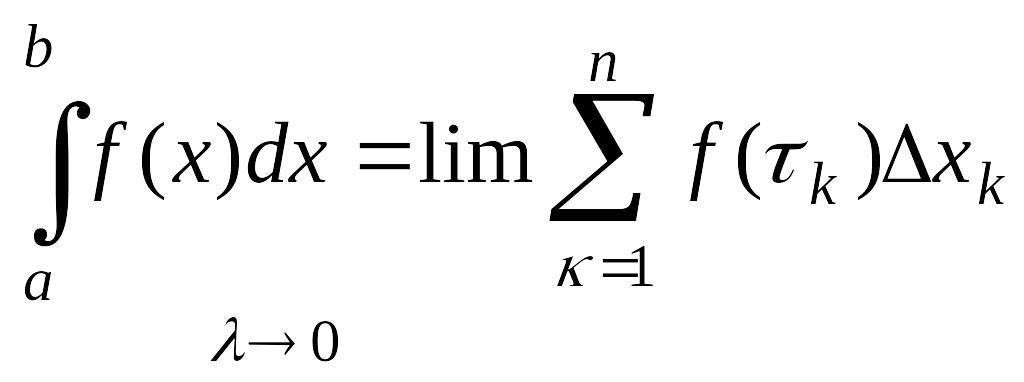
Некоторые свойства определенного интеграла:

•       Определенный интеграл от суммы двух функций равен сумме определенных интегралов от этих функций:

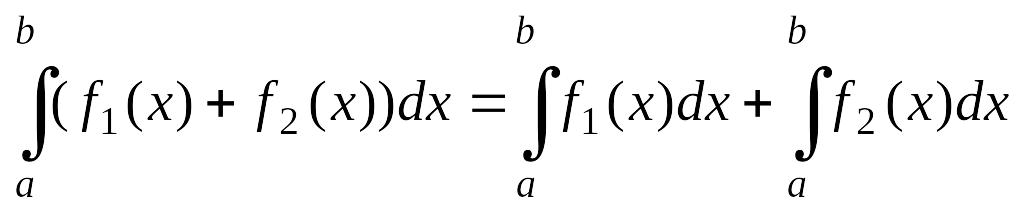
•       При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

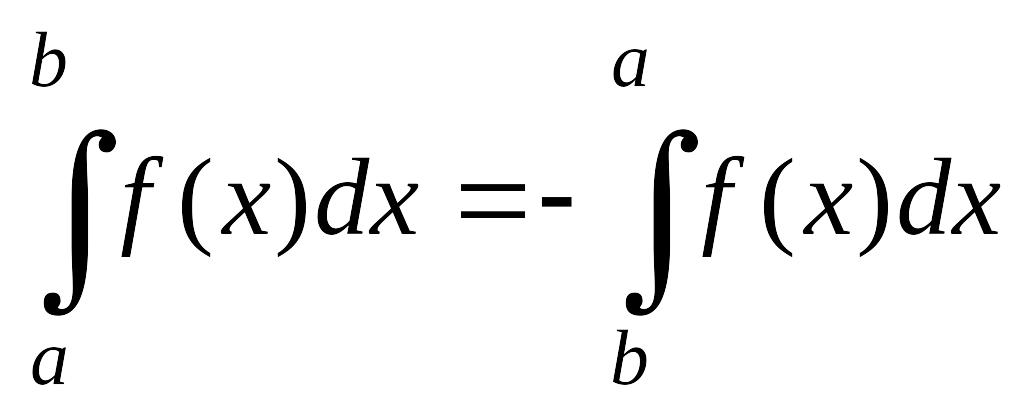
•       Интеграл по отрезку равен сумме интегралов по его частям:

 

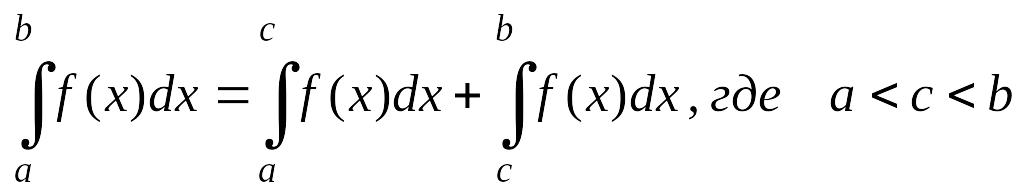
Интегрирование в Mathcad реализовано в виде вычислительного оператора. Допускается вычислять интегралы от скалярных функций в пределах интегрирования, которые также должны быть скалярами. Несмотря на то что пределы интегрирования обязаны быть действительными, подынтегральная функция может иметь и комплексные значения, поэтому и значение интеграла может быть комплексным. Если пределы интегрирования имеют размерность, то она должна быть одной и той же для обоих пределов.

Операторы интегрирования

Интегрирование, дифференцирование, как и множество других математических действий, устроено в Mathcad по принципу "как пишется, так и вводится". Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели Calculus (Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш <Shift>+<7> (или символа "&"). Появится символ интеграла с несколькими местозаполнителями (рисунок 1), в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования.

Можно вычислять интегралы с одним или обоими бесконечными пределами. Для этого на месте соответствующего предела введите символ бесконечности, воспользовавшись, например, той же самой панелью Calculus (Вычисления). Чтобы ввести -> (минус бесконечность), добавьте знак минус к символу бесконечности, как к обычному числу.

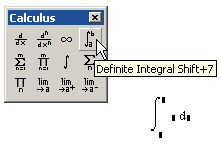
Рисунок 1. Оператор интегрирования

Чтобы получить результат интегрирования, следует ввести знак равенства или символьного равенства. В первом случае интегрирование будет проведено численным методом, во втором — в случае успеха, будет найдено точное значение интеграла с помощью символьного процессора Mathcad. Эти два способа иллюстрирует пример 1. Конечно, символьное интегрирование возможно только для небольшого круга несложных подынтегральных функций.

Пример 1. Численное и символьное вычисление определенного интеграла

Рисунок 2. Численное и символьное вычисление определенного интеграла

 

Подынтегральная функция может зависеть от любого количества переменных. Именно для того чтобы указать, по какой переменной Mathcad следует вычислять интеграл, и нужно вводить ее имя в соответствующий местозаполнитель. Помните, что для численного интегрирования по одной из переменных предварительно следует задать значение остальных переменных, от которых зависит подынтегральная функция и для которых вы намерены вычислить интеграл (пример 2).

Пример 2. Интегрирование функции двух переменных по разным переменным

a:=2	x := 1
Рисунок 3. Интегрирование функции по разным переменным

 

Оператор интегрирования может использоваться точно так же, как и другие операторы: для определения функций, в циклах и при вычислении ранжированных переменных. Пример присваивания пользовательской функции д(х) значения определенного интеграла и вычисления нескольких ее значений приведен в примере 3.

Пример 3. Использование оператора интегрирования в функции пользователя

Рисунок 4. Оператор интегрирования в функции пользователя