Задание 3. Определение экстремумов функции
Для заданной в таблице 3 функции найти экстремумы функции. При определении экстремумов пользоваться правилами на основе определения первой и второй производной.
Таблица 3 – Индивидуальные задания
№ варианта |
Функция |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
Задание 4. Разложение функции в ряд Тейлора
Для заданной функции найти коэффициенты разложения в ряд Тейлора в точке x=a=0, и подтвердить правильность приведенных выкладок.
Таблица 4 – Индивидуальные задания
№ варианта |
Задание |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
;
|
14 |
|
15 |
|
16 |
;
|
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
Задание 5. Решение задачи Коши
Решить заданные в таблице краевые задачи Коши двумя способами: с помощью функции Odesolve() и функции Rkfixed(). Построить полученные решения на одном графике, сравнить результаты и сделать выводы.
Таблица 4 – Индивидуальные задания
№ |
Постановка задачи |
0 |
5x’’(t)+10x’(t)-x(t)=sin(2t) x(0)=1, x’(0)=0 |
1 |
15x’’(t)-x’(t)+x(t)=tg (2t2) x(0)=10, x’(0)=0 |
2 |
X’’(t)-10x’(t)+x(t)=1 x(0)=1, x’(0)=2 |
3 |
2x’’(t)-3x’(t)+x(t)= 2t x(0)=2, x’(0)=1 |
4 |
-x’’(t)+4x’(t)-x(t)=sin(2t) x(0)=1, x’(0)=0 |
5 |
x’’(t)+x’(t)-2x(t)=cos(2t) x(0)=2, x’(0)=5 |
6 |
9x’’(t)-8x’(t)-x(t)=sin(2t) x(0)=1, x’(0)=0 |
7 |
4x’’(t)-10x’(t) =(2t)0.5 x(0)=1, x’(0)=0 |
8 |
x’’(t)-4x’(t)+2x(t)=t2+1 x(0)=1, x’(0)=4 |
9 |
x’’(t)-18x’(t)+6x(t)= 2t+10 x(10)=1, x’(10)=5 |
10 |
3x’’(t)-x’(t)+3x(t)= 2t+sin(t) x(2)=1, x’(2)=0 |
11 |
5x’’(t)+10x’(t)-x(t)=sin(2t2) x(0)=1, x’(0)=-1 |
12 |
5x’’(t)-x’(t)+sin(t)x(t)=2t2 x(0)=4, x’(0)=0 |
13 |
8x’’(t)-x’(t)+17x(t)=t4 x(0)=4, x’(0)=0 |
14 |
12x’’(t)-3x’(t)- x(t)=2t4+1 x(0)=2, x’(0)=-1 |
15 |
-3x’’(t)+4x’(t)-x(t)=sin(2t) x(0)=1, x’(0)=0 |
16 |
x’’(t)+x’(t)-2x(t)=cos(2t) t2 x(0)=2, x’(0)=5 |
17 |
-9x’’(t)-x’(t)+2x(t)=sin(t2) x(0)=1, x’(0)=0 |
18 |
14x’’(t)-10x’(t) =(2t+et)0.5 x(0)=2, x’(0)=0 |
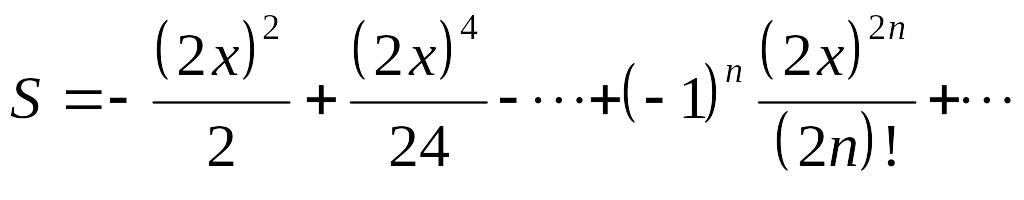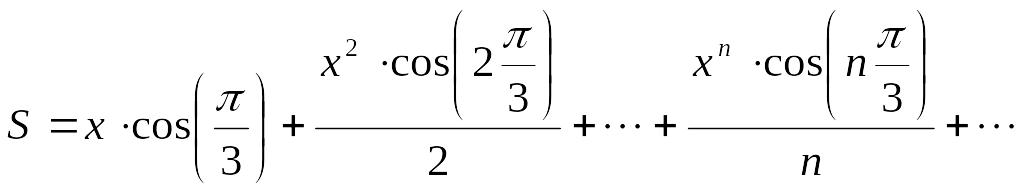