81. Первый закон Фика

Учение об механизме и скорости переноса распред-го в-ва из 1-й фазы во 2-ю назыв кинетикой массооб-х процессов. При этом перенос в-ва в пределах 1-й фазы к границе раздела фаз и обратно наз-ся массоотдача. Перенос в-ва как внутри так и через пов-ть их контакта наз-ся массопередачей. Согласно исследованиям в неподвижных средах в-во переносится только за счет молекулярной диффузии, а в движущихся фазах за счет молекулярной и конвективной диффузий. 1-й з-н Фика: Молекулярная диффузия в газах и жидкостях происх в рез-те хаот-го движения молекул, не связанного с движением газа или жидкости. При мол диф-зии распред-ое в-во m переносится из зоны с высокой в зону с более низкой концентрациейза счет броуковского движ молекул, до достижения равнофазного равновесия . Рассм молекул перенос на упрощ-ой схеме в с-ме г-ж: в фазе G концен-я распр-го компонента выше равновесной следовательно этот компонент перех из г в ж фазу. Выделим 2 элемент-е площади пов-тью dF. Расст-е между ними . На 1-й концентр распр-го компонента- L1, на 2-й-L2 .L1>L2 тогда grad концентр-ии: кинетика переносав этом случае подчиняется 1-му з-ну Фика, который аналогичен з-ну теплопроводности: кол-во продифундирующего в-ва пропор-на градиенту концентр-ии площади перпендикуларной направлению дифуз-го потока и времени. , D- коэф-т молек-ой диф-зии. Способ выражения концентрации и её размерность опр-ют размерность коэф-та диффузии: 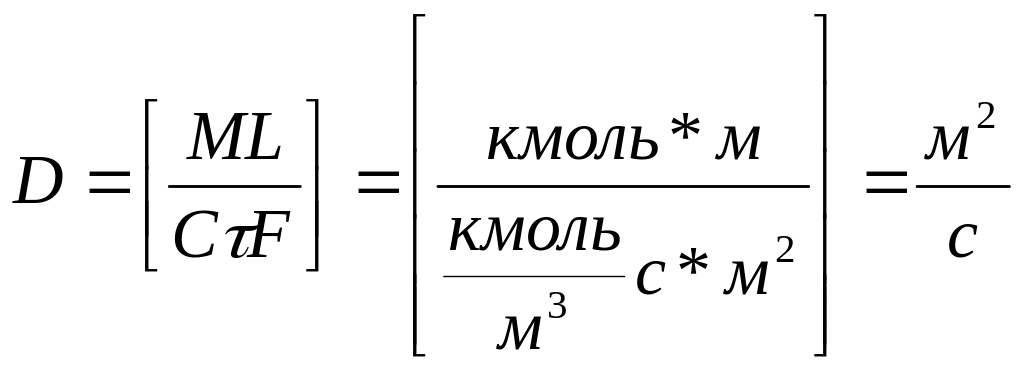Коэф-т молекул-ой диф-ии явл-ся индивидуальным с-вом каждого в-ва.

82. Уравнение конвективного массообмена

Под конвективным массообменом будем понимать суммарный перенос в-ва молекулярной дифф. и молек. переносом. dMa=dM+dMk

Где dM-перенос путем диффузии

dMk-количество в-ва кот переносится конвекцией.

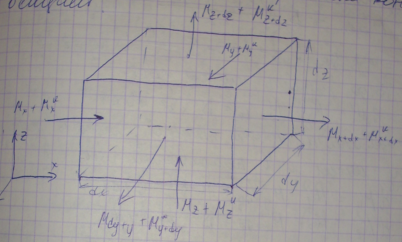
Примем., что процесс массопередачи при установившемся режиме, через С объемную концентр. в-ва, а введем скорости ωх, ωу, ωz.

Тогда масса в-ва, кот. Входит на площадку dzdy(например оси х слева)малекулярная диф-зия за время d𝝉 равна: =

Через новую площадку с учетом изменен. концентрации масса в-ва, кот. выходит из параллелепипеда: М_x+dx=-𝞓 =-𝞓 -𝞓

тогда разн-сть массы сост-т:

Аналогичным образом можно записать разницу массы и в направлении оси Х и Z: ; ;

Тогда полная разность составит:dM=M_x+dM_y+dM_z=𝞓(

Т. о. нашли кол-во вещ-ва, передаваемое за счет молекул. диффузии.За счет конвективного переноса масса в-ва

тогда через правую площадку, учит. что мен-ся концентрация в-ва и скорость:

(С+ (W_x+ dx)

Кол-во в-ва, кот. Выходит из параллелепипеда вдоль оси Х сост-т:

М ^x_x+dx=(

Только разность между началами на входе и выходе сост.:

d

По аналогии решаем для у и z:

d

d

Общее кол-во в-ва в объеме пар-да за время 𝝉 за счет конвективного переноса:

dM^x=d (*)

Для установившегося потока в соответствии с уравнением неразрывности:

=0

C учетом предыд-е выраж-е (*): dM^x=-(ω_{x ,} тогда суммарное изменение массы: dM_a=[d𝞩²c-( ω_x

По закону сохранения массы суммарное изменен массы до л.б.=изменению этой массы во времени: dM_a=

Поскольку в последних уравнениях равны левые части, то приравняем правые части:

ω_x +ω¯proub*с=𝞓𝞩²С - ДУ конвективной диффузии.

Оно выражается значением распределения данного компонента в движущейся стационарной среде при неустановленном процессе массобмена.