22. Основные положения теории Максвелла. Ток смещения. Закон полного тока.
Причиной появления ЭДС индукции в неподвижном контуре является вихревое электрическое поле , она имеет замкнутые линии напряжённости. Работа поля по перемещению заряда по замконутуму контуру отлично от нуля.
Напряжённость
электрического поля: 
, где
- кулоновское электростатическое поле.
Расчитать циркуляцию:
– это уравнение выражает закон
электромагнитное индукции Фарадея и
указывает что изменения магнитного
поля пораждают вихревое электрическое
поле.
Ток смещения:
Плотностью
тока смещения называется вектор:
,
где 
-
вектор электрического смещения.
Ток смещения через произвольную поверхность S равен:
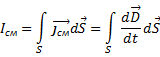
Полный ток.
Плотность
полного тока равна: 
,где 
– плотность тока проводимости.
Полный ток через поверхность S равен:
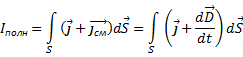
23. Теория Максвелла. Система уравнений Максвелла в интегральной и дифференциальной форме.
Гипотеза Максвелла: Изменение электрического поля приводит к появлению магнитного поля.
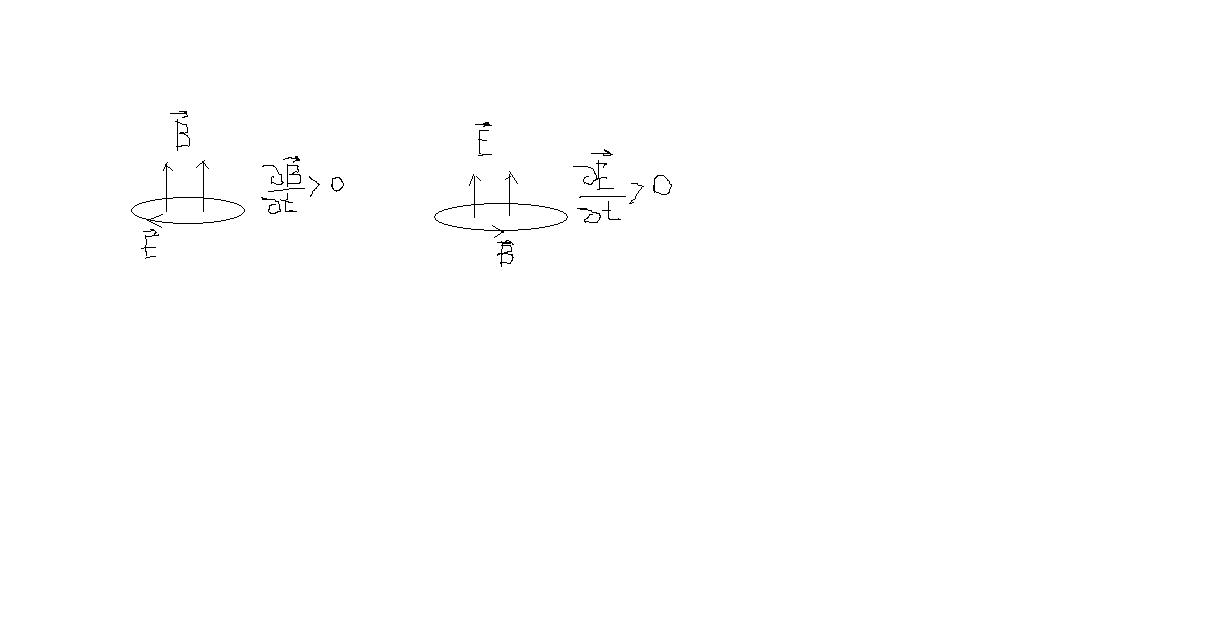
Способностью порождать магнитное поле обладают также проводники с током.
Для результирующей напряжённости поля справедливо уравнение:
Уравнение Максвелла в интегральной форме.
Через произвольную замкнутую поверхность любая линия пройдёт чётное число раз.
Поток
магнитной индукции через замкнутую
поверхность равен нулю: 
-теорема
Гауса для
-устанавливает
связь между током проводимости, током
смещения и циркуляцией магнитного поля
порождённого этими токами.
- линии электр. Индукции могут начинаться
и оканчиваться на зарядах и выражают
теорему Остроградского-Гауса для
Уравнение Максвелла в дифференциальной форме.
По теореме Стокса циркуляция вектора равна потоку его ротора через поверхность ограниченную контуром.
-
верно для любой поверхности. =>
25. Волновое уравнение плоской электромагнитной волны в вакууме и в веществе.
Плоской называется волна с плоскими волновыми поверхностями.
Волновая поверхность – геометрическое место точек расположенных перпендикулярно распространению электромагнитной волны.
Уравнение
для волны распространяющейся вдоль ОХ:
,
где
- величина совершающая колебания.(кси)
-фазовая
скорость.
Из
уравнения Максвелла выводятся уравнения
для 
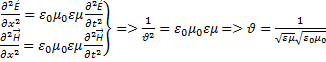
- скорость света в вакууме.
– показатель преломления.
Рассмотрим монохарамотические волны распространяющиеся вдоль оси ОХ:
-волновое число.
Длинна волны λ – расстояние между волновыми поверхностями в которых колебания происходят с фазовым сдвигом 2π т.е. синхронно.
26.Свойства электромагнитных волн. Скорость электромагнитной волны в вакуме и в веществе.
Часные производные
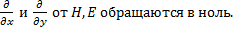
Проекция
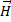на ОХ не содержит переменной компоненты,
а постоянная компонента не является
волной.
Для электромагнитной волны отсутствуют переменные
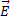направленные вдоль ОХ.Плоская электромагнитная волна является поперечной в изолированном диэлектрике.
В любой точкеволны плотность энергии электрического поля и плотность магнитного поля равны.
- скорость э-м волны в веществе с
показателем преломления n.
– показатель преломления.
- скорость света в вакууме.