13. Ориентация тройки векторов. Векторное произведение векторов. Свойства. Выражение через координаты сомножителей.

Пусть даны три некомпланарных вектора  с общим началом, перечисленных в определенном порядке: первый – , второй – , третий – .

Тройка некомпланарных векторов  называется правоориентированной или просто правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройку векторов называют левой, в этом случае если мы будем смотреть с конца вектора  , то кратчайший поворот от   к   осуществляется по часовой стрелке.

Векторным произведением векторов   и  называется новый вектор  , удовлетворяющий условиям:

1. Д 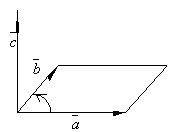лина вектора   равна площади параллелограмма, построенного на векторах   и  .

2. Вектор   перпендикулярен плоскости этого параллелограмма.

3. Он направлен так, что векторы   и   образуют правую тройку векторов.

Векторное произведение векторов   и   обозначается символом  . Если хотя бы один из сомножителей равен нулю, то векторное произведение по определению считают равным нулю.

Векторное произведение обладает следующими свойствами:

1. Из определения следует, что длина векторного произведения численно равна площади параллелограмма, построенного на векторах, и, следовательно, находится по формуле:

.

Таким образом,   и  .

2. При перестановке сомножителей векторное произведение меняет свой знак  .

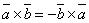Д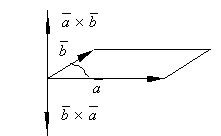 ействительно из определения векторного произведения следует, что векторы   и   имеют одинаковые модули, расположены на одной прямой, но направлены в противоположные стороны. Поэтому, векторы   и   являются противоположными векторами и поэтому  .

3. Скалярный множитель можно выносить за знак векторного произведения, т.е. для любого числа λ и любых векторов 

.

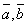
Доказательство этого свойства непосредственно следует из определения векторного произведения. Докажем для λ > 0. В этом случае  . Тогда по определению векторного произведения

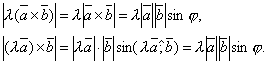
Вектор   перпендикулярен векторам   и  . Вектор   также   векторам   и  , т.к. векторы   и  ,   и   лежат в одной плоскости. Следовательно, векторы   и   коллинеарны. Очевидно, что направления их также совпадают. Т. к.  , и следовательно,  , то  .

Поэтому  .

Аналогично проводится доказательство для случая λ < 0.

4. Для любых векторов   имеет место равенство

.

Примем без доказательства.

5. Векторное произведение двух векторов равно нулевому вектору тогда и только тогда, когда один из сомножителей равен нулю или векторы коллинеарны.

Действительно, если векторы коллинеарны, то  , т.е. площадь параллелограмма, построенного на данных векторах,равна нулю.

Таким образом, для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.

В частности  .

14. Смешанное произведение векторов. Геометрический смысл. Свойства. Выражение через координаты сомножителей.

Смешанным произведением трёх векторов   называют число, равное  . Обозначается  . Здесь первые два вектора умножаются векторно и затем полученный вектор   умножается скалярно на третий вектор  . Очевидно, такое произведение есть некоторое число.

Рассмотрим свойства смешанного произведения.

1. Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е.  .

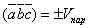Таким образом,   и  .

Д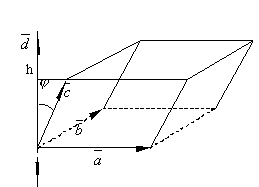 оказательство. Отложим векторы   от общего начала и построим на них параллелепипед. Обозначим   и заметим, что  . По определению скалярного произведения

. Предполагая, что   и обозначив через h высоту параллелепипеда, находим  .

Таким образом, при 

Если же  , то   и  . Следовательно,  .

Объединяя оба эти случая, получаем   или  .

Из доказательства этого свойства в частности следует, что если тройка векторов   правая, то смешанное произведение  , а если   – левая, то  .

2. Для любых векторов  ,  ,   справедливо равенство

.

Доказательство этого свойства следует из свойства 1. Действительно, легко показать, что   и  . Причём знаки "+" и "–" берутся одновременно, т.к. углы между векторами   и   и   и   одновременно острые или тупые.

3. При перестановке любых двух сомножителей смешанное произведение меняет знак.

Действительно, если рассмотрим смешанное произведение  , то, например,   или

.

4. Смешанное произведение 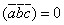  тогда и только тогда, когда один из сомножителей равен нулю или векторы   – компланарны.

Доказательство.

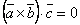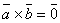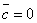1. Предположим, что  , т.е.  , тогда   или   или  .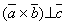

Если  , то   или   или  . Поэтому   – компланарны.

Если  , то  ,  ,   - компланарны.

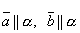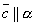2. Пусть векторы   – компланарны и α – плоскость, которой они параллельны , т. е.   и  . Тогда 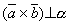 , а значит  , поэтому 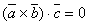  или  .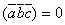

Т.о., необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения. Кроме того, отсюда следует, что три вектора   образуют базис в пространстве, если  .

Если векторы заданы в координатной форме  , то можно показать, что их смешанное произведение находится по формуле:

.

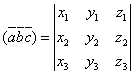Т. о., смешанное произведение  равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.

15. Понятие об уравнении линии и поверхности. Алгебраические линии и поверхности, их порядок.

Определение. Cвязь y = f(x) или F(xy) = 0 называется уравнением линии L, если этим соотношениям удовлетворяют координаты любой точки линии L и не удовлетворяют координаты точек, не принадлежащих линии L.

Таким образом, координаты на плоскости позволяют для каждой линии выписать некоторое уравнение, которое определяется геометрическими свойствами линии, кроме того, оказывается, что каждому уравнению можно поставить в соответствие некоторую линию, и только координаты точек этой линии будут удовлетворять данному уравнению. В связи с этим возникают две задачи.  1. По геометрическим свойствам линии требуется составить ее уравнение.  2. По некоторому уравнению требуется установить геометрические свойства линии, которая этим уравнением определяется.

Эти две задачи и составляют предмет аналитической геометрии на плоскости.

Если взять трехмерное пространство, то к таким геометрическим объектам, как пространственные линии, добавляются новые геометрические объекты - поверхности в трехмерном пространстве.

Поскольку положение точки в пространстве определяется тремя координатами x, y, z, то и условие, которому удовлетворяют все точки, принадлежащие данной поверхности, аналитически выражается уравнением F(x, y, z) = 0.

Определение. Уравнение поверхности есть уравнение F(x, y, z) = 0, которому удовлетворяют координаты всех точек данной поверхности, и притом только этих точек.

Пространственные линии можно рассматривать как линии пересечения некоторых поверхностей. На случай трехмерного пространства легко перефразируются указанные выше две задачи, которые и будут составлять предмет аналитической геометрии в пространстве. В дальнейшем, множество всех точек плоскости будем обозначать как двумерное пространствоR², а трехмерное пространство - как пространство R³ .

Определение. Поверхность называется алгебраической, если в некоторой прямоугольной декартовой системе координат она определяется уравнением 

F(x, y, z) = 0 

где F(x, y, z) - целый многочлен относительно переменных x, y, z.

Степень этого многочлена относительно x,y,z называется порядком алгебраической поверхности. Так, например, 3x - 2y + 5z - 2 = 0 есть алгебраическая поверхность первого порядка, (x - 2)2 + (y + 3)2 + (z - 5)2 = 32 есть алгебраическая поверхность второго порядка.

Определение. Всякая неалгебраическая поверхность называется трансцендентной.

16. Прямая линия на плоскости как линия 1-го порядка. Различные виды уравнения прямой плоскости (общее, векторное‚ векторно-параметрическое, каноническое, с угловым коэффициентом). Расстояние от точки до прямой.

Определение. Уравнение вида

F(x,y)=0 (1)

называется уравнением линии L в заданной системе координат, если этому удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

Степень уравнения (1) определяет порядок линии. Будем говорить, что уравнение (1) определяет (задает) линию L.

Определение. Уравнение вида

Ах+Ву+С=0 (2)

при произвольных коэффициентах А, В, С (А и В одновременно не равны нулю) определяют некоторую прямую в прямоугольной системе координат. Данное уравнение называется общим уравнением прямой.

Уравнение (2) есть уравнение первой степени, таким образом, каждая прямая есть линия первого порядка и, обратно, каждая линия первого порядка есть прямая.

Уравнение прямой с угловым коэффициентом.

Пусть дано уравнение Ах+Ву+С=0 при условии, что коэффициент В не равен нулю. Выполним следующие преобразования

, 

k= tg α – угловой коэффициент.

Если b=0 то прямая проходит через начало координат. Уравнение примет вид

Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох.

Если α=π/2, то уравнение теряет смысл. В этом случае уравнение примет

вид и пройдет

параллельно оси оу.

Параметрические уравнения прямой.

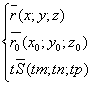
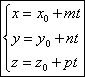
Канонические уравнения прямой.

S(m;n;p) – направляющий вектор прямой L. M₀(x₀;y₀

;z₀) – точка на прямой.

соединяет M₀ с произвольной точкой М.

Уравнение прямой в пространстве, проходящей через две точки.

M₁(x₁;y₁;z₁) M₂(x₂;y₂;z₂)

В качестве направляющего вектора можно задать вектор

Следовательно:

, тогда

 Расстояние от точки до прямой определяется длиной перпендикуляра, опущенного из точки на прямую.