8. Постоянный электрический ток. Вектор плотности тока. Законы Ома и Джоуля ленцза в дифференциальной форме.
Электрическим током называют упорядоченное движение заряженных частиц или заряженных макроскопических тел. Различают два вида электрических токов – токи проводимости и конвекционные токи.
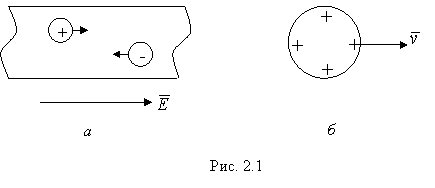
Током проводимости
называют упорядоченное движение в
веществе или вакууме свободных заряженных
частиц – электронов проводимости (в
металлах), положительных и отрицательных
ионов (в электролитах), электронов и
положительных ионов (в газах), электронов
проводимости и дырок (в полупроводниках),
пучков электронов (в вакууме). Этот ток
обусловлен тем, что в проводнике под
действием приложенного электрического
поля напряженностью
происходит
перемещение свободных электрических
зарядов (рис. 2.1, а).
Плотностью
тока
называют
векторную физическую величину, совпадающую
с направлением тока в рассматриваемой
точке и численно равную отношению силы
тока dI, проходящего через элементарную
поверхность, перпендикулярной направлению
тока, к площади этой поверхности:
(2.2)
Единица плотности тока – ампер на
квадратный метр (А/м2).
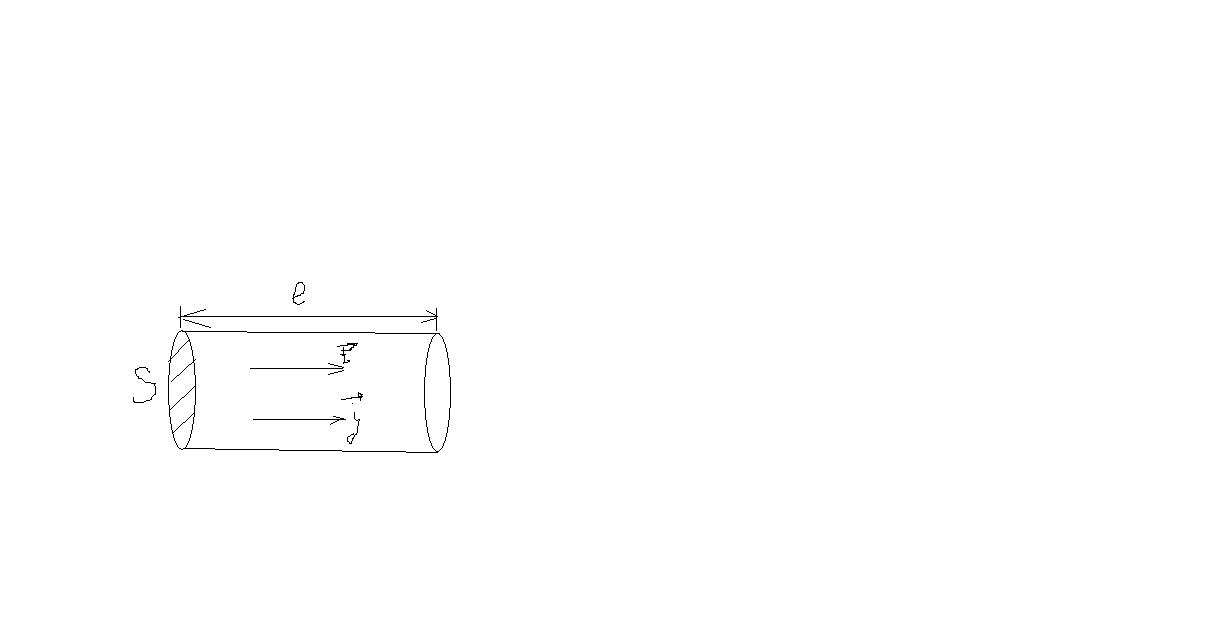
Плотность постоянного электрического
тока одинакова по всему поперечному
сечению однородного проводника. Поэтому
для постоянного тока в однородном
проводнике с площадью поперечного
сечения S сила тока равна
Закон Ома в дифференциальной форме
Если 
то 
– закон Ома в дифференциальной форме.
-закон Ома в обычной форме.
Закон Джоуля-Ленца в дифференциальной форме. Расчитаем работу по перемещению заряда из точки в в точку с :
Удельная мощность тока.
показывает
какое кол – во теплоты выделяется за
единицу времени – закон в дифф. Форме.
– закон в обычной форме.
9. Магнитное поле в вакууме. Магнитное взаимодействие токов. Сила Ампера. Магнитная индукция.
Магнитное поле в вакууме.
Магнитное поле называется компонентой электромагнитного поля, которая создаётся движущимися зарядами и действует на движущиеся заряды.
Магнитное поле – это физический объект – переносчик магнитного взаимодействия.
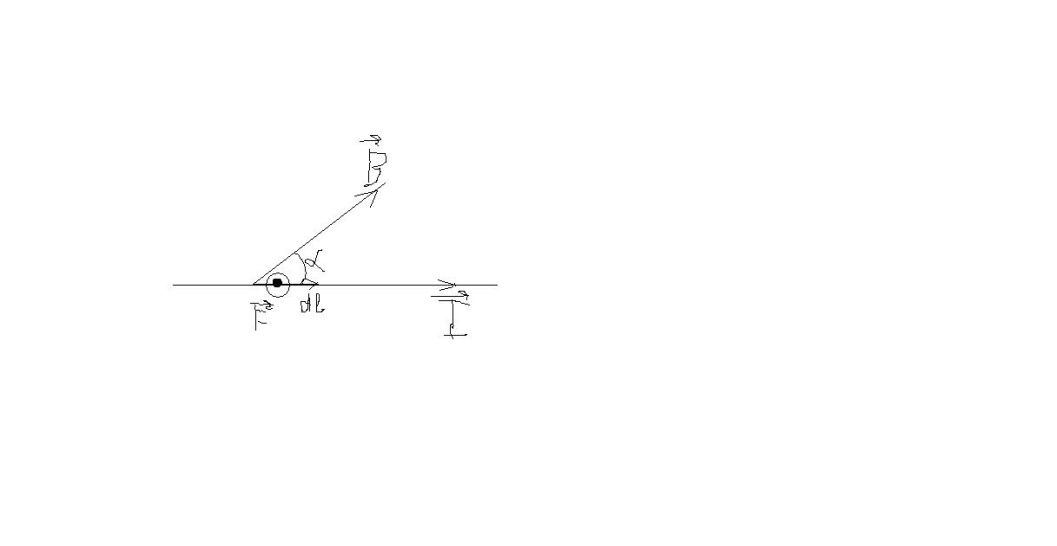
Со стороны магнитного поля на проводники с током действует сила Ампера.
– сила Ампера действующая на проводник
с током.
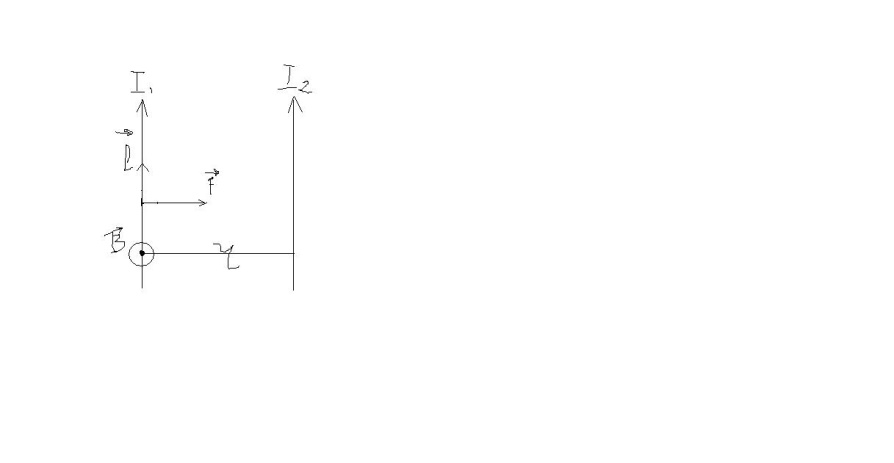
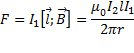
Если
l=r=1m ,
,
то F=2*10^-7 H. На этом основано определение
единицы силы тока.
10. Закон Био-Савара-Лапласса в дифференциальной форме. Расчёт магнитного поля в центре кругового тока и на оси кругового тока.
Магнитная индукция создаётся элементом Idl и определяется законом Био-Савара-Лапласа.
- Закон б-с-л.
Магнитное поле, силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения. М. п. характеризуется вектором магнитной индукции В, который определяет: силу, действующую в данной точке поля на движущийся электрический заряд
Расчет магнитного поля в центре кругового тока и на оси кругового тока:
расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле
где R – радиус кругового проводника.
Для определения направления вектора
также можно использовать правило
буравчика, только теперь его рукоятку
нужно вращать в направлении кругового
тока, а поступательное перемещение
буравчика укажет направление вектора
магнитной индукции.
Расчет магнитного поля на оси кругового тока:
