
Глава I. Основания дискретной математики.
I.I Множества.
В математике понятие “множество” является исходным и не подлежит точному определению. Поэтому набор или совокупность каких-либо объектов, обладающих общими свойствами, на интуитивном уровне, называют множеством. Например, в математике такими множествами являются множество целых чисел Z (INTEGER), множество вещественных чисел R (REAL) и др. “Нематематические” объекты также формируют множества: множество клавиш клавиатуры персонального компьютера (keyboard) - А, множество команд операционной системы компьютера (executive instruction) - В и др.
Объекты, включаемые в множество, называют его элементами. Например, число “3” есть элемент множества Z, клавиша “enter” - элемент множества A, команда “copy” - элемент множества В.
Общим обозначением множества служит пара фигурных скобок {, }, между которыми перечисляют все элементы множества или указывают свойства, которыми должны обладать элементы формируемого множества. Для обозначения множества в тексте используют прописные буквы латинского алфавита A, B, C, ...X, Y, Z, иногда эти же буквы, но с нижними индексами из множества натуральных чисел ( например, A1, ...X12 и т.д.). Для обозначения элементов множества в тексте используют строчные буквы латинского алфавита a, b, c,...x, y, z, иногда эти же буквы, но с нижними индексами из множества целых положительных чисел ( например, a1, ...x12и т.д.).
Для обозначения принадлежности элемента x множеству X используют знак ““ - знак принадлежности, т.е. xX. Если элемент х не принадлежит множеству Х, то используют знак ““, т.е. хХ.
Например, 0Z, 12.5R,escA,cdA,breakB. Множество, каждый элемент которого может приобрести индекс из множества натуральных чисел N={1,2,... n} называют счетным. Если n конечно, то множество называют конечным.
Число элементов счетного конечного множества Х называют его мощностью и обозначают так: |X|=n.
Например, для множества клавиш клавиатуры персонального компьютера A={esc;f1;f2; ...;;inc;del;enter} мощность этого множества |A|=102, для множества команд операционной системы MS DOS персонального компьютера B={break;cd;cls; ...;sys;tree;xcopy} мощность этого множества |B|=61.
Если всякий элемент множества Х является также элементом другого множества Y, то множествоXназывают подмножеством множества Y. Для обозначения этого в тексте используют знак ““ - знак включения, т.е. ХY. Если множество Х не включено в множество Y, т.е. не все его элементы принадлежат Y, то используют знак ““ - знак невключения, т.е. XY.
Например, множество клавиш клавиатуры персонального компьютера содержит подмножество алфавитно-цифровых клавиш и клавиш со знаками пунктуации - A1 и подмножество специальных клавиш, предназначенных для исполнения специальных функций (ввод строчных или прописных букв, смена алфавита, ввод или удаление символа и т.п.) - А2. При этом А1А и А2А, а мощности множеств А1 и А2 равны |А1|=46 и |А2|=56. Множество команд операционной системы MS DOS включает в себя два подмножества команд: внутренние и внешние. Подмножество внутренних команд В1 выполняется самим командным процессором MS DOS. Мощность этого множества равна |B1|=27. Подмножество внешних команд В2 - это программы, поставляемые вместе с операционной системой в виде отдельных файлов. Мощность этого множества равна |B2|=34.
Если XY и YX, то X=Y.
Если Xи XY, то множество Х называют собственным подмножеством множества Y. Для указания в тексте этого факта используют знак строгого включения - ““, т.е. XY.
Например, А1А или В1В.
Множество, не содержащее ни одного элемента, называют пустым множеством и обозначают знаком , т.е.={ }. Пустое множество может быть подмножеством любого множества.
Множество, содержащее все элементы всех подмножеств, принимающих участие в решении какой-либо задачи, называют основным или универсальным множеством и обозначают символом U, т.е. если в решении какой-либо задачи принимают участие множества А={a} и B={b,c}, тоU={a,b,c}.
Максимально возможное число подмножеств универсального множества называют семейством подмножеств универсального множества. Это семейство включает пустое подмножество, само универсальное множество и множества, сформированные по одному, два, три и т.д., элементов универсального множества. Формирование выборок по одному, два, три и т.д. элементов реализуется процедурой комбинаторики - сочетанием ( об этом подробнее см 2.5). Семейство подмножеств универсального множества обозначают символомB(U) и называют булеаном множестваU(см. также 2.8.).
Например, если U={a,b,c},B(U)={, {a}, {b}, {c}, {a,b}, {b,c}, {a,c}, {a,b,c}}.
Легко видеть, что число элементов булеана B(U) зависит от числа элементов универсального множестваU по формуле: |B(U)|=2|U|.
Например, если |U|=3 имеем |B(U)|=23=8.
Число элементов булеана B(U)-есть его мощность |B(U)|.
Задание множества может быть выполнено перечислением элементов внутри фигурных скобок, либо описанием его характеристических свойств.
При задании множества описанием его характеристических свойств между фигурными скобками после указания текущего значения элемента множества Х, т.е. хХ, ставится знак ““, вслед за которым указывают характеристическое свойство элементов множества, т.е. Р(х). При подстановке конкретного значения х=а выражение Р(а) принимает значение “истина” или “ложь”, т.е. Р(х) есть логическая функция, которую иначе называют-“предикат”.
Множество значений х=а1, х=а2, х=а3 и т.д., для которых Р(х=аi)=“истина” формирует множество Х={а1, а2, а3,...}.
Например,
а) если Z={n|P(n):- “быть целым положительным числом”}, то Z={1;2;3;...;n};
б) если А={a|P(a):- “быть клавишей клавиатуры компьютера”}, то А={esc;f1;f2; ...;inc;del; enter};
в) если В={b|P(b):-”быть командой операционной системы персонального компьютера”}, то B={break;cd;copy;...;tree; xcopy}.
Для работы на компьютере цифровые данные определены типом данных. Простейшими стандартными типами данных являются INTEGER - множество целых чисел, REAL - множество вещественных чисел, BOOLEAN - множество логических значений, CHAR - множество символов и др. При указании типа данных обязательно следует указывать границы множества. Формы и способы этих ограничений различны для различных алгоритмических языков.
Если даны два множества Х и Y, то множество всех упорядоченных пар (x;y), где хХ и yY, называют прямым произведением множеств Х и Y и обозначают (XY)., т.е. (XY)={(x,y)|xX, yY}
Аналогично прямым произведением нескольких множеств X1, X2,...,Xnназывается множество всех упорядоченных последовательностей (x1; x2; ...;xn), таких что x1X1x2X2... xnXn. Прямое произведение X1, X2,...Xn принято обозначать (X1X2...Xn) или i=1n Xi, т.е. (X1X2...Xn)={(x1,x2,...xn)| x1X1, x2X2, ..., xnXn}.
Если одно из множеств произведения пусто, то пусто и все прямое произведение, т.е. если Xi=, то X1X2...Xi...Xn=.
Если X1=X2=...=X, то прямое произведение обозначают такi=1n Xiили так Xn.
Упорядоченный набор элементов (x1; x2; ...; xn) называют кортежем, а каждый его элемент - компонентой кортежа. Число компонент кортежа n определяет его длину или ранг. Для обозначения кортежа будем использовать круглые скобки. Длина пустого кортежа равна нулю. Кортежи длины n>1 называют n-кой (двойкой, тройкой, и т.д.).
Два кортежа, имеющих одинаковую длину и одинаковые имена компонент, но различные их значения, называют совместимыми кортежами.
Два кортежа, имеющих одинаковую длину, одинаковые имена и одинаковые значения компонент, равны друг другу.
При обработке данных на компьютере прямое произведение множеств широко используют в формировании составных типов данных. Например, на алгоритмическом языке Фортран предложение INTEGER*2VECT(10) описывает составное данное (кортеж) с именем VECT, содержащим 10 компонент типа INTEGER, причем для каждой компоненты в памяти выделено поле размером 2 байта.
В базах данных такой кортеж называют записью(record).
Заданное множество кортежей всегда является подмножеством прямого произведения множеств, т.е.
{(x1; x2;...; xn)| x1X1, x2X2, ...,xnXn}(X1X2...Xn).
Например, если X1={a;b;c;d;e;f;g;h} и X2={1;2;3;4;5;6;7;8}, то прямое произведение этих множеств формирует 64 кортежа (x1,x2), однозначно определяющих каждую клетку шахматной доски, т.е. (X1X2)={(a;1);(a;2);...(h;7);(h;8)}.
Если известны мощности множеств |X1|=m1, |X2|=m2, ... |Xn|=mn, то мощность произведения |X1X2...Xn|=m1m2...mn, что определяет максимальное число кортежей.
Проекцией кортежа на i-ую компоненту называется его i-ая компонента, что принято обозначать так:
Прi(x1;x2;...xi;...xn)=(xi)
Проекцией кортежа на i-ую, j-ую,m-ую компоненты называется кортеж, компоненты которого принимают значения i-ой, j-ой,m-ой компонент исходного кортежа, что принято обозначать так:
Прi;j;...m(x1;x2;...xi;...xj;...xm;...xn)=(xi;xj;...xm).
Контрольные вопросы и задачи.
I. Верно ли, что
а){1;2}{{1;2;3};{1;3};1;2};
б){1;2}{{1;2;3};{1;3};1;2};
в) если АВ и ВС, то АС;
г) если АВ и ВС, то АС;
д) если А1А2А3...АnА1, то А1=А2=А3=...=Аn
2. Перечислите элементы множества
а) Х={х|Р(х):-(х2-7х+6=0)};
б) Х={х|Р(х):-(х2-1=0)};
3. Приведите примеры таких множеств А, В, С, для которых справедливо
а) АВ, ВС, АС;
б) АВ, ВС; АС;
4. Выписать элементы множества
а) ({1;2}{2;3;4});
б) ({1;2}{3;4});
5. Найти проекции кортежей
а) Пр2,3(х1;х2;х3);
б) Пр1,3,5(х1;х2;х3;х4;х5);
6. Верно ли, что А=В, если
а) А={2;5;4}, B={5;4;2};
б) A={1;2;4;2}, B={1;4;2};
в) A={2;4;5}, В={2;4;3};
г) F={1;{2;5};6}, D={1;{5;2};6};
7. Приняв множество первых 20 натуральных чисел в качестве универсального множества, записать следующие его подмножества: А- множество четных чисел, В- множество нечетных чисел, С- множество квадратов чисел, D- множество простых чисел.
I.2. Соответствия. Отображения. Отношения.
Если элементы двух множеств X и Y различной природы сопоставить между собой по какому-либо правилу, т.е. для каждого хХ указать один или несколько элементов множества Y, то может быть сформировано множество пар (х;y), являющееся подмножеством прямого произведения множеств Х и Y, т.е.
{(x;y)|xX, yY}(XY).
Множество Х чаще всего называют областью отправления, а множество Y-областью прибытия. Значение yY называют образом для конкретного значения хiХ, а значение хХ - прообразом для конкретного значения yjY.
Соответствия.Сопоставление двух множеств Х и Y, когда для каждого элемента хiХ существует несколько образов, т.е. |{y}xi|>1, называют соответствием. Множество пар (x;y) соответствия обозначают Q, т.е.
Q={(x;y)|xX, yY}(XY).
Правило соответствия удобно записать в операторной форме q:XY, где q-оператор соответствия.
Наиболее ярким представителем соответствия является словарь, например, англо-русский, т.к. одному слову английского языка, как правило, ставится в соответствие несколько слов русского языка и наоборот.
Проекция на первую компоненту Пр1{(x;y)} формирует область определения Х0, где Х0Х, а на вторую компоненту Пр2{(x;y)}- область значений Y0, где Y0Y.
Область определения соответствия может быть задана на прямом произведении множеств Х, т.е. i=1n Хi=Хn.
В этом случае
Q={(x1;x2;...;xn;y)|xiX;yY}XnY
q:XnY.
Каждому соответствию q может быть найдено обратное соответствие q-1. Для этого достаточно поменять местами компоненты пары соответствия, т.е.
Q-1={(y;x)|xX;yY}YX;
Q-1={(y;x1;x2;...xn)| xiXi;yY}YXn.
Для двух соответствий q1:XY и q2:YZ можно найти их композицию, т.е. сформировать новое соответствие q=(q1q2):XZ при условии, что элементы области значений первого соответствия есть элементы области определения второго соответствия: {(x;z)|xX; zZ; Пр2{(x;y)|xX; yY}=Пр1{(y;z)|yY; zZ}}.
Например, если Х={1;3;5}, Y={2;4;6}, Z={7;9} и
для q1:XY имеем Q1={(1;2);(1;4);(3;4);(5;6)}(XY),
для q2:YZ имеем Q2={(2;9);(4;7);(4;9);(6;7)}(YZ), то
для q:XZ имеем Q={(1;9);(1;7);(3;7);(3;9);(5;7)}(XZ).
Итак, основной отличительной способностью соответствия является то, что |{y}xi|>1.
Отображения.Соответствие, когда каждому прообразу найдется единственный образ, но не наоборот, называют отображением. То есть отличительной особенностью отображения является условие |{y}xi|=1.
Форма записи отображения не отличается от записи соответствия. Однако множество пар отображения обозначают другим символом. Например,
Н={(x;y)|xX, yY}(XY).
Правило отображения также удобно представлять в операторной форме:
h:XY, где h -оператор отображения.
Проекция на первую компоненту Пр1{(x;y)} формирует область определения Х0, где Х0Х, а на вторую компоненту Пр2{(x;y)}- область значений Y0, где Y0Y.
Для отображения, область определения которого задана прямым произведением Хn, множество пар отображения и оператор отображения имеют следующий вид:
Н={(x1;x2;...;xn;y)|xiX;yY}XnY,
h: ХnY.
Каждому отображению h может быть найдено обратное отображение h-1.
Н-1={(y;x)|xX;yY}YX;
Н-1={(y;x1;x2;...xn)| xiXi;yY}YXn.
Для двух отображений h1:XY и h2:YZ можно найти их композицию, т.е. сформировать новое отображение h=(h1h2):XZ при условии, что элементы области значений первого отображение есть элементы области определения второго отображения: {(x;z)|xX; zZ; Пр2{(x;y)|xX; yY}=Пр1{(y;z)|yY; zZ}}.
В математике часто отображение называют функцией и обозначают символом f. В этом случае оператор функции есть f:XY или f:XnY.
Часто вместо такой записи используют запись:
y=f(x), где xX, yY или
y=f(x1;x2;...;xn), где (x1;x2;...;xn)Xn, yY, для которых элементы (х) или (x1;x2;...;xn) называют аргументами функции или ее независимыми переменными, y -значением функции.
При этом, если для каждого значения xX или (x1;x2;...;xn)Xnимеется один элемент yY, то функция называется всюду определенной, в противном случае -частично определенной.
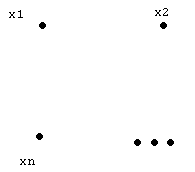
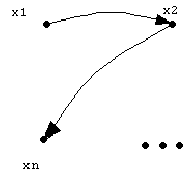
Если представить два множества Х и Y в прямоугольной системе координат (см. рис.1), то узлы прямоугольной решетки есть элементы прямого произведения (x;y)=(XY). Подмножество, ограниченное линией на рис. 1а), не является функцией, т.к. для х4есть два значения y2и y3; подмножество, ограниченное линией на рис. 1б), является всюду определенной функцией, т.к. каждому xiX соответствует единственное значение yY; подмножество, ограниченное линией на рис. 1в), является частично определенной функцией, т.к. для х3нет значения yY.
 Рис.
1. Графики функцийy=f(x).
Рис.
1. Графики функцийy=f(x).
Функцию называют операцией (operation), если ее аргументы и значения принадлежат одному множеству, т.е. f:XnХ. Аргументы операции называют операндами (operand). Количество операндов определяет местность или арность операции. Например, есть одноместные (или унарные) операции - f(x), двухместные (или бинарные) операции - f(x1;x2), трехместные (или тернарные) операции - f(x1;x2;x3) и т.д.. Однако наибольшее значение и применение имеют унарные и бинарные операции.
Арность операции и тип данных, используемых в качестве операндов и получаемых в результате исполнения операций, определяют тип операции. Для формальной записи операций используют различные схемы: префиксную, инфиксную и постфиксную.
При префиксной записи на первом месте указывается символ, знак, последовательность букв или слово, обозначающие операцию, затем в круглых скобках операнды, разделенные запятой, затем после символа “:-” значение результата исполнения операции, т.е.
а) для унарной операции: operation(operand):-result;
б) для бинарной операции: operation(operand, operand):-result.
При инфиксной записи в круглых скобках записывают последовательно первый операнд, операцию, второй операнд.
При постфиксной записи в начале в круглых скобках перечисляют операнды, а затем указывают символ операции.
Ниже приведены некоторые наиболее типичные функции для различных форм записи:
а) fln(x)=ln(x);
б) f+(x1;x2)=(x1+x2)=(x1;x2)f+
в) f*(x1;x2)=(x1x2)=(x1;x2)f*
г) fexp(x1;x2)=x1x2=(x1;x2)fexp
Для исполнения вычислительных процедур на компьютерах простейшие операнды и результаты операций принадлежат типам INTEGER, REAL.
Частным случаем функции является функция, значения которой определены на множестве {“истина”, “ложь”} или {0;1}. Такая функция называется логической или предикатом (PREDICATE)и для опознания такой функции по тексту ее принято обозначать Р(х) или Р(x1;x2) или Р(x1;x2;...;xn). При формальной записи предикатов необходимо указывать их арность и тип данных, используемых в качестве операндов.
Например, если на множестве целых чисел (INTEGER) задать предикаты:
Р21(х1):-”быть простым числом”;
Р12(x1;x2):-”х1больше х2”;
Р42(x1;x2):-”имеет общий делитель”
Р33(x1;x2;x3):- ”х3есть сумма x1и х2”, где верхний индекс у предиката означает его арность, а нижний порядковый номер предиката, то для x1=3, х2=4 и х3=7 будут получены следующие результаты:
Р21(3)=“истина”; Р12(3;4)=“ложь”; Р42(3;4)=“ложь”; Р33(3;4;7)=“истина”.
|
h |
Iy |
Ix1 |
Ix2 |
... |
Ixn |
|
|
y1 |
x11 |
x12 |
... |
x1n |
|
|
y2 |
x22 |
x22 |
... |
x2n |
|
|
y3 |
x31 |
x32 |
... |
x3n |
|
|
... |
... |
... |
... |
... |
|
|
ym |
xm1 |
xm2 |
... |
xmn |
При исследовании отображения на компьютере информацию об отображении удобнее представлять в виде h:YXn, т.е. записывать первый элемент кортежа из области значений отображения, а остальные-из области определения отображения. В этом случае отображение удобно задать в виде таблицы, каждый столбец которой имеет имя соответствующей компоненты кортежа отображения-Ixi, а каждая строка имеет отличие по значению y. В таблице 1 приведен один из возможных способов задания отображения на компьютере. Можно еще раз повторить, что число столбцов таблицы определяется длиной кортежа отображения, а число строк - мощностью формируемого множества отображения.
Отношения.Отображение, заданное между двумя или несколькими элементами одного множества Х, называют отношением. Например, между объектами математической природы такими отношениями могут быть “быть равным”, “быть большим”, “быть неравным” и т.п.. Все множество отношений между числами может быть {=;; <;}, а между объектами “нематематической” природы такими отношениями могут быть: “быть родственником”, “быть соседом”, “находиться рядом с ...”, “быть частью” и т.п.
Формальная запись отношения не отличается от записи для отображений, если принять вместо Y множество Х. Множество пар отношений обозначают символом R. Например,
R={(x1;x2)|x1,2X}X2;
R={(x1;x2;...;xn+1)|xiX}XnX=Хn+1.
Правила отношений также удобно представить в операторной форме:
r:XX или
r: XnX.
Упорядоченные последовательности (x1;x2;...;xn+1) также называют кортежами, а его элементы - компонентами.
Если (n+1)=1, то отношение называют унарным или одноместным. Такое отношение выделяет в множестве подмножество, удовлетворяющее заданному свойству.
Задание отношение r(x) равносильно заданию предиката Р1(х) на области определения. Например, на множестве целых чисел можно задать предикат Р1(х):- “быть четным числом”. В результате будет сформировано множество R(x)={2;4;6;8;...}, где хZ.
Если (n+1)=2, то отношение называют бинарным или двухместным. Такое отношение позволяет сравнить или упорядочить попарно элементы заданного множества. Для математических объектов это могут быть отношения: r1(x1;x2):-” x1 больше x2”, r2(x1;x2):-” x1равен x2”, r3(x1;x2):-” x1меньше x2”, r4(x1;x2):-” имеют общий делитель” и др.
Правило rj(x1;x2) позволяет формировать подмножества Rj(x1;x2) опираясь на вычисление предиката: Р12(x1;x2):-” x1 больше x2”, Р22(x1;x2):-” x1равен x2”, Р32(x1;x2):-” x1меньше x2”, Р42(x1;x2):-” имеют общий делитель”.
Например, на множестве целых чисел Z эти отношения сформируют следующие подмножества:
R1(x1;x2)={(10;6);(8;5);(3;1);...}ZZ;
R2(x1;x2)={(10;10);(8;8);(5;5);(3;3);...}ZZ;
R3(x1;x2)={(6;10);(5;8);(3;%);(1;3);...}ZZ;
R4(x1;x2)={(10;2);(10;5);(8;4);(6;3);...}ZZ.
Если (n+1)=3, то отношение называют тернарным или трехместным, если равно 4, то четырехместным и т.д.. Наибольшее распространение имеют бинарные отношения в связи с удобством их описания.
Каждому отношению rможет быть найдено обратное отношениеr-1, когда для данногоr(xi;xj) существует r-1(xj;xi).
Для двух отношений r1:XX иr2:XX, заданных на одном и том же множествеX, всегда можно найти их композицию, т.е.r=(r1r2):XX, при условии, что существуют такие элементыxkX, которые принадлежат отношению R1(xj;xk) и отношениюR2(xk;xj)и формируют отношениеR(xi;xj).
Отношения можно задавать перечислением всех его элементов, т.е. формированием списков, или с помощью матриц. При матричном описании бинарного отношения удобно воспользоваться квадратной матрицей (ХХ), строки и столбцы которой есть элементы множества Х, а на пересечении i-ой строки и j-го столбца ставят знак “1”, если предикат Р2(xi;xj)=“истина” и знак “0”, если предикат Р2(xi;xj)=”ложь”, т.е.
{
1, если (xi;xj)R;
r(i;j) =
0, если (xi;xj)R.
Например, для множества целых чисел Z и отношения r4(x1;x2) матрица выделена в таблице 2 прямоугольными скобками[ ].
Таблица 2.
2
3
4
5
6
8
10 2
1
0
1
0
1
1
1 3
0
1
0
0
1
0
0 4
1
0
1
0
1
1
1 5
0
0
0
1
0
0
1 6
1
1
1
0
1
1
1 8
1
0
1
0
1
1
1
1
0
1
1
1
1
1



 r4
r4

 10
10
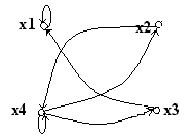
При графическом представлении отношения все элементы множества Х изображаются точками на плоскости листа и называются вершинами графа, а отношения между i-ым и j-ым элементами множества Х-линиями, которые называют ребрами ( или дугами) графа. В целом фигура, полученная на плоскости листа, называется графом. На рис.2 представлен граф для заданного множества целых чисел и отношения r4(xi;xj).
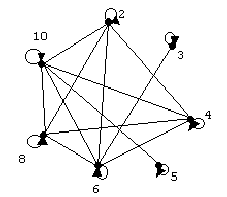
Рис. 2. Граф отношения r4(xi;xj) для Х={2;3;4;5;6;8;10}.
Свойства отношений.
Анализ различных бинарных отношений позволяет выделить наиболее характерные свойства, что необходимо для классификации всего множества отношений. Такими свойствами являются: рефликсивность, симметричность и транзитивность.
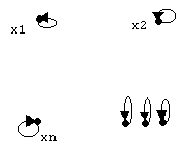
Бинарное отношение рефликсивно,если для любого хiимеем r(xi;xi)=1, т.е. отношение имеет значение “истины” при применении к одному элементу хi; такими отношениями являются “быть равным”, “быть похожим”, “быть изоморфным”, “быть эквивалентным” и т.п.; при матричном задании такого отношения это означает, что на главной диагонали матрицы находятся только “1”, а при графическом представлении - петли при каждой вершине графа(см. рис.3а)).
Бинарное отношение антирефлексивно,если для любого хiимеем r(xi;xi)=0, т.е. отношение имеет значение “ложь” применительно к одному элементу хi; такими отношениями являются “быть больше”, “быть меньше”, “быть родителем” и т.п.; при матричном задании такого отношения это означает, что на главной диагонали матрицы находятся только “0”, а при графическом представлении -отсутствие петель при каждой вершине графа(см. рис.3б)).
Бинарное отношение симметрично,если для любой пары (xi;xj) имеем r(xi;xj)=r(xj;xi)=1; это могут быть такие отношения: “быть похожим”, “быть эквивалентным”, “быть родственником” и т.п.; при матричном задании такого отношения это означает симметричное расположение “1” относительно главной диагонали, при графическом представлении - отсутствие стрелок на линиях, соединяющих вершины xi и xj, или их наличия, но в обе стороны(см. рис.3в)).
Бинарное отношение антисимметрично,если для любой пары (xi;xj) при ij имеем r(xi;xj)r(xj;xi), а при i=j r(xi;xi)=1; такими отношениями являются “быть больше или равным”, “быть меньше или равным” и т.п.; при матричном задании такого отношения это означает несимметричное расположение “1” относительно главной диагонали, но наличие их на главной диагонали, при графическом представлении - наличие стрелок на линиях, соединяющих вершины xi и xj и наличие петель у вершин графа (см. рис.3г)).
Бинарное отношение асимметрично,если для любой пары (xi;xj) имеем r(xi;xj)r(xj;xi); такими отношениями являются “быть больше”, “быть меньше”, “быть родителем” и т.п.; при матричном задании такого отношения это означает только несимметричное расположение “1” относительно главной диагонали и наличие только “0” на ней, а при графическом представлении -наличие стрелок на линиях, соединяющих вершины xi и xj и отсутствие петель у вершин графа (см. рис.2д)).
Следует обратить внимание, что антисимметричное отношение отличается от асимметричного только наличием “1” на главной диагонали или наличием петель у вершин графа.
Бинарное отношение транзитивно,если для любых трех элементов xi,xj,xkимеем r(xi;xj)=1 только при условии r(xi;xk)=1 и r(xk;xj)=1; такими отношениями являются “быть больше”, “быть меньше”, “быть родственником” и т.п.; при матричном представлении это означает, что если r(xi;xk)=1 и r(xk;xj)=1, то это же отношение можно установить между вершинами xi и xj через промежуточную вершину xk, т.е. найти r(xi;xj)=1; при графическом представлении -наличие пути из вершины xi в вершину xjчерез промежуточную вершину xk, используя ребра (xi;xk) и (xk;xj) (см. рис.3е)).
а) r
x1
x2
...
xn
1
*
*
* x2
*
1
*
* ...
*
*
1
* xn
*
*
*
1
в) r
x1
x2
...
xn
*
1
*
1 x2
1
*
*
* ...
*
*
*
* xn
1
*
*
*
д) r
x1
x2
...
xn
0
1
*
1 x2
*
0
*
* ...
*
*
0
* xn
*
*
*
0
б) r
x1
x2
...
xn
0
*
*
* x2
*
0
*
* ...
*
*
0
* xn
*
*
*
0
е) r
x1
x2
...
xn
*
1
*
* x2
*
*
*
1 ...
*
*
*
* xn
*
*
*
*
г) r
x1
x2
...
xn
1
1
*
1 x2
*
1
*
* ...
*
*
1
* xn
*
*
*
1



 x1
x1





 x1
x1





 x1
x1





 x1
x1





 x1
x1





 x1
x1


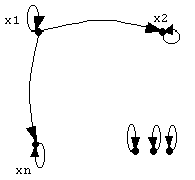
Рис. 3. Матрицы и графы, раскрывающие свойства отношений.
Контрольный вопросы и задачи.
1. Дано множество Х={x1;x2;...;x6} и Y={y1;y2;..;y4} и элементы прямого произведения этих множеств {(x1;y2);(x2;y1);(x2;y2);(x4;y2);(x4;y4)}. Определите области отправления и прибытия, определения и значений. Что это: соответствие, отображение, отношение?
2. Найти область определения и область значений для отображения:
а) h={(х;y)|Р(х;y):-”x2+4y2=1”}
б) h={(х;y)|Р(х;y):-”y0; yx; x+y1”}
в) h={(х;y)|Р(х;y):-”0x2; 0y1”}
3. Какими свойствами обладают отношения “быть больше”, “быть больше или равным”, “быть родственником”, “быть отцом”?
4. Найти геометрическую интерпретацию следующим выражениям прямого произведения множеств:
а) h={((a;b); (c;d))|a;b;c;dN};
б) h={((a;b); (a;b))|a;bN}.
5. Доказать, что если A, B, C и D не пусты, то
а) ACBD, если AB, CD;
б) ACBD, если A=B, C=D;
6. Найти обратное отображение для заданных отображений:
а) h={(х;y)|Р(х;y):-”x делит y и x,yN”};
б) h={(х;y)|Р(х;y):-”2х больше или равно 3y и x,yN”};
7. Найти композицию отношений =(1*2):
h1={(х;z)|Р(х;z):-”2x3z и x,zN”};
h2={(z;y)|Р(z;y):-”2z3y и z,yN”}.
1.4. Типы отношений и грани на множествах.
Свойства отношений позволяют классифицировать множество отношений на типы. Наиболее изученными являются отношения эквиваленции и отношения порядка. Отношение эквиваленции позволяют разбить заданное множество элементов на непересекающиеся подмножества, а отношение порядка -установить порядок между элементами заданного множества.
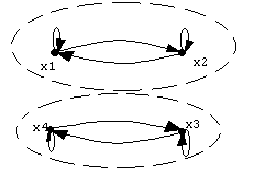
Отношение эквиваленции.Бинарное отношениеR(XX), удовлетворяющее условиям рефлексивности, симметричности, транзитивности называют отношением эквиваленции. Такими отношениями могут быть: “быть равным”, “быть похожим”, “быть одинаковым”, “быть родственником” и т.п.. Отношение эквиваленции принято обозначать знаком r~(xi;xj) или ~(xi;xj). Используя отношение эквиваленции, можно формировать классы эквиваленции K(x) по заданному образцу хв виде подмножеств Хмножества Х, т.е. K(x)=Х={xi| r~(xi;x)=1, xi, xX}X.
Два различных класса эквиваленции не имеют общих элементов множества Х, т.к. в противном случае они сформировали бы один общий класс эквиваленции. Представление множества Х в виде попарно различных классов эквиваленции K(x1), K(x2), ..., K(xт) позволяет формировать разбиение множества Х на подмножества, т.е. Х={ Х1; Х2; ...; Хn}, где ХiХ.
а) r~
x1 x2 x3 x4
1 1 0 0
1 1 0 0 x3
0 0 1 1
0 0 1 1



 x1
x1
x2

 x4
x4
б) r~
x1 x2 x3 x4
1 1 1 1 x2
1 1 1 1 x3
1 1 1 1
1 1 1 1



 x1
x1

 x4
x4
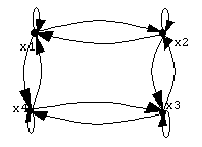
в) r~
x1 x2 x3 x4
1 0 0 0
0 1 0 0
0 0 1 1
0 0 1 1



 x1
x1
x2
x3

 x4
x4
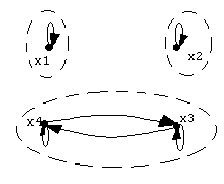
Рис. 4. Отношение эквиваленции.
Отношение порядка.Бинарные отношенияR(XX), удовлетворяющие условиям рефлексивности, антисимметричности и транзитивности называют отношением порядка. Такими отношениями являются “быть не больше”, “быть не меньше”, “быть не старше” и т.п.. Отношение порядка принято обозначать для элементов множества r(xi;xj) или(xi;xj), а для множеств- r(Xi;Xj) или(Xi;Xj). Использование отношения порядка на одном множестве Х позволяет упорядочить элементы этого множества, т.е., рассматривая отношение на каждой паре элементов множества, устанавливать частичный порядок на всём множествеX. Примерами частично упорядоченных множеств являются множество целых чисел с заданным отношением порядка, т.е. {1;2;3...}, множество действительных чисел, в том числе положительных и отрицательных, счетные множества нематематических объектов, упорядоченные по значениям индексов, т.е. Х1, Х2, ..., счетные множества букв и символов, упорядоченные алфавитом, множество подмножеств универсального множества с отношением включения(Хi, Хj) и т.п. На рис. 5а)дан пример частичного порядка.
Отношение строго порядка.Бинарное отношениеR(XX), удовлетворяющее условиям антирефлексивности, асимметричности и транзитивности называют отношением строго порядка. Такими отношениями могут быть: “быть больше”, “быть меньше”, “быть частью”, “быть подчиненным” и т.п.. Использование отношения строго порядка формирует линейную упорядоченность элементов множества Х. Для обозначения отношения строгого порядка приняты символы: между элементами множества - r<(xi;xj) или <(xi;xj), между множествами - r(Xi;Xj) или(Xi;Xj). На рис. 5б) дан пример отношения строгого порядка.
а) r
x1 x2 x3 x4
1 1 1 1 x2
0 1 1 1 x3
0 0 1 1
0 0 0 1
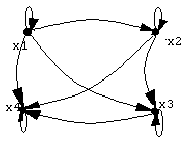



 x1
x1

 x4
x4
б) r
x1 x2 x3 x4
0 1 1 1 x2
0 0 1 1 x3
0 0 0 1
0 0 0 0



 x1
x1

 x4
x4
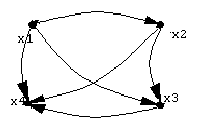
Рис. 5. Отношение порядка.
Грани на множествах.Одной из важных характеристик упорядоченного множества, т.е. множества, на котором задан частичный или строгий порядок ((xi;xj) или <(xi;xj)) или((Xi;Xj) или(Xi;Xj)), является наличие граней.
Если задано подмножество Хiстрого упорядоченного множества Х, т.е.(Хi;Х), то найдется такой элемент хХ, что для любого элемента хiХiвыполняется условие хi<х. В этом случае элемент хХ называют мажорантой множества Хi. Наименьший элемент из множества мажорант хХ называют верхней гранью множества Хiи обозначают Sup(Хi)=min{хХ}.
Если дано подмножество Хiстрого упорядоченного множества Х, т.е.(Хi;Х), то найдется такой элемент хХ, что для любого элемента хiХiвыполняется условие хi>х. В этом случае элемент хХ называют минорантой множества Хi. Наибольший элемент из множества минорант хХ называют нижней гранью множества Хiи обозначают Inf(Хi)=max{ хХ}.
При исполнении условий строго порядка, т.е. <(xi;xj) или(Хi;Хj),грани подмножества Хiне принадлежат множеству Хi, т.е. х, хХi, но принадлежат множеству Х, т.е. х, хХ.
При выполнении условий частичного порядка, т.е. (xi;xj) или(Хi, Х), грани подмножества Хiмогут принадлежать также самому подмножеству Хi. В этом случае мажоранта может быть максимальным элементом подмножества Хi, т.е. Sup(Хi)=max{хiХi}, а миноранта -минимальным элементом подмножества Хi, т.е. Inf(Хi)=min{хiХi}.
Обоснование булевой алгебры.
Если частично упорядоченное множество Х содержит только два элемента, т.е. Х={x;y} при отношении (x;y), то гранями непустого множества Х являются его собственные элементы х и y, т.е. x=InfX и y=SupX. Если элементы этого множества принимают значения только “0” или “1”, то InfX=0, SupX=1.
Операцию поиска верхней и нижней граней двухэлементного упорядоченного множества принято обозначать так: SupX=(xy), InfX=(xy), где знак ““ называют дизъюнкцией, а знак “” (““ или ““) -конъюнкцией.
Если x{0;1} и y{0;1}, то поиск граней множества Х удобно представить таблицей (см. таблицы 2,3).
Таблица 2. (xy)
y
0 1
x 0 0 1
1
1
1
Таблица 3. (xy)
y
0 1
x 0 0 0
1
0
1


Частично упорядоченное множество Х, в котором каждое двухэлементное подмножество имеет верхнюю и нижнюю грани определяет математическую структуру, которую называют решеткой. Если SupXi=1, InfXi=0 для каждого подмножества частично упорядоченного множества Х, то решетку называют булевой, в честь английского математика Дж. Буля.
Непосредственно из определения граней следуют свойства операций дизъюнкции и конъюнкции:
1) закон коммутативности: (xjxi)=(xixj) и (xjxi)=(xixj);
2) закон ассоциативности: xi(xjxk)=(xixj)xkи xi(xjxk)=(xixj)xk;
3) закон идемпотентности: (xixi)=xiи (xixi)=xi;
4) закон поглощения: xi(xixj)=xiи xi(xixj)=xi;
5) закон дистрибутивности: xi(xjxk)=(xixj)(xixk) и xi(xjxk)=(xixj)(xixk).
Обоснование алгебры множеств.
Если частично упорядоченное множество Х содержит два подмножества А и В, т.е. Х={A,B}, при условии (А;В), то гранями непустого множества Х являются A=InfX и B=SupX.
Частично упорядоченное множество Х={Х1; Х2; ...; Хn}, при условии, что любая пара подмножеств {Хi; Хj} имеют верхнюю и нижнюю грани, также является носителем математической структуры -решетки.
Операции поиска верхней и нижней граней упорядоченного множества подмножеств при условии (А;В) принято обозначать так:
SupX=(AB), InfX=(AB),
где знак ““ называют объединением множеств, а знак ““ пересечением множеств.
Непосредственно из определения граней частично упорядоченного множества подмножеств следуют свойства операций объединения и пересечения:
1) закон коммутативности: (AB)=(BA) и (AB)=(BA);
2) закон ассоциативности: A(BC)=(AB)C и A(BC)=(AB)C;
3) закон идемпотентности: AA=A и AA=A;
4) закон поглощения: A(AB)=A и A(AB)=A;
закон дистрибутивности: A(BC)=(AB)(AC) и A(BC)=(AB)(AC);
Если дано множество Х и его подмножество Хi, т.е. ХiХ, то существует множество элементов, принадлежащих множеству Х и непринадлежащих множеству Хi. Операция, обеспечивающая поиск элементов такого множества, называется дополнением множества Хiдо множества Х. Дополнение множества Хiпринято обозначать так:Хi={x|xX и xХi}.
Знак ““ означает дополнение множества. Непосредственно из определения дополнения следует основное свойство этой операции: если для ХiХ существуетХi, то ХiХi=Х и ХiХi=.
Операцию дополнения на двухэлементном множестве Х={x;y} принято обозначать так: x=y или y=x. Знак ““ равносилен знаку ““, но называется отрицанием.
Непосредственно из определения отрицания следует свойство этой операции: если для Х={x;y} существует x=y и y=x, то хy=X илихy=Х и хy=0 илиxy=0.
Если значения элементов х и y принадлежат множеству {0;1}, то имеем: 0=1, 1=0, 01=1, 10=1, 01=0, 10=0.
Контрольные вопросы и задачи.
1. Дано множество Х={1;2;3;4;5;6} и его подмножество Х1={3;4}. Укажите грани подмножества Х1.
2. Напишите множество из пяти целых чисел, эквивалентных между собой по условию “ иметь одинаковый остаток при делении на число 7”.
3. Даны множества Х0={1;2;3;4;5;6}; X1={1;2;3;4}; X2={2;3;4;5}; X3={2;3;4}; X4={3;4;5}; X5={2;3}; X6={3;4}; X7={4;5}; X8={2;4}. Сформируйте частичный порядок на множествах.
4. Пусть Х -множество всех прямых на плоскости. Являются ли эквивалентными отношения а) параллельности прямых и б) перпендикулярности прямых?
5. Дано множество Х={x|P(x):-(x=1/n), где n={1;2;...;}}. Укажите грани множества Х.
6. Найти область определения и значения для отображения
а) h={(x;y)|P(x;y):-”x;yN х делит y”};
б) h={(x;y)|P(x;y):- “x;yN и 2x3y”};
в) h={(x;y)|P(x;y):- “x;yN и х делит y только при х=y”}.
1.7. Элементы общей алгебры.
Множество Х={x1;x2;...;xn} с заданными операциямиF={F1; F2;...; Fm} формирует алгебруA=<X;F>. Множество Х называют носителем алгебры, множествоF-сигнатурой. В математической логике (см.4) будем использовать вместо понятия “сигнатура” понятие “базис”, т.к. будут сформированы несколько функционально полных алгебр, опирающихся на различные логические операции. Задания на упорядоченном множестве двух бинарных операций: объединения и пересечения (или дизъюнкции и конъюнкции) и одной унарной операции: дополнения (или отрицания) формируют общую алгебру, обеспечивающую исследование различных дискретных структур.
Итак, алгебра есть A=<X; F>.
Алгебра множеств.Непустая совокупность подмножеств универсального множестваU, замкнутая относительно операций объединения, пересечения и дополнения, формирует алгебру множестваB(U).
Таким образом алгебра множеств есть: A=< B(U);;;>, где
U-универсальное множество;
B(U)-семейство подмножеств универсального множества U, включающее в себя пустое подмножество, одноэлементные, двухэлементные и т.д. подмножества до множества, содержащего все элементы универсального множестваU;
- унарная операция дополнения любого подмножества до универсального множества U;
- бинарная операция объединения двух подмножеств множества U;
- бинарная операция пересечения двух подмножеств множества U.
Для объяснения замкнутости алгебры множеств представим универсальное множество U, опирающимся на три подмножества А, В, и С. Тогда булеан универсального множества есть:
B(U)={; {A}; {B}; {C}; {A;B}; {B;C}; {A;C}; {A;B;C}}, где {A;B} есть множество элементов подмножеств А и В; {A;C} - множество элементов подмножеств А и С; {B;C} - множество элементов подмножеств В и С; {A;B;C} - множество элементов подмножеств А, В и С, т.е. универсального множестваU.
Результаты исполнения бинарных операций (объединения и пересечения) удобно представить матрицами, строки и столбцы которых есть элементы булеана (носителя алгебры), а элементы матрицы являются результатом исполнения заданной бинарной операции (см. таблицы 4, 5). Результаты исполнения унарной операции (дополнения) удобно представить таблицей, строки которой есть элементы булеана и его дополнение (см. таблицу 6).
Таблица 4.
A
B
C
{A;B}
{A;C}
{B;C}
{A;B;C}
A
B
C
{A;B}
{A;C}
{B;C}
{A;B;C}
A
A
A
{A;B}
{A;C}
{A;B}
{A;C}
{A;B;C}
{A;B;C}
B
B
{A;B}
B
{B;C}
{A;B}
{A;B;C}
{B;C}
{A;B;C}
C
C
{A;C}
{B;C}
C
{A;B;C}
{A;C}
{B;C}
{A;B;C}
{A;B}
{A;B}
{A;B}
{A;B}
{A;B;C}
{A;B}
{A;B;C}
{A;B;C}
{A;B;C}
{A;C}
{A;C}
{A;C}
{A;B;C}
{A;C}
{A;B;C}
{A;C}
{A;B;C}
{A;B;C}
{B;C}
{B;C}
{A;B;C}
{B;C}
{B;C}
{A;B;C}
{A;B;C}
{B;C}
{A;B;C}
{A;B;C}
{A;B;C}
{A;B;C}
{A;B;C}
{A;B;C}
{A;B;C}
{A;B;C}
{A;B;C}







 {A;B;C}
{A;B;C}
Таблица 6.
{A;B;C}
{A;B;C}
A
{B;C}
B
{A;C}
C
{A;B}
{A;B}
C
{A;C}
B
{B;C}
A
{A;B;C}
Таблица 5.
A
B
C
{A;B}
{A;C}
{B;C}
{A;B;C}
A
A
A
A
A
B
B
B
B
B
C
C
C
C
C
{A;B}
A
B
{A;B}
A
B
{A;B}
{A;C}
A
C
A
{A;C}
C
{A;C}
{B;C}
B
C
B
C
{B;C}
{B;C}
A
B
C
{A;B}
{A;C}
{B;C}
{A;B;C}







 {A;B;C}
{A;B;C}
Анализ этих таблиц показывает, что результаты операций объединения, пересечения и дополнения не выходят за пределы булеана - носителя алгебры, что свидетельствует о ее замкнутости.
Рассмотрим исполнение отдельных операций над множествами А, В и С, принадлежащих универсальному множеству. Для наглядного изображения исполнения операций прямоугольником обозначают универсальное множество, а внутри него кругами изображают подмножества, принадлежащие универсальному множеству, которые называют кругами Эйлера. Заштрихованная область представляет собой результат исполнения операции. Иначе, такое изображение называют диаграммой Венна.
Объединение двух множеств А и Весть множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному множеству А или В, т.е. (АВ)={x|xA или xB}. Операторная запись объединения имеет вид:
union(A,B)={x|xA или xB}.
На рис. 6а) приведено графическое представление операции объединения двух множеств А и В.
Если В=, то АВ=А=А. Если B=U, то АВ=АU=U. Если АС и ВС, то АВС.
Операцию объединения можно распространить на произвольное число подмножеств универсального множества U. Например, если А1;А2;...;АnU, то А1А2...Аn=АiU.
Пересечение двух множеств А и Весть множество, состоящее из всех тех элементов, которые принадлежат множеству А и принадлежат множеству В, т.е. (АВ)={x|xA и xB}. Операторная запись имеет вид:
intersection(A,B)={x|xA и xB}.
На рис. 6б) приведено графическое представление операции пересечения двух множеств А и В.
Если В=, то АВ=А=. Если B=U, то АВ=АU=А. Если СА и СВ, то САВ. Если Аи В, то при АВ=множества А и В не пересекаются и не имеют общих элементов.
Операцию пересечения можно распространить на произвольное число подмножеств универсального множества. Например, если А1;А2;...;АnU, то А1А2...Аn=АiU.
Дополнение множества Адо универсального множестваUесть множество, состоящее из всех тех элементов, которые принадлежат универсальному множествуUи не принадлежат множеству А, т.е.А={x|xUи xA}. Операторная запись дополнения имеет вид: complement(A)= {x|xUи xA}.
На рис. 6в) приведено графическое представление операции дополнения для множества А. Если существует А, то справедливы следующие соотношения: АА=, АА=Uи(А)=А.
Операции дополнения, пересечения и объединения определяют две дополнительные операции: разности и симметрической разности.
Разность множеств А и Весть множество, состоящее из всех тех элементов, которые принадлежат множеству А и не принадлежат множеству В, т.е. (А\В)= {x|xА и xВ}, т.е. (А\В)=(А(В)). Операторная запись разности имеет вид:
difference(A,B)= {x|xА и xВ}.
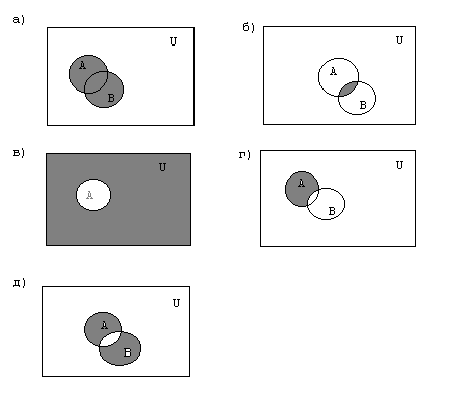
Рис. 6. Графическое изображение алгебраических операций над множествами А и В.
На рис. 6г) приведено графическое представление разности двух множеств А и В.
Симметрическая разность множеств А и Весть множество, состоящее из всех тех элементов, которые принадлежат разности (А\В) или (В\А), т.е. (АВ)=(АВ)(ВА)= {x|x(A\В) или x(B\А)}. Операторная запись симметрической разности имеет вид: union(difference(A,B), difference(B,A)).
На рис. 6д) приведено графическое изображение симметрической разности двух множеств А и В.
Если (АВ)=(АВ)(ВА)=, то А=В.
Опираясь на законы алгебры множеств, можно выполнять эквивалентные преобразования алгебраических выражений на множествах, усложняя или упрощая их описание. Выражение, элементами которого являются элементы носителя алгебры и символы алгебраических операций, называют формулой F. Последовательное применение законов алгебры множеств к формуле с целью формирования минимального выражения по числу алгебраических преобразований называют стратегией преобразования формулы.
Для облегчения исполнения преобразований формул представим основные законы и правила в таблице 7.
Таблица 7. наименование
закона, правила
эквивалентные формулы
1. коммутативности
(AB)=(BA);
(AB)=(BA); 2.
ассоциативности
A(BC)=(AB)C;
A(BC)=(AB)C; 3.
дистрибутивности
3. A(BC)=(AB)(AC);
A(BC)=(AB)(AC); 4.
идемпотентности 4.
AA=A; AA=A; 5.
поглощения 5.
A(AB)=A
и A(AB)=A; 6.
противоречия 6.
А(А)=0;
А(А)=U; 7. де
Моргана 7.
(АВ)=А(В);(АВ)=А(В); 8.
свойство универсального множества 8.
АU=U;
AU=A; 9.
свойство пустого множества 9.
А=А; А=; 10.двойного
отрицания 10.(А)=А.
Рассмотрим преобразование на примере, содержащем четыре подмножества А, В, С и D универсального множества U:
Пусть F=(ABCD)(AC)(BC)(CD);
1) выполним преобразование формулы, используя закон коммутативности
F=(CABD)(CA)(CB)(CD);
2) выполним преобразование формулы, используя закон дистрибутивности
F=(CABD)(CA)(C(BD));
3) повторим использование закона дистрибутивности
F=(CABD)(C(ABD));
4) используем еще раз закон дистрибутивности
F=C((ABD)(ABD));
5) применим закон де Моргана
F=C((ABD)(ABD));
6) используем закон противоречия
F=(CU);
7) применим известные свойства универсального множества
F=C;
В результате сложное алгебраическое выражение было преобразовано к самому простому, содержащему только одно множество С. Так можно выполнять эквивалентные преобразования различных алгебраических выражений над множествами, достигая их минимального описания.
Средствами алгебры можно искать неизвестные множества. Для этого следует воспользоваться алгоритмом, позволяющим выделить искомое множество из заданного тождества или алгебраического выражения:
шаг 1: преобразовать тождество А=В к виду алгебраического уравнения, в правой части которого будет пустое множество; для этого следует воспользоваться свойством симметрической разности: если А=В, то (АВ)(ВА)=;
шаг 2: перегруппировать все элементы алгебраического уравнения так, чтобы сформировать два выражения, связанных знаком пересечения с искомым множеством или его дополнением, т.е.
((...)1Х)((...)2Х)=;
шаг 3: приравнять пустому множеству два выражения, связанных с искомым множеством Х и его дополнением Х, т.к. их объединение может быть равным пустому множеству только при равенстве каждой из составляющих объединения, т.е.
{
((...)1Х)=;
((...)2Х)=;
шаг 4: определить область включения множества Х, опираясь на свойства операции пересечения на множествах, т.е.
Х(...)1и (...)2Х откуда (...)2Х(...)1;
Например, если поставлена задача поиска множества Х, для которого задано тождество (ХМ)=N, то имеем:
шаг 1: ((XM)N)(N(XM))=;
шаг 2: ((XM)N)(NXM)=;
(XN)(MN)(NXM)=;
(XN)(MN)(XX)(NXM)=;
(XN)(X(MN))X(MN)(X(NM))=;
(X(N(MN))X(MNNM)=;
(XN)(X(MN)=;
{
NX=;
(MN)X=;
шаг 4: (MN)XN.
Так как по условию задачи (ХМ)=N, т.е. (ХМ)N и N(XM), то МN и М(N)=. Тогда (МN)=(NM), т.е. (N\M)XN. Графически решение задачи представлено на рис.7.
mM
Рис. 7. Решение задачи (ХМ)=N.


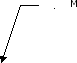 М
М

 NX
NX
Булева алгебра. Непустая совокупность элементов множества Х, принимающих значения “0” или “1”, замкнутая относительно операций дизъюнкции, конъюнкции и отрицания, формирует булеву алгебру.
Таким образом булева алгебра есть: A=<Х;;;; 0; 1>, где
Х - множество, элементы которого принимают значения “1” или “0”;
- унарная операция отрицания значения х;
- бинарная операция конъюнкции двух элементов множества Х;
- бинарная операция дизъюнкции двух элементов множества Х;
Для объяснения исполнения операций на рис., рис. 8-10 приведены результаты операций для различных значений операндов.
Дизъюнкция двух элементов х1 и х2,есть бинарная операция, принимающая значение “0” в том и только в том случае, когда оба операнда имеют значение “0”, т.е.
|
х1 |
х2 |
f(x1;x2)=(х1х2) |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Рис. 8. Дизъюнкция х1и х2.
Операторная запись дизъюнкции имеет вид: disjunct(х1;х2)= (х1х2).
На языках программирования эта операция есть логическое сложение, результатом которой является “истина” или “ложь” (“1” или “0”), и использует оператор “OR”, т.е. x1_OR_x2.
Операцию дизъюнкции можно распространить на произвольное число элементов множества X. Например, для х1; х2;...хn имеем: х1х2...хn=i=1nхi.
Конъюнкция двух элементов х1 и х2,имеющих значения “0” или “1”, есть бинарная операция, принимающая значение “1” в том и только в том случае, когда оба операнда имеют значение “1”, т.е.
|
х1 |
х2 |
f(x1;x2)=(х1х2) |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Рис. 9. Конъюнкция х1 и х2.
Операторная запись конъюнкции имеет вид: conjunct(х1; х2)= (х1х2).
На языках программирования эта операция есть логическое умножение, результатом которой является “истина” или “ложь” (“1” или “0”), и использует оператор “AND”, т.е. x1_AND_x2.
Операцию конъюнкции также можно распространить на произвольное число элементов множества X. Например, для х1; х2;...хnимме х1х2...хn=i=1nхi.
Отрицание элемента х,принимающего значения “0” или “1”, есть унарная операция, результат которой имеет значение противоположное значению операнда, т.е.
|
x |
f(x)=x |
|
0 |
1 |
|
1 |
0 |
Рис. 10. Отрицание x.
Операторная запись этой операции имеет вид: negation(x)=x.
На языках программирования для этой операции используют оператор “NOT”, а операцию записывают в префиксной форме, т.е. NOT_x.
Опираясь на законы булевой алгебры, можно выполнять эквивалентные преобразования любых алгебраических выражений, усложняя или упрощая их описание. Эквивалентные преобразования алгебраических выражений необходимы для поиска наименьшего числа вычислительных операций или достижения результатов вычислений за меньшее число шагов. Последовательное применение законов булевой алгебры, формирующее минимальное по вычислительной сложности алгебраическое выражение, называют стратегией преобразования.
Для облегчения исполнения преобразований формул булевой алгебры представим основные законы и правила в единой таблице(см. табл. 8).
Алгебраическое выражение, элементами которого являются элементы носителя алгебры и символы алгебраических операций, называют формулой F.
Таблица 8. Наименование
закона, правила Эквивалентные
формулы 1.
коммутативности
1. (х1х2)=
х2х1;
(х1х2)=
х2х1; 2.
ассоциативности
2. х1(х2х3)=
(х1х2)х3;
х1(х2х3)=
(х1х2)х3; 3.
дистрибутивности
3. х1(х2х3)=
(х1х2)(х1х3);
х1(х2х3)=
(х1х2)(х1х3); 4.идемпотентности 4.
хх=х; хх=х; 5.
поглощения 5.
х1(х1х3)=х1;
х1(х1х3)=х1; 6.
противоречия 6.
хх=1; хх=0; 7. де
Моргана 7.
(х1х2)=х1х2;(х1х2)=х1х2;
свойство “1”
8.
х1=1; х1=х; 9.
свойство “0” 9.
х0=х; х0=0; 10.
двойное отрицание 10.(х)=х.
Рассмотрим стратегию преобразования формулы F, опирающейся на три элемента х1,х2,х3, принадлежащих универсальному множеству.
F=х1х2х1(х2х1х3)( х1(х2х3)х2х3);
1) выполним преобразование по закону дистрибутивности
F=х1х2(х1х2х1х1х3)( х1(х2х3)х2х3);
2) используем закон противоречия
F=х1х2х1х2( х1(х2х3)х2х3);
3) воспользуемся законом де Моргана
F=х1х2х1х2((х1(х2х3))(х2х3));
4) повторим использование закона де Моргана
F=х1х2х1х2((х1(х2х3))(х2х3));
5) используем еще раз закон де Моргана
F=х1х2х1х2((х1((х2)х3))(х2х3));
6) используем закон двойного отрицания
F=х1х2х1х2(х1х2х3)(х2х3));
7) выполним преобразование по закону дистрибутивности
F=х1х2(х1х2х1х1х2х2х3)(х2х3);
8) используем закон идемпотентности
F=х1х2(х1х2х1х2х3)(х2х3);
9) выполним преобразование по закону дистрибутивности
F=х1х2х1х2х2х1х2х3х1х2х3х2х1х2х3х3;
10) используем закон поглощения и идемпотентности
F=х1х2х1х2х3;
Итак, сложное алгебраическое выражение в результате эквивалентных преобразований, содержит меньшее число операций для тех же трех элементов множества х1,х2,х3.
Используя накоторые дополнительные преобразования, можно еще упростить формулу F.
11) выполним преобразование по закону дистрибутивности
F=х2(х1х1х3);
12) исполним процедуру обобщенного склеивания и поглощения (подробнее см. 4.2.)
F=х2(х1х1х3х3)=х2(х1х3);
Окончательное выражение формулы имеет вид: F= х2(х1х3).
Алгебра отображений и отношений.Основным отличием этих алгебр является то, что элементами носителя алгебры являются кортежи, а подмножествами универсального множества - матрицы. Для алгебры отображений компонентами кортежа являются значения операндов или операций, т.е. числа, символы, слова и т.п., а для алгебры отношений - значения предикатов, т.е. “1” или “0” (“истина” или “ложь”).
Алгебра отображений. Пусть даны два отображения h1и h2(см. рис. 11а), 11б). Для удобства рассмотрим два совместимых отображения, т.е. имеющих одинаковую длину кортежей и одинаковые имена компонент.
При табличном представлении отображений имеем прямоугольную матрицу, число столбцов которой равно числу компонент кортежей - m, а число строк - числу кортежей отображения - n. Элементами прямоугольной матрицы являются числа, буквы, символы, слова и т.п.
Итак,
Н1={(y(1);x1(1);x2(1);...xn(1))| xi(1)X1;y(1)Y1}Y1X1n}; (см. рис.11а);
Н2={(y(2);x1(2);x2(2);...xn(2))| xi(2)X2;y(2)Y2}Y2X2n}; (см. рис.11б).
Объединение двух совместимых отображенийесть отображение, кортежи которого принадлежат первому или второму отображениям.
H=(H1H2)={(y;x1;x2;...xn)| xi(X1X2); y(Y1Y2)}.
При программировании на компьютере эту операцию записывают так: union(H1,H2) :-H.
Если все элементы двух совместимых кортежей имеют одинаковые значения, т.е. (y(1)=y(2);x1(1)=x1(2);x2(1)=x2(2);...xn(1)=xn(2)), то в результате исполнения этой операции формируется один кортеж (y;x1;x2;...xn), при различии хотя бы одной компоненты совместимых кортежей в результате исполнения этой операции формируются два кортежа (y(1);x1(1);x2(1);...xn(1)) и (y(2);x1(2);x2(2);...xn(2)). На рис. 11в) дан пример этой операции.
Пересечение двух совместимых отображенийесть отображение, кортежи которого принадлежат первому и второму отображениям.
H=(H1H2)={(y;x1;x2;...xn)| xi(X1X2); y(Y1Y2)}.
При программировании на компьютере эту операцию записывают так: intersection(H1,H2) :-H.
Если все элементы двух совместимых кортежей имеют одинаковые значения, т.е. (y(1)=y(2);x1(1)=x1(2);x2(1)=x2(2);...xn(1)=xn(2)), то в результате исполнения этой операции формируется один кортеж (y;x1;x2;...xn), при различии хотя бы одной компоненты совместимых кортежей в результате исполнения этой операции формируются пустой кортеж. На рис. 11г) дан пример этой операции.
Разность двух совместимых отображенийесть отображение, кортежи которого принадлежат первому отображению и не принадлежат второму.
H=(H1\H2)=({(y;x1;x2;...xn)| xiX1; xiХ2; yY1; yY2}
При программировании на компьютере эту операцию записывают так: dufference(H1,H2):-H.
Если все элементы двух совместимых кортежей имеют одинаковые значения, т.е. (y(1)=y(2);x1(1)=x1(2);x2(1)=x2(2);...xn(1)=xn(2)), то в результате исполнения этой операции формируется пустой кортеж, при различии хотя бы одной компоненты совместимых кортежей в результате исполнения этой операции записывается кортеж первого отображения (y(1);x1(1);x2(1);...xn(1)). На рис. 11д) дан пример исполнения этой операции.
Также может быть реализована операция симметрической разности, но невозможно сформировать дополнение отображения H в силу бесконечного множества сочетания различных компонент кортежей. Алгебра отображений формирует реляционную алгебру для управления базами данных компьютера.
Прямое произведение двух отображений h1 и h2есть отображение, кортежи которого формируются в результате присоединения слева к каждому кортежу первого отображения каждого кортежа второго отображения. В результате длина кортежа Н равна (m1+m2), где m1-длина кортежа первого отображения, m2-длина кортежа второго отображения. Число кортежей отображения Н равно (n1n2), где n1-число кортежей первого отображения, n2-число кортежей второго отображения.
Итак,
H=(H1H2)={ (y(1);x1(1);x2(1);...xn(1); y(2);x1(2);x2(2);...xn(2))| | y(Y1Y2), xi(1)X(1);xi(2)X(2)}.
При программировании на компьютере эту операцию записывают так: product(H1,H2):-H. На рис. 11е) дан пример этой операции.
а) h1
y(1)
x1(1)
x2(1) x3(1)
2
в
c 6
3
c
e 5
5
c
в 2
4
а
е 5
б) h2
y(2)
x1(2)
x2(2) x3(2)
4
а
c 3
5
c
в 2
2
в
с 6
3
с
е 5












г) (h1h2)
y
x1
x2 x3
2
в
c 6
3
c
e 5
5
с
в 2




в)
y
x1
x2
x3
2
в
c
6
3
c
e
5
4
а
е
5
4
а
с
3
5
с
в
2



 (h1h2)
(h1h2)




д) (h1\h2)
y
x1
x2
x3
[4
а
е
5]
е)
(h1h2)
y(1)
x1(1)
x2(1)
x3(1)
y(2)
x1(2)
x2(2)
x3(2)
2
в
с
6
4
а
с
3
2
в
с
6
5
с
в
2
2
в
с
6
2
в
с
6
2
в
с
6
3
с
е
5
3
с
е
5
4
а
с
3
3
с
е
5
5
с
в
2
3
с
е
5
2
в
с
6
3
с
е
5
3
с
е
5
5
с
в
2
4
а
с
3
5
с
в
2
5
с
в
2
5
с
в
2
2
в
с
6
5
с
в
2
3
с
е
5
4
а
е
5
4
в
с
3
4
а
е
5
5
с
в
2
4
а
е
5
2
в
с
6
4
а
е
5
3
с
е
5
Рис. 11 Алгебра отображений.
{






1, если (xi;xj)R;
rij =
0, если (xi;xj)R.
Такие значения элементов позволяют применить законы булевой алгебры при исполнении теоретико-множественных операций над отношениями. На рис. 12а), 12б) приведены два отношения R1иR2.
Объединение двух бинарных отношенийесть отношениеR=(R1R2), матрица которого формируется так:
rij=rij(1)rij(2).
На рис. 12в) дан пример объединения двух отношений.
Перерсечение двух бинарных отношенийесть отношениеR=(R1R2), матрица которого формируется так:
rij=rij(1)rij(2).
На рис. 12г) дан пример пересечения двух отношений.
Разность двух бинарных отношенийесть отношение R=(R1\R2), матрица которого формируется по условию
{
1, если rij(1)rij(2)и rij(1)=1;
rij=
0, если rij(1)=rij(2)или rij(1)=0.
На рис. 12д) дан пример разности двух отношений.
Дополнение отношенияможет быть найдено в виде разности между отношением заданным на всех элементах множества и данным отношениемR=1\R, матрица которого формируется в виде дополнения для каждого элемента матрицы данного отношения
{
1, если rij=0;
 rij=
rij=
0, если rij=1.
На рис. 12е) дан пример дополнения отношения R1.
г)
(R1R2)
x1
x2
x3
x4
0
0
0
0
x2
0
1
0
0
x3
0
0
1
0
0
0
0
0


 x1
x1

 x4
x4
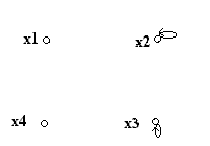
а)
R1
x1
x2
x3
x4
1
0
0
0
x2
0
1
0
1
x3
1
0
1
0
0
1
1
1
x4x3
R2
x1
x2
x3
x4
0
1
1
1
x2
1
1
0
0
x3
0
1
1
0
x4
0
0
0
0
x4x3
в)
(R1R2)
x1
x2
x3
x4
x1
1
1
1
1
x2
1
1
0
1
x3
1
1
1
0
x4
1
1
1
1













 x1
x1
 x4
x4








 x1x2
x1x2
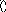








 б)
б)
 x1
x1










 x1x2
x1x2














 x1
x2
x1
x2









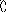






е)
R1
x1
x2
x3
x4
0
1
1
1
x2
1
0
1
0
x3
0
1
0
1
1
0
0
0
ж)
(R1R2)
x1
x2
x3
x4
x1
0
1
1
1
x2
1
1
0
0
x3
0
1
1
1
1
1
1
0



 x1
x1

 x4
x4

 x4
x4
 x4 x3
x4 x3
д)
(R1\R2)
x1
x2
x3
x4
1
0
0
0
x2
0
0
0
1
x3
1
0
0
0
0
1
1
0



 x1
x1

 x4
x4


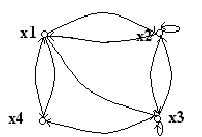
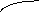
Композиция двух необязательно совместимых отношений,но имеющих обязательно одинаковые элементы на множествах Х1и Х2, есть отношение R=(R1R2), элементы которого определяются произведением булевых матриц, т.е.
rij=k=1n(rik(1)rkj(2)). На рис. 12ж) дан пример композиции отношений R1и R2.
Прямое произведение двух отношенийR1иR2есть отношение
R={((xi(1);xk(2)); (xl(1);xj(2)))|xi,xlX1, xk,xjX2}, элементы которого имеют следующие значения
{
1, если (xi(1),xl(1))=1 и (xk(2),xj(2))=1;
((xi(1),xk(2)); (xl(1),xj(2 )))=
0, если (xi(1),xl(1))=0 или (xk(2),xj(2))=0.
Прямое произведение на отношении также формирует принципиально новый математический объект.
На рис. 13б),приведена матрица прямого произведения двух отношений. Для удобства описания прямого произведения отношений в таблице 13а) приведены идентификаторы прямого произведения (X1X2), которое формирует имена строк и столбцов матрицыR.
а)
идентиф.
номер
(xi(1),xj(2))
01
(x1(1),x1(2))
02
(x1(1),x2(2))
03
(x1(1),x3(2))
04
(x1(1),x4(2))
05
(x2(1),x1(2))
06
(x2(1),x2(2))
07
(x2(1),x3(2))
08
(x2(1),x4(2))
09
(x3(1),x1(2))
10
(x3(1),x2(2))
11
(x3(1),x3(2))
12
(x3(1),x4(2))
13
(x4(1),x1(2))
14
(x4(1),x2(2))
15
(x4(1),x3(2))
16
(x4(1),x4(2))
Рис. 13а). Идентификатор (xi(1);xj(2)) X1X2.
б) (R1R2)
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
01
0
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
02
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
03
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
04
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
05
0
0
0
0
0
1
1
1
0
0
0
0
0
1
1
1
06
0
0
0
0
1
1
0
0
0
0
0
0
1
1
0
0
07
0
0
0
0
0
1
1
0
0
0
0
0
0
1
1
0
08
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
09
0
1
1
1
0
0
0
0
0
1
1
1
0
0
0
0
10
1
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
11
0
1
1
0
0
0
0
0
0
1
1
0
0
0
0
0
12
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
13
0
0
0
0
0
1
1
1
0
1
1
1
0
1
1
1
14
0
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
15
0
0
0
0
0
1
1
0
0
1
1
0
0
1
1
0
16
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Рис.13. Прямое произведение отношений
R1иR2.
Контрольные вопросы и задачи.
1. Приняв множество первых 20 натуральных чисел в качестве универсального множества, записать следующие подмножества: А-множество четных чисел, В-множество нечетных чисел, С- множество квадратов чисел, D-множество простых чисел. Для множеств А, В, С и D найти результаты следующих операций: (АВ); (АВ); (АС); (АD); C\A; C\D; (CD).
Почему AB0; AC=0; (AB)\C=0.
2. Докажите тождества:
а) (AB)(CD)=(AC)(BC)(AD)(BD);
б) (AB)=AB;
в) A(AB)=A;
г) (A\(A\B)=AB);
д) (AB)=A(B\A);
е) (AB)(AB)=A.
3. Найти неизвестное множество:
а)
{
(AX)=(BX);
(AX)=(CX).
б) AX=B;
в) A\X=B.
4. Докажите тождества:
а) (х1х2)(х1х3)(х2х4)(х3х4)=х1х4х2х3;
б) (х1х2)(х2х3)(х3х1)(х3х4)=(х1х2)(х2х3)(х3х1);
в) х1х2х3х1х2х3х1х2х3х1х2х3= х2;
г) х1х2х3х4х1х2х4х1х3х4=х1х4;
д) х1х2х3х1х2х3х1х2х3х1х2х3= х1х3х1х2х2х3;
е) х1х2х3х1х2х3х1х2= х1;
ж) ( х1х2)=х1х2;
з) х1х1х2=х1;
и) х1х2х3=(х1х2)(х1х3).
h2
y(2)
x1(2)
x2(2)
x3(2)
a
3
c
1
b
2
в
2
c
1
a
3
d
1
c
1
h1
y(1)
x1(1)
x2(1)
x3(1)
а
1
c
3
b
2
b
2
с
3
a
1
d
1
c
1












R1
x1(1)
x2(1)
x3(1)
x4(1)
1
0
0
1
x2(1)
0
1
1
0
x3(1)
0
1
1
0
1
0
0
1



 x1(1)
x1(1)

 x4(1)
x4(1)
R2
x1(2)
x2(2)
x3(2)
x4(2)
0
1
0
1
x2(2)
1
0
1
0
x3(2)
0
1
0
1
1
0
1
0



 x1(2)
x1(2)

 x4(2)
x4(2)
